二叉排序树的基本算法实现

二叉排序树的基本算法实现

实验目的：
    用二叉链表存储方式存储二叉排序树，并实现以下相关算法
    1、创建二叉排序树
    2、在二叉排序树上实现查询、插入和删除算法
    3、对二叉排序树进行中序遍历以判断目标2是否完成

实验代码如下：

#include 
#include 
using namespace std;

#define ENDFLAG -1
#define OK 1
#define ERROR 0
#define OVERFLOW -2
#define MAXSIZE 100

typedef int KeyType;
typedef int InfoType;
typedef int Status;

typedef struct  {					//二叉排序树的二叉链表存储表示
	KeyType key;					//关键字项
	InfoType otherinfo;				//其他数据项
} ElemType; 						//每个节点的数据域的类型

typedef struct BSTNode {
	ElemType data;					//每个节点的数据域包括关键字项和其他数据项
	struct BSTNode *lchild,*rchild; //左右孩子指针
} BSTNode,*BSTree;
BSTree q, p;


typedef BSTree SElemType;

typedef struct { 						//定义顺序栈
	SElemType *base;
	SElemType *top;
	int stacksize;
} SqStack;
SqStack S;

Status InitStack(SqStack &S) {
	S.base = new SElemType[MAXSIZE];
	if(!S.base) exit(OVERFLOW);
	S.top = S.base;
	S.stacksize = MAXSIZE;
	return OK;
}
Status Push(SqStack &S, SElemType e) { //入栈
	if(S.top - S.base == S.stacksize)  //判断栈满
		return ERROR;
	*S.top++ = e;                     //元素e压入栈顶，栈顶指针上移一位;
	return OK;
}
Status Pop(SqStack &S, SElemType &e) { //出栈
	if(S.top == S.base)   return ERROR;
	e = *--S.top;
	return OK;
}
SElemType GetTop(SqStack S) { 			//取栈顶元素
	if(S.top != S.base)   return *(S.top - 1);
}
Status StackEmpty(SqStack &S) {
	if(S.top - S.base == 0)    return OK;
	else return ERROR;
}

void InsertBST(BSTree &T, ElemType e) {//二叉排序树的插入
//当二叉排序树T中不存在关键字e.key的数据元素时,则插入该元素
	BSTree s;
	if (!T) {						//找到插入位置,递归结束
		s = new BSTNode;			//生成新节点*S
		s->data = e;				//新节点*S的数据域置为e
		s->lchild = s->rchild = NULL;//新节点*S作为叶子节点
		T = s;						//把新节点*S链接到已找到的插入位置
	} else if (e.key<T->data.key) 
		InsertBST(T->lchild, e);	//将*S插入左子树
	else if (e.key>T->data.key)
		InsertBST(T->rchild, e);	//将*S插入右子树
}


void CreatBST(BSTree &T) {			//创建二叉排序树
//依次读入一个关键字为key的节点，将此节点插入二叉排序树T中
	ElemType e;
	T=NULL;							//将二叉排序树初始化为空树
	cin>>e.key;
	while (e.key != ENDFLAG) {		//ENDFLAG为自定义常量,作为输入结束的标志 ,我的是-1
		InsertBST(T, e);			//将此节点插入二叉排序树T中
		cin>>e.key;
	}
}

void DeleteBST1(BSTree &T,KeyType key) {//二叉排序树的删除
//从二叉排序树T中删除关键字等于key的节点
	BSTree p,f;
	p = T;
	f = NULL;//初始化
	/*------下面的while循环从根开始查找关键字等于key的节点*p------*/
	while(p) {
		if(p->data.key == key) break;
		f = p;
		if(p->data.key > key) p = p->lchild;
		else {
			p = p->rchild;
		}
	}
	if(!p) return;

	/*------考虑3种情况实现p所指子树内部的处理:*p左右子树均不为空、无右子树、无左子树------*/
//当被删除的节点既有左子树,又有右子树,以其左子树中的最大值结点替换之，然后再删除该结点
	if((p->lchild) && (p->rchild)) {
		BSTree s;
		q = p;
		s = p->lchild;
		while(s->rchild) {
			q = s;
			s = s->rchild;
		}
		p->data = s->data;
		if(q != p) q->rchild = s->lchild;
		else {
			q->lchild  = s->lchild;
		}
		delete s;
		return;
	}

	else if(!p->rchild) {
		q = p;
		p = p->lchild ;
	} else if(!p->lchild) {
		q = p;
		p = p->rchild;
	}

	/*------将p所指的子树挂接到其双亲节点*f相应的位置------*/
	if(!f) T = p;
	else if(q == f->lchild) f->lchild = p;
	else f->rchild = p;
	delete q;
}

void DeleteBST2(BSTree &T,KeyType key) {//二叉排序树的删除
//从二叉排序树T中删除关键字等于key的节点
	BSTree p,f;
	p = T;
	f = NULL;//初始化
	/*------下面的while循环从根开始查找关键字等于key的节点*p------*/
	while(p) {
		if(p->data.key == key) break;
		f = p;
		if(p->data.key > key) p = p->lchild;
		else {
			p = p->rchild;
		}
	}
	if(!p) return;

	/*------考虑3种情况实现p所指子树内部的处理:*p左右子树均不为空、无右子树、无左子树------*/
//当被删除的节点既有左子树,又有右子树,以其右子树中的最大值结点替换之，然后再删除该结点
	if((p->lchild) && (p->rchild)) {
		BSTree s;
		q = p;
		s = p->rchild;
		while(s->lchild) {
			q = s;
			s = s->lchild;
		}
		p->data = s->data;
		if(q != p) q->lchild = s->rchild;
		else {
			q->rchild  = s->rchild;
		}
		delete s;
		return;
	}

	else if(!p->rchild) {
		q = p;
		p = p->lchild ;
	} else if(!p->lchild) {
		q = p;
		p = p->rchild;
	}

	/*------将p所指的子树挂接到其双亲节点*f相应的位置------*/
	if(!f) T = p;
	else if(q == f->lchild) f->lchild = p;
	else f->rchild = p;
	delete q;
}

BSTree SearchBST(BSTree T, KeyType key) {//二叉排序树的查找
	if (!T||key==T->data.key) return T;
	else if ( key< T->data.key )
		return SearchBST(T->lchild, key);
	else  return SearchBST(T->rchild, key);
}


void InOrderTraverse(BSTree T) { 	//非递归中序遍历
	BSTree p,q;
	InitStack(S);					//初始化栈
	p = T;
	q = new BSTNode;
	while(p || !StackEmpty(S)) {
		if(p) { 					//p非空
			Push(S, p);				//根指针进栈
			p = p->lchild;			//根指针进栈，遍历左子树
		} else { 					//p为空
			Pop(S, q);				//退栈
			cout << " " << q->data.key;	//访问根结点
			p = q->rchild;			//遍历右子树
		}
	}
}

int main() {

	BSTree T = NULL;
	ElemType e;
	int key,i;

	printf("请创建二叉排序树(输入-1结束): \n");
	CreatBST(T);
	printf("非递归中序遍历所创建的二叉排序树：\n");
	InOrderTraverse(T);

	printf("\n请输入需要查找的关键字：\n");
	scanf("%d",&key);
	if (!SearchBST(T,key)) {
		printf("您要找的关键字不存在！\n");
	} else {
		T = SearchBST(T,key);
		printf("您要找的关键字在二叉排序树中！\n");
	}

	printf("\n请输入需要插入的关键字: \n") ;
	scanf("%d",&e);
	InsertBST(T,e);
	printf("\n非递归中序遍历验证插入操作：\n");
	InOrderTraverse(T);


	while (true) {
		printf("\n请选择您所用的删除方法(请选择1或2,选择0退出):  ");
		scanf("%d",&i);

		switch(i) {
			case 0:
				return 0;
			case 1:
				printf("\n请输入需要删除的关键字(删除方法一)：\n");
				scanf("%d",&key);
				DeleteBST1(T,key);
				printf("\n非递归中序遍历验证删除操作：\n");
				InOrderTraverse(T);
				break;
			case 2:
				printf("\n请输入需要删除的关键字(删除方法二)：\n");
				scanf("%d",&key);
				DeleteBST2(T,key);
				printf("\n非递归中序遍历验证删除操作：\n");
				InOrderTraverse(T);
				break;
			default:
				printf("您输入了错误的指令！");
				break;
		}
	}
	
	return 0;
}

运行结果如下：
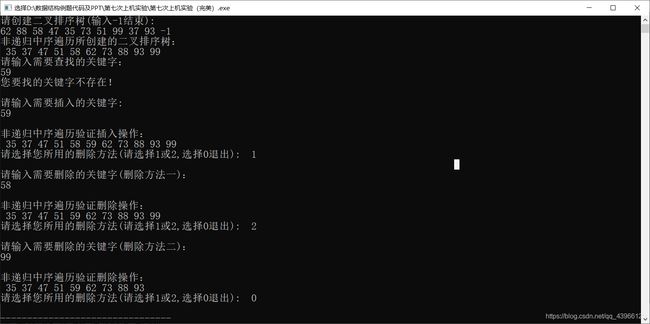这里创建二叉排序树，在查找的时候，如果是查找不存在的那个数，那么插入时候一点问题也没有，但是如果查找存在的那个数，运用插入算法的时候会有一点小问题，所以这个是一个小BUG,然后在输入的时候查找不存在的那个数，并且插入那个数就行了。
关于删除算法，我这里写了两个，具体在算法注释里面都有，可以选择使用！