Tensorflow学习笔记----梯度下降

一．梯度（Gradient）的理解：

• 导数：一维函数沿x轴的变动率；
  偏微分：二维函数沿各个方向的变动率；
  梯度：三维及以上函数沿各个方向的变动率，当函数沿某一方向的值突然变动很大时，它在这个方向的此数梯度就会大；

可以利用梯度来寻找函数的最小值，即寻找全局最优，方法就是从任一点出发，然后重复朝着梯度的反方向（变小的方向？）前进（有可能找到的是局部最小即极小）；

• 公式：θt+1 = θt - a * ∂θt
  使用tensorflow计算梯度：
  With tf.GradientTape() as tape:
  [w_grad] = tape.gradient(loss,[w])

二．激活函数（Activation Function）及其梯度：

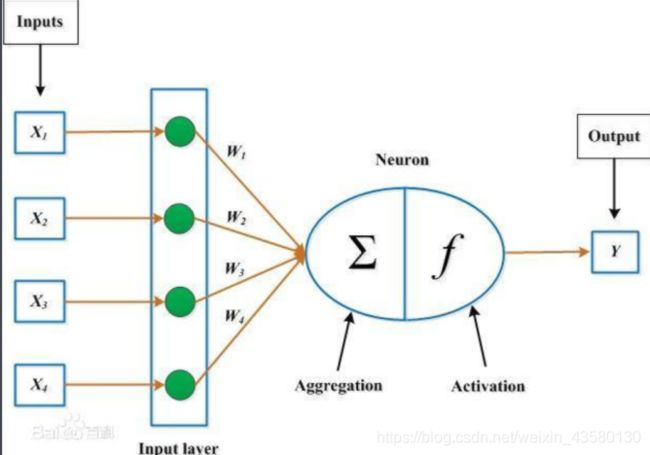
对于所有的输入加权求和后，还要在激活函数中判断是否到达阈值，到达阈值（被激活）才能进行输出，且输出的信号值是固定的。引入激活函数是为了增加神经网络模型的非线性。常见的激活函数有Sigmoid函数，tanh函数，Relu函数，ELU函数等。这类函数是不可导的，所以不能像普通函数那样求梯度。

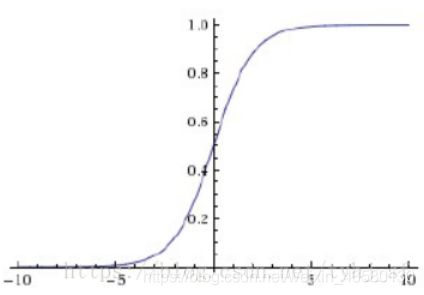
Sigmoid函数/Logistic：，函数值被压缩在(0,1)，可求导；缺点就是容易造成梯度弥散现象。

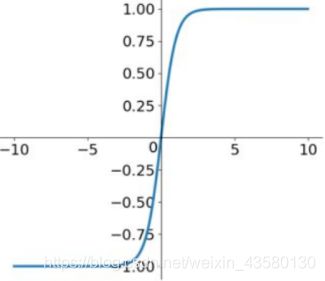
Tanh函数： = 2sigmoid(2x)-1，范围在(-1,1)

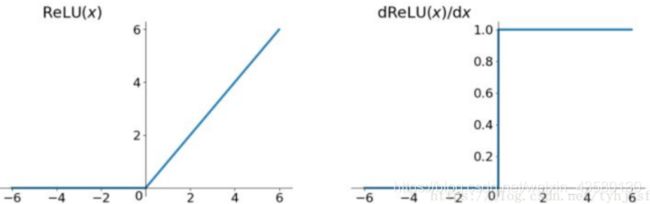
ReLU函数（Rectified Linear Unit，整流线性单元）：，是现在深度学习用得最多的，因为它的倒数非常简单，不会出现梯度弥散和梯度爆炸的情况，而且计算速度很快。

三．损失（Loss）函数及其梯度

MSE（Mean Squared Error）：均方差 = Σ(y-y’)2；y’=wx+b。常用于回归问题
求导：d loss/dθ = 2Σ(y-y’) * d y’/dθ

#MSE Gradient
x = tf.random.normal([2,4]) #输入：2个simple:[b,4]
w = tf.random.normal([4,3]) #把4维降到3维==>最终分为3类
b = tf.zeros([3])
y = tf.constant([2,0])

with tf.GradientTape() as tape:
    tape.watch([w,b])
    prob = tf.nn.softmax(x@w+b,axis=1)
    loss = tf.reduce_mean(tf.losses.MSE(tf.one_hot(y,depth=3),prob))

grads = tape.gradient(loss,[w,b])
print(grads[0])
# tf.Tensor(
# [[-0.05369104  0.07968411 -0.02599307]
#  [-0.0535683  -0.0183023   0.0718706 ]
#  [-0.0789809   0.02822249  0.05075841]
#  [ 0.08340039 -0.03885455 -0.04454585]], shape=(4, 3), dtype=float32)

Cross Entropy Loss：交叉熵误差，常用于分类算法；交叉熵描述了两个概率分布之间的距离；

• 常用Softmax回归将神经网络前向传播得到的结果变成概率分布，softmax常用于多分类过程中，它将多个神经元的输出，归一化到( 0, 1) 区间内，因此Softmax的输出可以看成概率，从而来进行多分类。以下为Softmax的公式：
  

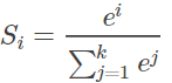
#Crossentropy Gradient
x = tf.random.normal([2,4]) #输入：2个样本:[b,4]
w = tf.random.normal([4,3]) #把4维降到3维==>最终分为3类
b = tf.zeros([3])
y = tf.constant([2,0])

with tf.GradientTape() as tape:
    tape.watch([w,b])
    logits = x@w+b
    loss = tf.reduce_mean(tf.losses.categorical_crossentropy(tf.one_hot(y,depth=3),logits,from_logits=True))

grads = tape.gradient(loss,[w,b])
print(grads)
# [
# array([[ 0.06907368, -0.15770483,  0.08863113],
#        [-0.9181866 ,  0.9900556 , -0.07186895],
#        [ 0.45953235, -0.42940605, -0.03012631],
#        [ 0.46102345, -0.36747423, -0.09354922]], dtype=float32)>, ]
print(grads[0])
# tf.Tensor([-0.44427255  0.6398322  -0.1955596 ], shape=(3,), dtype=float32)

四．单输出感知机及其梯度

单层感知机预测值：y = Σxi * yi + b；它使用Sigmoid来当做激活函数，结点只有输入层、权值、求和、Sigmoid、输出；下面的O表示输出，Oj表示第j个输出，t为目标值。

• Loss = 1/2 (O10 - t)2，对其j层求导：(O0 - t) O0 (1 - O0)xj0；

#单输出感知机梯度
x = tf.random.normal([1,3])
w = tf.ones([3,1])
b = tf.ones([1])
y = tf.constant([1])

with tf.GradientTape() as tape:
    tape.watch([w,b])
    logits = tf.sigmoid(x@w+b)
    loss = tf.reduce_mean(tf.losses.MSE(y,logits))  #本身输出已经在0~1，所以不需要再one_hot encoding

grads = tape.gradient(loss,[w,b])
print(grads)
# [
# array([[ 0.16532627],
#        [ 0.11723918],
#        [-0.23324907]], dtype=float32)>, ]

五．多输出感知机及其梯度

与单输出类似，不过有m个加权和，m个输出

• Loss = 1/2 Σ(O1i - ti)2；对其j层求导：(Ok - tk) Ok (1 - Ok)xj0；

#多输出感知机梯度
x = tf.random.normal([2,4])
w = tf.ones([4,3])
b = tf.ones([3])
y = tf.constant([2,0])

with tf.GradientTape() as tape:
    tape.watch([w,b])
    prob = tf.nn.softmax(x@w+b,axis=1)
    loss = tf.reduce_mean(tf.losses.MSE(tf.one_hot(y,depth=3),prob))

grads = tape.gradient(loss,[w,b])
print(grads[0])