例1:LeetCode 第 70 题:Climbing Stairs
传送门:英文网址:70. Climbing Stairs ,中文网址:70. 爬楼梯 。
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2 输出: 2 解释: 有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶示例 2:
输入: 3 输出: 3 解释: 有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
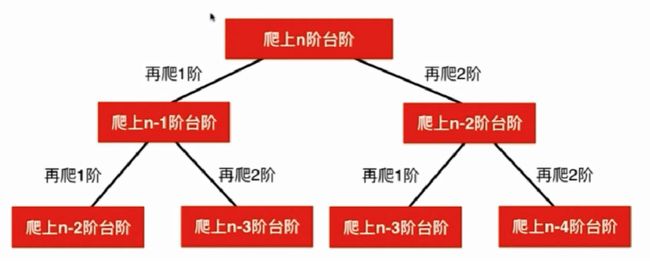
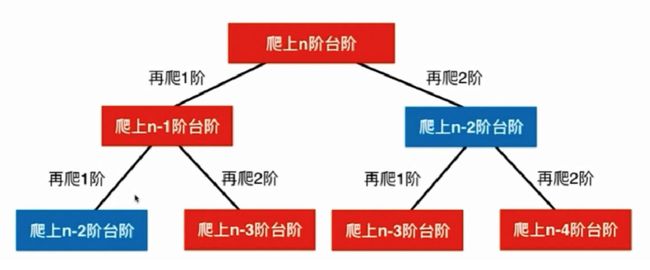
分析:分析问题过程中,我们发现这是一个递归问题,进而发现这个递归结构中存在许多重叠子问题,所以既可以使用记忆化搜索(从上到下),也可以使用动态规划(从下到上)来解决。最终我们发现,这个问题其实和斐波那契数列问题完全等价。我们可以画出这个问题的递归结构图。
我们可以发现:1、该图是一个树形结构图;2、有重叠子问题。
递归实现
Python 代码1:不合格的递归版本,存在大量重复计算
class Solution:
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
if n == 0:
return 1
if n == 1:
return 1
return self.climbStairs(n - 1) + self.climbStairs(n - 2)
Java 代码:不合格的递归版本,存在大量重复计算
public class Solution {
public int climbingStairs(int n) {
if (n <= 0) {
return 1;
}
int res = climbinng(n);
return res;
}
private int climbinng(int n) {
if (n == 1) {
return 1;
}
if (n == 2) { // 方法1:一个台阶,一个台阶;方法2:一次上两个台阶
return 2;
}
// 接下来就是看图说话了(乘法计数原理)
return climbinng(n - 1) * 1 + climbinng(n - 2) * 1;
}
}
说明:这一版代码有大量的“重叠子问题”,我们应该加上缓存。
使用记忆化搜索
Python 代码2:加入“缓存”的递归实现
class Solution:
memo = None
def _climbStairs(self, n):
if Solution.memo[n] != -1:
return Solution.memo[n]
if n == 0:
return 1
if n == 1:
return 1
Solution.memo[n] = self._climbStairs(n - 1) + self._climbStairs(n - 2)
return Solution.memo[n]
def climbStairs(self, n):
Solution.memo = [-1] * (n + 1)
return self._climbStairs(n)
Java 代码:加入“缓存”的递归实现
public class Solution {
private int[] memory;
public int climbingStairs(int n) {
if (n <= 0) {
return 1;
}
memory = new int[n + 1];
for (int i = 0; i < n + 1; i++) {
memory[i] = -1;
}
int res = climbinng(n);
return res;
}
private int climbinng(int n) {
if (n == 1) {
return 1;
}
if (n == 2) { // 方法1:一个台阶,一个台阶;方法2:一次上两个台阶
return 2;
}
// 接下来就是看图说话了(乘法计数原理)
if (memory[n] == -1) {
memory[n] = climbinng(n - 1) * 1 + climbinng(n - 2) * 1;
}
return memory[n];
}
}
说明:递归的代码写起来比较繁琐,我们可以用于思考。另一种写法就是“自底向上”,即“动态规划”。“动态规划”的代码是比较简洁的。
使用动态规划
在“记忆化搜索”的基础上,写出的动态规划版本。
思考过程:爬 0 个台阶,有 1 种爬法;
爬 个台阶,有 种爬法;
爬 个台阶,有 种爬法;
爬 个台阶,;
爬 个台阶,;
爬 个台阶,;
爬 个台阶,;
以此类推。其中, 表示首先爬 个台阶的所有不同爬法,然后再爬 个台阶的不同爬法。
Python 代码:
class Solution:
def climbStairs(self, n):
if n == 0:
return 1
memo = [-1] * (n + 1)
memo[0] = 1
memo[1] = 1
for i in range(2, n + 1):
memo[i] = memo[i - 1] + memo[i - 2]
return memo[n]
Java 代码:
public class Solution2 {
public int climbingStairs(int n) {
if (n <= 0) {
return 1;
}
if (n == 1) {
return 2;
}
int[] memory = new int[n + 1];
for (int i = 0; i < n + 1; i++) {
memory[i] = -1;
}
for (int i = 2; i < n + 1; i++) {
memory[i] = memory[i - 1] + memory[i - 2];
}
return memory[n + 1];
}
}
练习
练习1:LeetCode 第 120 题: 三角形最小路径和
传送门:三角形最小路径和。
给定一个三角形,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
例如,给定三角形:
[ [2], [3,4], [6,5,7], [4,1,8,3] ]自顶向下的最小路径和为
11(即,2 + 3 + 5 + 1 = 11)。说明:
如果你可以只使用 O(n) 的额外空间(n 为三角形的总行数)来解决这个问题,那么你的算法会很加分。
思路:关键的地方在于“从上到下”和“从下到上”思考的路径不同,导致解答的复杂程度不同。
1、“从上到下”:最边上的点只能从最边上的点走过来;
2、“从下到上”:每一点都有两个孩子:左孩子和右孩子,可以少掉很多讨论。
Python 代码:没有记忆化搜索的版本,有很多重叠子问题,讨论比较复杂
class Solution:
def __init__(self):
self.triangle = None
def __pass_way(self, i, j):
'''
:param i: 表示第几层
:param j: 表示第几个索引,j<=i
:return:
'''
if i == 0:
return self.triangle[0][0]
res = float("inf")
if j == 0:
res = min(res, self.triangle[i][j] + self.__pass_way(i - 1, 0))
elif j == i:
res = min(res, self.triangle[i][j] + self.__pass_way(i - 1, j - 1))
else:
res = min(res, self.triangle[i][j] + self.__pass_way(i - 1, j - 1),
self.triangle[i][j] + self.__pass_way(i - 1, j))
return res
def minimumTotal(self, triangle):
"""
:type triangle: List[List[int]]
:rtype: int
"""
self.triangle = triangle
res = float("inf")
n = len(self.triangle)
for i in range(n):
res = min(res, self.__pass_way(n - 1, i))
return res
Python 代码:加入了“缓存”,实现记忆化搜索
class Solution:
def __init__(self):
self.triangle = None
self.memo = []
def __pass_way(self, i, j):
"""
:param i: 表示第几层
:param j: 表示第几个索引,j<=i
:return:
"""
if i == 0:
return self.triangle[0][0]
# 如果有缓存,就读缓存的内容
if self.memo[i][j] is not None:
return self.memo[i][j]
res = float("inf")
# 最左边的点,
if j == 0:
res = min(res, self.triangle[i][j] + self.__pass_way(i - 1, 0))
elif j == i:
res = min(res, self.triangle[i][j] + self.__pass_way(i - 1, j - 1))
else:
res = min(res, self.triangle[i][j] + self.__pass_way(i - 1, j - 1),
self.triangle[i][j] + self.__pass_way(i - 1, j))
self.memo[i][j] = res
return self.memo[i][j]
def minimumTotal(self, triangle):
"""
:type triangle: List[List[int]]
:rtype: int
"""
self.triangle = triangle
res = float("inf")
n = len(self.triangle)
for i in range(1, n + 1):
self.memo.append([None] * i)
for i in range(n):
res = min(res, self.__pass_way(n - 1, i))
return res
if __name__ == '__main__':
triangle = [[2], [3, 4], [6, 5, 7], [4, 1, 8, 3]]
s = Solution()
res = s.minimumTotal(triangle)
print(res)
有了以上的分析,弄清楚递归结构,发现重叠子问题,我们还可以“自下而上”地用动态规划,代码看起来不会那么臃肿。
Python 代码3:动态规划
class Solution:
def minimumTotal(self, triangle):
"""
:type triangle: List[List[int]]
:rtype: int
"""
rows = len(triangle)
for i in range(1, rows):
current_cols = len(triangle[i])
for j in range(current_cols):
if j == 0:
triangle[i][j] = triangle[i][j] + triangle[i - 1][0]
elif j == (current_cols - 1):
triangle[i][j] = triangle[i][j] + triangle[i - 1][j - 1]
else:
triangle[i][j] = min(triangle[i][j] + triangle[i - 1][j - 1],
triangle[i][j] + triangle[i - 1][j])
return min(triangle[rows - 1])
Python 代码3:动态规划
class Solution:
def minimumTotal(self, triangle):
"""
:type triangle: List[List[int]]
:rtype: int
"""
if len(triangle) == 0:
return 0
# 这里要多留一个位置,防止数组越界
dp = [0] * (len(triangle) + 1)
for i in range(len(triangle) - 1, -1, -1):
for j in range(i + 1):
# 【关键】自底向上,每个元素都有左右孩子,就相当于在最后一行加上一行 0
dp[j] = triangle[i][j] + min(dp[j], dp[j + 1])
print(dp)
return dp[0]
if __name__ == '__main__':
triangle = [[2], [3, 4], [6, 5, 7], [4, 1, 8, 3]]
# triangle = [[-10]]
s = Solution()
res = s.minimumTotal(triangle)
print(res)
下面是在 LeetCode 讨论区看到的一个写法,更简洁。
Python 代码:推荐
class Solution:
def minimumTotal(self, triangle):
"""
:type triangle: List[List[int]]
:rtype: int
"""
l = len(triangle)
if l == 0:
return 0
dp = triangle[-1]
for i in range(l - 2, -1, -1):
for j in range(len(triangle[i])):
dp[j] = min(dp[j], dp[j + 1]) + triangle[i][j]
return dp[0]
练习2:LeetCode 第 64 题:最小路径和
传送门:英文网址:64. Minimum Path Sum ,中文网址:64. 最小路径和 。
给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例:
输入: [ [1,3,1], [1,5,1], [4,2,1] ] 输出: 7 解释: 因为路径 1→3→1→1→1 的总和最小。
思路:每一步只能左移或者下移。题目中给出了 grid 非负整数,可以保证走得越长,sum 的值越大;只能向右走或者向下走,保证了在非负整数矩阵的情况下,sum 的最小值存在。在分析清楚以后,我们可以直接在 grid 矩阵上原地修改,直接给出动态规划的解法,十分简单,逻辑也很清晰,核心代码不超过 10 行。
Python 代码:状态很好定义,题目中问什么,状态就定义成什么:dp[i][j]。
class Solution(object):
def minPathSum(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
m = len(grid)
if m == 0:
return 0
n = len(grid[0])
for col in range(1, n):
# 第 0 行特殊处理,不要忘记了
grid[0][col] += grid[0][col - 1]
for row in range(1, m):
grid[row][0] += grid[row - 1][0]
for col in range(1, n):
grid[row][col] += min(grid[row - 1][col], grid[row][col - 1])
return grid[-1][-1]
Python 代码:与上面的写法一模一样
class Solution:
def minPathSum(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
rows = len(grid)
cols = len(grid[0])
for j in range(1, cols):
grid[0][j] = grid[0][j] + grid[0][j - 1]
for i in range(1, rows):
for j in range(cols):
if j == 0:
grid[i][j] = grid[i][j] + grid[i - 1][j]
else:
grid[i][j] = min(grid[i][j] + grid[i - 1][j], grid[i][j] + grid[i][j - 1])
return grid[rows - 1][cols - 1]
(本节完)