CTR深度学习模型之 DIN(Deep Interest Network) 的理解与例子
在电商领域,每个用户都有丰富的历史行为数据,这些数据具有如下特点:
-
多样性(Diversity):用户可能对多种商品感兴趣,例如手机、衣服。
-
局部激活(Local Activation):用户是否点击新商品,仅仅取决于历史行为中与新商品相关度高的部分数据。
如何从中捕获特征对CTR预估模型非常重要。论文 《Deep Interest Network for Click-Through Rate Prediction 提出了深度兴趣网络 Deep Interest Network,以下简称 DIN 模型,设计了类似 attention 的网络结构来激活历史行为数据中与候选广告相关度高的行为,即:增大与目标广告相关性高的历史行为权重。
模型解读
基准模型
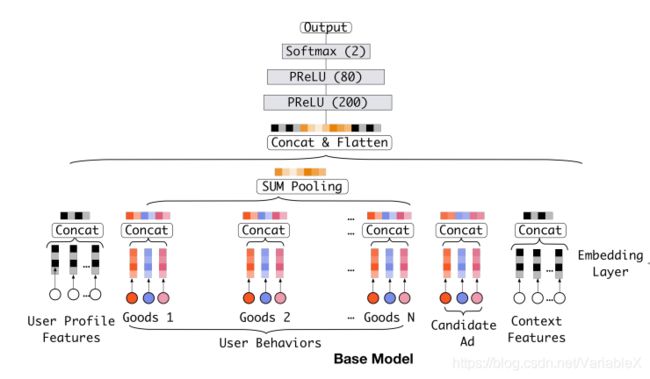
论文并没有直接讲解DIN模型,而是先介绍了基准模型的结构:
此模型主要功能是将输入的用户特征、行为特征、候选广告以及上下文特征转换成 embedding,然后将这些 embedding 拼接在一起用几个全连接层完成点击率的预测。这里面有几个需要注意的细节:
1,用户行为序列的长度一般是不同的,所以为了能够将不同序列长度的embedding 向量转换成相同的大小,一种思路是将所有的 embedding 向量进行 sum pooling,即对所有 embedding 向量求和,得到一个固定大小的向量,作为全连接层的输入。
2,直接对行为的 embedding 向量求和,会损失很多信息,即:无法捕捉到候选广告与历史行为信息中的局部相关性。
DIN模型
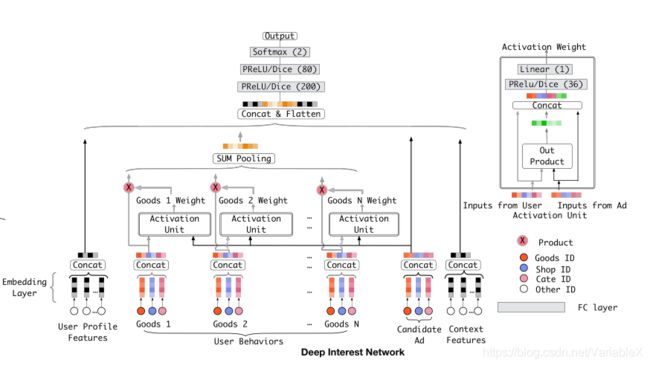
于是,在论文中又提出了改进后的模型: DIN,网络结构如下图:
与基准模型相比,最大的区别在于:引入了与 attention 机制功能相似的 Activation Unit 用于根据候选广告计算历史行为的权重。
如果用 { e 1 , e 2 , . . . , e H e_1, e_2, ... , e_H e1,e2,...,eH} 表示用户 U 对 H 个商品行为 embedding 向量, v A v_A vA 表示候选广告的向量,那么用户 U 对广告 A 的兴趣向量 v U ( A ) v_U(A) vU(A) 可以用下面的公式计算:
v U ( A ) = f ( v A , e 1 , e 2 , . . . , e H ) = ∑ j = 1 H a ( e j , v A ) e j = ∑ j = 1 H w j e j v_U(A) = f(v_A,e_1,e_2,...,e_H)=\sum_{j=1}^Ha(e_j,v_A)e_j=\sum_{j=1}^Hw_je_j vU(A)=f(vA,e1,e2,...,eH)=j=1∑Ha(ej,vA)ej=j=1∑Hwjej
其中, a ( ⋅ ) a(\cdot) a(⋅) 本质上是一个前馈神经网络,用于计算 e j e_j ej 的权重 w j w_j wj。在计算权重时,需要将 e j e_j ej 与 v A v_A vA 作为下图 Activation Unit 的输入,最终得到的输出就是权值。
如果历史行为中某个商品 e j e_j ej 与候选广告商品 v A v_A vA 相似度高,那么在使用 SUM Pooling 计算 v U ( A ) v_U(A) vU(A) 时,相似度高的商品的权重也应该高一些。从公式可以看出,引入了 Activation Unit 之后,不同的候选广告,用户的兴趣向量也会有所不同。
需要注意的是,与 attention 不同,权值 w 不需要保证的和为1。
训练技巧
Dice 激活函数
PReLU 可以看作是 ReLU 的改版,计算方法为:
f ( s ) = { s i f s > 0 α s i f s ≤ 0 = p ( s ) ⋅ s + ( 1 − p ( s ) ) ⋅ α s \begin{aligned} f(s) & =\left\{ \begin{array}{l} s \;\;\qquad if\quad s>0 \\ \alpha s \qquad if\quad s \le 0 \end{array} \right. \\ & = p(s) \cdot s + (1-p(s))\cdot\alpha s \end{aligned} f(s)={sifs>0αsifs≤0=p(s)⋅s+(1−p(s))⋅αs
无论是 ReLU 或者是 PReLU 突变点都是0。而论文认为突变点的选择应该依赖于数据,于是基于 PReLU 提出了 Dice 激活函数:
f ( s ) = p ( s ) ⋅ s + ( 1 − p ( s ) ) ⋅ α s p ( s ) = 1 1 + e − s − E [ s ] V a r [ s ] + ϵ f(s)=p(s) \cdot s+(1-p(s)) \cdot \alpha s\\ p(s)=\frac{1}{1+e^{-\frac{s-E[s]}{\sqrt{V a r[s]+\epsilon}}}} f(s)=p(s)⋅s+(1−p(s))⋅αsp(s)=1+e−Var[s]+ϵs−E[s]1
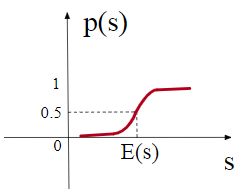
其中 E [ s ] , V a r [ s ] E[s], Var[s] E[s],Var[s] 分别是每个 mini-batch 数据的均值与方差, ϵ \epsilon ϵ 取 1 0 − 8 10^{-8} 10−8 。于是, p ( s ) p(s) p(s) 函数的图像如下:
这样的激活函数能够适应不同分布的输入数据,整体表现要优于 PReLU。
自适应正则化
在使用例如 l 2 l_2 l2 这样的传统正则化方法时,每一个 mini-batch 正则化项的计算都需要所有的参数的参与,在参数数量庞大的情况下,这个计算消耗太大了。于是论文提出了一种正则化方法,只需要对在每个 mini-batch 中出现的参数进行计算。
回顾 DIN 模型,发现绝大多数参数出现在 embedding 层,令:
W ∈ R D × K W \in R ^{D \times K} W∈RD×K
表示整个 embedding 层的参数,其中 D 是嵌入维度,K 是特征个数。则正则化项的计算公式如下:
L 2 ( W ) ≈ ∑ j = 1 K ∑ m = 1 B α m j n j ∣ ∣ w j ∣ ∣ 2 2 L_2(W) \approx \sum_{j=1}^K \sum_{m=1}^B \frac{\alpha_{mj}}{n_j}||w_j||_2^2 L2(W)≈j=1∑Km=1∑Bnjαmj∣∣wj∣∣22
其中, α m j \alpha_{mj} αmj 表示特征 j 是否出现在 mini-batch 样本 B 中, n j n_j nj 表示样本 j 在 B 中的出现次数, w j w_j wj 则是第 j 个嵌入向量。整个公式的核心思想是出现的频率越大,正则化的强度越小。
GAUC 评估指标
GAUC 是 AUC 的加权平均:
G A U C = ∑ i = 1 n w i × A U C i ∑ i = 1 n w i = ∑ i = 1 n i m p i × A U C i ∑ i = 1 n i m p i \mathrm{GAUC}=\frac{\sum_{i=1}^{n} w_{i} \times \mathrm{AUC}_{i}}{\sum_{i=1}^{n} w_{i}}=\frac{\sum_{i=1}^{n} \mathrm{imp}_{i} \times \mathrm{AUC}_{i}}{\sum_{i=1}^{n} \mathrm{imp}_{i}} GAUC=∑i=1nwi∑i=1nwi×AUCi=∑i=1nimpi∑i=1nimpi×AUCi
其中:n 是用户的数量, A U C i AUC_i AUCi 表示用户 i i i 所有样本的 AUC, i m p i imp_i impi 是用户 i i i 所有样本的个数。AUC 是考虑所有样本的排名,而实际上,我们只要关注给每个用户推荐的广告的排序,因此GAUC更具有指导意义。
模型例子
例子是在 tensorflow2.0 的环境中使用了 deepctr 实现的 DIN 模型,deepctr 安装方式如下:
pip install deepctr[gpu]
在其 github 仓库中提供了一个 demo,其代码以及关键部分的注释如下:
import numpy as np
from deepctr.models import DIN
from deepctr.feature_column import SparseFeat, VarLenSparseFeat, DenseFeat,get_feature_names
def get_xy_fd():
# 对基础特征进行 embedding
feature_columns = [SparseFeat('user',vocabulary_size=3,embedding_dim=10),
SparseFeat('gender', vocabulary_size=2,embedding_dim=4),
SparseFeat('item_id', vocabulary_size=3,embedding_dim=8),
SparseFeat('cate_id', vocabulary_size=2,embedding_dim=4),
DenseFeat('pay_score', 1)]
# 指定历史行为序列对应的特征
behavior_feature_list = ["item_id", "cate_id"]
# 构造 ['item_id', 'cate_id'] 这两个属性历史序列数据的数据结构: hist_item_id, hist_cate_id
# 由于历史行为是不定长数据序列,需要用 VarLenSparseFeat 封装起来,并指定序列的最大长度为 4
# 注意,对于长度不足4的部分会用0来填充,因此 vocabulary_size 应该在原来的基础上 + 1
feature_columns += [VarLenSparseFeat(SparseFeat('hist_item_id', vocabulary_size=3 + 1,embedding_dim=8,embedding_name='item_id'), maxlen=4),
VarLenSparseFeat(SparseFeat('hist_cate_id', 2 + 1,embedding_dim=2 + 1, embedding_name='cate_id'), maxlen=4)]
# 基础特征数据
uid = np.array([0, 1, 2])
ugender = np.array([0, 1, 0])
iid = np.array([1, 2, 3])
cate_id = np.array([1, 2, 2])
pay_score = np.array([0.1, 0.2, 0.3])
# 构造历史行为序列数据
# 构造长度为 4 的 item_id 序列,不足的部分用0填充
hist_iid = np.array([[1, 2, 3, 0], [3, 2, 1, 0], [1, 2, 0, 0]])
# 构造长度为 4 的 cate_id 序列,不足的部分用0填充
hist_cate_id = np.array([[1, 2, 2, 0], [2, 2, 1, 0], [1, 2, 0, 0]])
# 构造实际的输入数据
feature_dict = {'user': uid, 'gender': ugender, 'item_id': iid, 'cate_id': cate_id,
'hist_item_id': hist_iid, 'hist_cate_id': hist_cate_id, 'pay_score': pay_score}
x = {name:feature_dict[name] for name in get_feature_names(feature_columns)}
y = np.array([1, 0, 1])
return x, y, feature_columns, behavior_feature_list
if __name__ == "__main__":
x, y, feature_columns, behavior_feature_list = get_xy_fd()
# 构造 DIN 模型
model = DIN(dnn_feature_columns=feature_columns, history_feature_list=behavior_feature_list)
model.compile('adam', 'binary_crossentropy',
metrics=['binary_crossentropy'])
history = model.fit(x, y, verbose=1, epochs=10)
DIN 模型至少需要传入两个参数,一个是 dnn_feature_columns , 用于对所有输入数据进行 embedding;另一个是 history_feature_list,用于指定历史行为序列特征的名字,例如 [“item_id”, “cate_id”]。
要特别注意的地方是:特征 f 的历史行为序列名为 hist_f 。例如要使用 ‘item_id’, ‘cate_id’ 这两个特征的历史行为序列数据,那么在构造输入数据时,其命名应该加上前缀“hist_” ,即 ‘hist_item_id’, ‘hist_cate_id’。
参考链接:
CTR预估–阿里Deep Interest Network
Deep Interest and Evolution Network for CTR
AI算法工程师手册/DIN