本文来自我的个人博客 https://www.zhangshenghai.com/posts/63466/
目前,所有的NP完全问题都没有能够在多项式时间内求解的算法,我们通常可以采用以下几种解题策略:
- 只对问题的特殊实例求解
- 用动态规划法或分支限界法求解
- 用概率算法求解
- 只求近似解
- 用启发式方法求解
本节主要讨论的是解NP完全问题的近似算法。
近似算法的性能
若一个最优化问题的最优值为,求解该问题的一个近似算法的一个近似最优解相应的目标函数值为,则将近似算法的性能比定义为:
通常情况下,该性能比是问题输入规模的一个函数,即
顶点覆盖问题的近似算法
问题描述
无向图的顶点覆盖是它的顶点集的一个子集,使得若是的一条边,则或。顶点覆盖V’的大小是它所包含的顶点个数。 下面给出一个近似比为2的算法的伪代码:
VertexSet approxVextexCover(Graph g)
{
cset = NULL;
e = g.e;
while (e != NULL)
{
从e中任取一条边(u, v);
将顶点u,v加入cset;
从e中删去与u和v相关联的边;
}
return cset;
}
算法运行过程
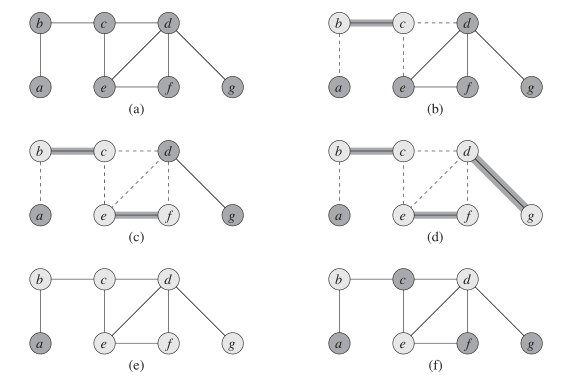
下图是《算法导论》中顶点覆盖问题近似算法的图例,说明了算法的运行过程和结果。
图(e)表示近似算法产生的近似最优顶点覆盖cset,它由顶点b,c,d,e,f,g所组成。图(f)是图G的一个最小顶点覆盖,它只含有3个顶点:b,d和e。
性能分析
假定算法选取的边集为A,则返回的顶点个数为2A。即。图G的任一顶点覆盖都至少包含A中各条边中的一个顶点,即。
则
旅行商问题的近似算法
问题描述
给定一个完全无向图,其每一边有一非负整数费用。要找出的最小费用哈密顿回路。
费用函数c往往具有三角不等式性质,即对任意的3个顶点,有:。
在费用函数不一定满足三角不等式的一般情况下,不存在具有常数性能比的解TSP问题的多项式时间近似算法,除非。换句话说,若,则对任意常数,不存在性能比为ρ的解决旅行售货员问题的多项式时间近似算法。
下面给出一个解决满足三角不等式的旅行商问题的近似算法伪代码:
APPROX-TSP-TOUR(G, c)
任意选择V中的一个顶点r,作为树根节点
调用Prim算法得到图G的最小生成树T
先序遍历T,得到顶点序列L
删除L中的重复顶点形成哈密顿环C
输出C
算法运行过程
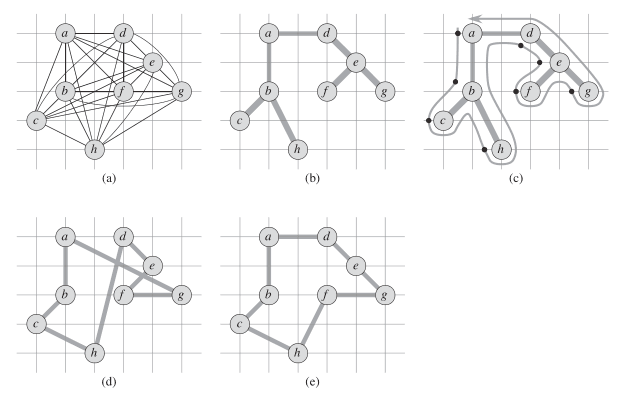
下图是APPROX-TSP-TOUR的操作过程,(a)示出了给定点的集合,(b)示出了一个最小生成树T,它是由MST-PRIM计算出来的,根为a节点,(c)是对T进行先序遍历时的顶点序列,(d)是近似算法得到的路线。
性能分析
假设是一个最优游程,如图e所示。由于我们通过删除一个游程路线中的任一边而得到一棵生成树,故最小生成树的权值是最优游程代价的一个下界,即。
假设图c中的遍历的代价为,该遍历经过了的每条边两次,则有,两式联立有。由于是从完全遍历中删除了某些顶点得到的,故有,则。
则