一文绝对让你完全弄懂信息熵、相对熵、交叉熵的意义《繁凡的深度学习笔记》第 3 章 分类问题与信息论基础（中）（DL笔记整理系列）

《繁凡的深度学习笔记》第 3 章分类问题与信息论基础 （中）（逻辑回归、信息论基础、Softmax回归）（DL笔记整理系列）

[email protected]

https://fanfansann.blog.csdn.net/

https://github.com/fanfansann/fanfan-deep-learning-note

作者：繁凡

version 1.0  2022-1-20

 

声明：

1）《繁凡的深度学习笔记》是我自学完成深度学习相关的教材、课程、论文、项目实战等内容之后，自我总结整理创作的学习笔记。写文章就图一乐，大家能看得开心，能学到些许知识，对我而言就已经足够了 ^q^ 。

2）因个人时间、能力和水平有限，本文并非由我个人完全原创，文章部分内容整理自互联网上的各种资源，引用内容标注在每章末的参考资料之中。

3）本文仅供学术交流，非商用。所以每一部分具体的参考资料并没有详细对应。如果某部分不小心侵犯了大家的利益，还望海涵，并联系博主删除，非常感谢各位为知识传播做出的贡献！

4）本人才疏学浅，整理总结的时候难免出错，还望各位前辈不吝指正，谢谢。

5）本文由我个人（ CSDN 博主 「繁凡さん」（博客） ， 知乎答主 「繁凡」（专栏）， Github 「fanfansann」（全部源码） ， 微信公众号 「繁凡的小岛来信」（文章 P D F 下载））整理创作而成，且仅发布于这四个平台，仅做交流学习使用，无任何商业用途。

6）「我希望能够创作出一本清晰易懂、可爱有趣、内容详实的深度学习笔记，而不仅仅只是知识的简单堆砌。」

7）本文《繁凡的深度学习笔记》全汇总链接：《繁凡的深度学习笔记》前言、目录大纲

8）本文的Github 地址：https://github.com/fanfansann/fanfan-deep-learning-note/ 孩子的第一个 『Github』！给我个 $\boxed{⭐\text{Starred}}$ 嘛！谢谢！！o(〃＾▽＾〃)o

9）此属 version 1.0 ，若有错误，还需继续修正与增删，还望大家多多指点。本文会随着我的深入学习不断地进行完善更新，Github 中的 P D F 版也会尽量每月进行一次更新，所以建议点赞收藏分享加关注，以便经常过来回看！

如果觉得还不错或者能对你有一点点帮助的话，请帮我给本篇文章点个赞，你的支持是我创作的最大动力！^0^

要是没人点赞的话自然就更新慢咯 >_<

《繁凡的深度学习笔记》第 3 章 分类问题与信息论基础（上）目录

第 3 章 分类问题 （逻辑回归、Softmax 回归、信息论基础）
    3.1 手写数字分类问题
      3.1.1 手写数字图片数据集
      3.1.2 构建模型
      3.1.3 误差计算
      3.1.4 非线性模型
      3.1.4 手写数字图片识别实战
         3.1.4.1 TensorFlow2.0 实现
         3.1.4.2 PyTorch 实现
    3.2 逻辑回归（Logistic Regression, LR）
      3.2.1 决策边界
      3.2.2 逻辑回归模型
      3.2.3 代价函数
      3.2.4 优化方法

《繁凡的深度学习笔记》第 3 章 分类问题与信息论基础（下）目录

    3.4 Softmax 回归
      3.4.1 Softmax 回归模型
      3.4.2 优化方法
      3.4.3 权重衰减
      3.4.4 Fashion-MNIST 数据集图片分类实战
    3.5 Softmax 回归与逻辑回归的关系
      3.5.1 Softmax 回归与逻辑回归的关系
      3.5.2 多分类问题的 Softmax 回归与 k 个二元分类器
    3.6 面试问题集锦
    3.7 参考资料

《繁凡的深度学习笔记》第 3 章（中）分类问题与信息论基础

3.3 信息论基础

信息论是一个非常庞大的学科，这里仅对机器学习中常用的简单信息论基础进行清晰易懂的简要讲解。如果对信息论感兴趣想要深入学习，请继续阅读Thomas M. Cover 的 《Elements of Information Theory》 （信息论经典之作）以及其中译本《信息论基础》，详见 我的Github 项目《繁凡的深度学习笔记》免.费深度学习书籍 。

3.3.1 信息论

  信息论是运用概率论与数理统计的方法研究信息熵、通信系统、数据传输、数据压缩等问题的应用数学学科，主要研究的是对一个信号能够提供的信息多少进行量化。信息论涉及编码、解码、发送以及尽可能简洁地处理信息或数据，主要的研究对象是关于随机变量的信息熵和信道。

3.3.1.1 自信息与信息量

  信息量（amount of information），指信息多少的量度。我们需要知道，信息是用来减少随机不确定性的东西，也即不确定性的减少。

  自信息（self-information），又译为信息本体，由克劳德 · 香农（Claude Shannon）提出，用来衡量单一事件发生时所包含的信息量多寡。任何事件都会承载着一定的信息量，包括已经发生的事件和未发生的事件，只是它们承载的信息量会有所不同。

  例如对于昨天下雨这个已知事件，因为是已经发生的事件，是既定事实，那么它的信息量就为 $0$ 。对于明天会下雨这个事件，因为未有发生，那么这个事件的信息量就大。我们可以发现信息量是一个与事件发生概率相关的概念。对于一个事件来说，它发生的概率越大，确定性越强，显然它所含有的信息量就越低。一件事情发生的概率越低，不确定性越强，它包含的信息量就越大。

  至此，信息论假设信息量它只与随机变量的概率分布有关，满足可加性等性质。

定义事件 $X=x_i$ 的自信息为
$$I\left(x_i\right)={\log }_b\frac{1}{P(x_i)}=-{\log }_{b}P\left(x_i\right)=-\log P\left(x_i\right)\text{\hspace{1em}(3.32)}$$

其中，$X$ 为随机变量，$x_i$ 为随机变量的某个取值，$P$ 为 $X$ 的概率分布： $X\sim P(X)$ ，$n$ 表示事件的个数，参数 $b$ 不同时对应的结果单位不同，在公式中可忽略。在机器学习中，用自然对数 $e$ 为底，单位为 奈特（$\mathrm{n}\mathrm{i}\mathrm{t}$），用 $2$ 为底，单位为比特（$\mathrm{b}\mathrm{i}\mathrm{t}$）。至于我们为什么会这样定义自信息，我们将在下一节 《繁凡的深度学习笔记》3.3.2 香农熵 中进行详细探讨。

我们同样可以定义事件 $X=x_i,Y=y_i$ 的联合自信息：

$$I\left(x_i,y_j\right)=\log \frac{1}{P\left(x_i,y_j\right)}\text{\hspace{1em}(3.33)}$$
如果 $X$ 与 $Y$ 相互独立，则：
$$\begin{array}{rl}I\left(x_i,y_j\right)& =\log \frac{1}{P\left(x_i\right)}+\log \frac{1}{P\left(y_i\right)}\\ & =I\left(x_i\right)+I\left(y_j\right)\end{array}\text{\hspace{1em}(3.34)}$$
直观上我们要求需要自信息满足如下的性质：

1. 连续性，即事件的自信息 $I$ 随着 $P$ 的变化连续变化。
2. 单调递减性，即发生的概率越小，确定它发生所需要的信息量越大。
3. 当 $P\to 0$ 时， $I\to \infty$ ，即确定不可能事件发生需要的信息量为无穷大。
4. 当 $P\to 1$ 时，$I\to 0$，即对确定一定会发生事件发生需要的信息量为0。
5. 独立随机变量的自信息等于各自自信息的代数和。

由此可见，信息的本质是对不确定性的消除。

3.3.2 香农熵

3.3.2.1 熵

  我们首先来介绍信息学中熵的概念。

  熵 (Entropy)，本是热力学中的概念，1948 年，克劳德 · 香农（Claude Shannon）将热力学中的熵的概念引入到信息论中，因此也被称为 信息熵 或香农熵 (Shannon Entropy)，用来衡量信息的不确定度。不准确点说，熵是用来衡量混乱程度的。越混乱，熵越大，代表不确定性越大，要弄清楚情况所需要的信息量越多。

  举个栗子，一个袋子有 $10$ 个球。如果其中有 $5$ 个红球 $5$ 个白球，这就是混乱的。如果有 $9$ 个红球和 $1$ 个白球，这就不混乱。可以理解为如果各种物品的比例相同，不同物品的概率都很大，那么我想要判断袋子里面有什么东西就比较困难，整体的信息量就很大，就会非常混乱。如果袋子仅有一种物品，那么我判断袋子里的物品就非常容易，这便是不混乱。也即一个集合里面各部分比例越均衡越混乱，各部分越两极分化越不混乱。

  那么如何使用数学来衡量混乱程度呢？ 我们显然发现当物品的总数不变的情况下，两种物品数目的乘积越大越混乱，越小越不混乱。那么我们显然就可以用这个相乘的结果来衡量数据混乱程度。既然如此，如果袋子中有多种球，我们可以将他们的概率连乘即可。

  但是我们发现连乘起来以后求导比较困难，例如对 $f(P(x))\times g(P(x))$ 进行求导我们就需要将其展开。一个显而易见的思路就是对乘积取对数将乘法变成加法，这样不仅求导更加方便，原先的单调性也没有改变。

  但是我们发现取对数以后虽然 $\log P(x)$ 是单调递增的，但是概率 $P(x)$ 不能取 $0$。我们知道概率的取值范围为 $[0,1]$，而当 $P(x)=0$ 时，此时极限是负无穷的 $\log (P(x))$ 是没有任何意义的。考虑能不能让 $0$ 乘上负无穷使其变成 $0$，于是我们就得到了衡量混乱程度的指标：$P(x)\times \log P(x)$，此 $P(x)\to 0$ 时，$P(x)\times \log P(x)=0$。此时 $P(x)$ 单调递增，$\log (P(x))$ 单调递减。相乘为单调递减。由于我们希望概率越大，不确定性也即熵的大小越小，因此我们可以取负号，至此我们就得到了香农熵的形式，同时也被香农在数学上严格证明满足信息熵三个条件的随机变量不确定性度量函数具有的唯一形式：

$$H\left(X\right)=-\sum _{i=1}^{n}P\left(x_i\right)\log P\left(x_i\right)$$

信息论之父克劳德·香农，总结出的信息熵的三条性质：

• 单调性，即发生概率越高的事件，其所携带的信息熵越低。极端案例就是“太阳从东方升起”，因为为确定事件，所以不携带任何信息量。从信息论的角度，认为这句话没有消除任何不确定性。
• 非负性，即信息熵不能为负。这个很好理解，因为负的信息，即你得知了某个信息后，却增加了不确定性是不合逻辑的。
• 累加性，即多随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度的和。

  因此我们定义事件 $X=x_i$ 的信息量 $I(x_i)=-\log P(x_i)$，此时信息量的期望就是熵，也即：

$$\begin{array}{rl}H\left(\mathrm{x}\right)& =-\sum _{i=1}^{n}P\left(x_i\right){\log }_{b}P\left(x_i\right)\\ & ={\mathbb{E}}_{\mathrm{x}\sim P}\left[I\left(x\right)\right]=-{\mathbb{E}}_{\mathrm{x}\sim P}\left[\log P\left(x\right)\right]\end{array}$$

其中 $P$ 为 $X$ 的概率质量函数，$n$ 表示事件的个数，参数 $b$ 不同时对应的结果单位不同。在机器学习中，用自然对数 $e$ 为底，单位为 奈特（$\mathrm{n}\mathrm{i}\mathrm{t}$），用 $2$ 为底，单位为比特（$\mathrm{b}\mathrm{i}\mathrm{t}$）。对于连续变量则被称为 微分熵。

一个随机变量 $X$ 的熵 $H(X)$ 的大小可以理解为事件信息量的比特数。

  这里以 $2$ 为底举个例子，对于 $4$ 分类问题，如果某个样本的真实标签是第 $4$ 类，one-hot 编码为 $[0,0,0,1]$ ，即这张图片的分类是唯一确定的，它属于第 $4$ 类的概率 $(y=4|x)=1$，不确定性为 $0$，它的熵可以简单的计算为
$$-0\times {\log }_{2}0-0\times {\log }_{2}0-0\times {\log }_{2}0-1\times {\log }_{2}1=0$$

也就是，对于确定的分布，熵为 $0$，即不确定性最低。如果它预测的概率分布是 $[0.1,0.1,0.1,0.7]$，它的熵可以计算为

$$-0.1\times {\log }_{2}0.1-0.1\times {\log }_{2}0.1-0.1\times {\log }_{2}0.1-0.7\times {\log }_{2}0.7\approx 1.356\mathrm{b}\mathrm{i}\mathrm{t}$$

  考虑随机分类器，它每个类别的预测概率是均等的：$[0.25,0.25,0.25,0.25]$，这种情况下的熵约为 $2$。

  由于 $P(i)\in [0,1],\log 2(i)\le 0$，因此熵总是大于等于 $0$。当熵取得最小值 $0$时，不确定性为 $0$。分类问题的 One-hot 编码的分布就是熵为 0 的例子。我们可以使用 math.log 来组合计算熵。

  对于 0-1 分布问题，二值随机变量的香农熵、伯努利分布熵，随机变量 $x$ 的取值为 $\{0,1\}$，此时熵的计算可以简化为
$$H\left(\mathrm{x}\right)=-P\left(x\right)\log \left(P\left(x\right)\right)-\left(1-P\left(x\right)\right)\log \left(1-P\left(x\right)\right)$$

  另一个经典的例子是：在一场赌马比赛中，有 $4$ 匹马 $\{A,B,C,D\}$ ，获胜概率分别为 $\{\frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{8}\}$，将哪一匹马获胜视为随机变量 $X$ 属于 $\{A,B,C,D\}$。假定我们需要用尽可能少的二元问题来确定随机变量 $X$ 的取值，也即我们可以给出若干个询问，每组询问只能得到两种答案：对或者错。请问最少需要通过多少个问题，来知道最后是哪匹马获得了胜利？

例如：问题 1 ：$A$ 获胜了吗？问题 2 ：$B$获胜了吗？问题 3 ：$C$ 获胜了吗？最后我们可以通过最多 $3$ 个二元问题，来确定 $X$ 的取值，也即最终是哪一匹马获得了胜利。

如果最终是 $A$ 获得胜利，也即 $X=A$ ，那么只需要问 $1$ 次（问题 1 ） 即可得到答案，$A$ 获胜的概率为 $\frac{1}{2}$。

如果最终是 $B$ 获得胜利，也即 $X=B$ ，那么需要问 $2$ 次（问题 1 以及问题 2 ），$B$ 获胜的概率为 $\frac{1}{4}$ 。

如果最终是 $C$ 获得胜利，也即 $X=C$，那么需要问 $3$ 次（问题 1，问题 2，问题 3 ），$C$ 获胜的概率为 $\frac{1}{8}$。

如果最终是 $D$ 获得胜利，也即 $X=D$，那么需要问 $3$ 次（问题 1 ，问题 2 ，问题 3 ），$D$ 获胜的概率为 $\frac{1}{8}$。

那么为确定 $X$ 取值的二元问题的数量期望次数为：

$$E(N)=\frac{1}{2}\cdot 1+\frac{1}{4}\cdot 2+\frac{1}{8}\cdot 3+\frac{1}{8}\cdot 3=\frac{7}{4}$$

那么我们带入到信息熵的公式中，选取 $\log$ 的底数为 $2$ ，即可得到：

$$H(X)=\frac{1}{2}\log (2)+\frac{1}{4}\log (4)+\frac{1}{8}\log (8)+\frac{1}{8}\log (8)=\frac{1}{2}+\frac{1}{2}+\frac{3}{8}+\frac{3}{8}=\frac{7}{4}\text{ bit }$$

  在二进制计算机中，一个比特为 $0$ 或 $1$ ，其实就代表了一个二元问题的回答。平均码长 $L(C)=\sum _{x\in X}P(x)l(x)$，其中 $P(x)$ 为概率，$l(x)$ 为码长，在计算机中，我们给哪一匹马夺冠这个事件进行编码，所需要的平均码长为 $1.75$ 个比特。

  为了尽可能减少码长，我们要给发生概率 $P(x)$ 较大的事件，分配较短的码长 $l(x)$ 。这样就可以得出霍夫曼编码的概念。

  那么 $\{A,B,C,D\}$ 四个事件，可以分别由 $\{0,10,110,111\}$ 表示，显然我们要把最短的码 $0$ 分配给发生概率最高的事件 $A$ ，以此类推。而且得到的平均码长为 $1.75$ 比特。如果我们硬要反其道而行之，给事件 $A$ 分配最长的码 $111$ ，那么平均码长就会变成 $2.625$ 比特。

  霍夫曼编码就是利用了这种大概率事件分配短码的思想，而且可以证明这种编码方式是最优的。我们可以证明：

• 为了获得信息熵为 $H(X)$ 的随机变量 $X$ 的一个样本，平均需要抛掷均匀硬币（或二元问题） $H(X)$ 次（参考猜赛马问题的案例）

• 信息熵的大小是数据压缩过程中能达到的一个临界值。

3.3.2.2 联合熵

  与联合自信息相同，我们可以定义两个随机变量 $X$ 和 $Y$ 的联合熵为：

$$\begin{array}{rl}H(X,Y)& =-\sum _{x\in X}\sum _{y\in Y}P(x,y)\log P(x,y)\\ & =-\sum _{x\in X}\sum _{y\in Y}P(x,y)\log (P(x)P(y\mid x))\\ & =-\sum _{x\in X}\sum _{y\in Y}P(x,y)\log P(x)-\sum _{x\in X}\sum _{y\in Y}P(x,y)\log P(y\mid x)\\ & =-\sum _{x\in X}P(x)\log P(x)-\sum _{x\in X}\sum _{y\in Y}P(x,y)\log P(y\mid x)\\ & =H(X)+H(Y\mid X)\end{array}$$

  在物理意义其度量了一个联合分布的随机系统的不确定度，观察了该随机系统的信息量。

  当事件 $X=A,Y=B$ 同时发生且相互独立时，有 $P(X=A,Y=B)=P(X=A)\times P(Y=B)$ ，此时信息熵

$$H(A,B)=H(A)+H(B)$$

也即当随机变量 $X,Y$ 相互独立时，有

$$H(X,Y)=H(X)+H(Y)$$

3.3.2.3 互信息

  两个随机变量 $X$ 和 $Y$ 的互信息定义为：

$$\begin{array}{rl}I(X,Y)=& \sum _{x\in X}\sum _{y\in Y}P(x,y)\log \left(\frac{P(x,y)}{P(x)\ast P(y)}\right)\\ & =\sum _{x\in X}\sum _{y\in Y}P(x,y)\log P(x,y)-\sum _{x\in X}\sum _{y\in Y}P(x,y)\log (P(x)\ast P(y))\\ & =-\sum _{x\in X}\sum _{y\in Y}P(x,y)\log P(x)-\sum _{x\in X}\sum _{y\in Y}P(x,y)\log P(y)-\left(-\sum _{x\in X}\sum _{y\in Y}P(x,y)\log P(x,y)\right)\\ & =-\sum _{x\in X}P(x)\log P(x)-\sum _{y\in Y}P(y)\log P(y)-\left(-\sum _{x\in X}\sum _{y\in Y}P(x,y)\log P(x,y)\right)\\ & =H(X)+H(Y)-H(X,Y)\\ & =H(Y)-H(Y\mid X)\\ & =H(X)-H(X\mid Y)\\ & =H(X,Y)-H(Y\mid X)-H(X\mid Y)\end{array}$$

  当 $X,Y$ 不相互独立时：
$$I(X,Y)=H(X)+H(Y)-H(X,Y)$$

  互信息代表一个随机变量包含另一个随机变量信息量的度量。其物理意义表明了两事件单独发生的信息量是有重复的。互信息度量了这种重复的信息量大小。在一个点到点通信系统中，发送端信号为 $X$ ，通过信道后，接收端接收到的信号为 $Y$ ，那么信息通过信道传递的信息量就是互信息 $I(X,Y)$。根据这个概念，香农推出了非常伟大的公式，香农公式，给出了临界通信传输速率的值，即信道容量：

$$C=B\log (1+\frac{S}{N})$$

3.3.2.4 条件熵

  两个随机变量 $X$ 和 $Y$ 的条件熵定义为：

$$\begin{array}{rl}H(Y\mid X)& =\sum _{x\in X}P(x)H(Y\mid x)=-\sum _{x\in X}P(x)\sum _{y\in Y}P(y\mid x)\log P(y\mid x)\\ & =-\sum _{x\in X}\sum _{y\in Y}P(x,y)\log \frac{P(x,y)}{P(x)}\\ & =-\sum _{x\in X}\sum _{y\in Y}P(x,y)\log P(x,y)+\sum _{x\in X}\sum _{y\in Y}P(x,y)\log P(x)\\ & =-\sum _{x\in X}\sum _{y\in Y}P(x,y)\log P(x,y)+\sum _{x\in X}P(x)\log P(x)\\ & =H(X,Y)-H(X)\end{array}$$

  条件熵度量了在已知随机变量 $X$ 的条件下随机变量 $Y$ 的不确定性，也即在 $X$ 已知的条件下，获得 $Y$ 对于整体信息量的增加情况，有：

$$\begin{array}{rl}H(X,Y)& =H(X)+H(Y\mid X)\\ & =H(Y)+H(X\mid Y)\end{array}$$

它们组成的 Venn 图如图 3.11 所示：

图 3.11 信息熵

  

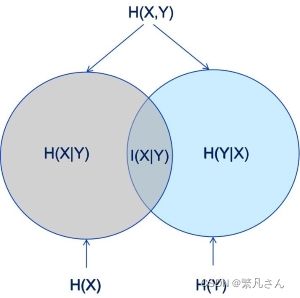
3.3.2.5 信息熵的链式法则

三个随机变量的互信息可以表示成：

$$H\left(X_1,X_2,X_3\right)=H\left(X_1\right)+H\left(X_2\mid X_1\right)+H\left(X_3\mid X_1,X_2\right)$$

则对于 $n$ 个随机变量 $X_1,\dots ,X_n$ 以及 $P(x_1,x_2,\dots ,x_n)$，它们的信息熵可以由链式法则表达为：

$$\begin{array}{rl}H(X_1,X_2,\dots X_n)& =H(X_1)+H(X_2\mid X_1)+\cdots +H(X_n\mid X_{n-1}\dots ,X_1)\\ & =\sum _{i=1}^{n}H(X_i\mid X_1,\dots ,X_{i-1})\end{array}$$

3.3.3 相对熵（KL 散度）

  相对熵（Relative Entropy），也叫 KL 散度 (Kullback-Leibler Divergence)，具有非负的特性。用于衡量两个分布之间距离的指标，用 $P$ 分布近似 $Q$ 的分布，相对熵可以计算这个中间的损失，但是不对称（$P$ 对 $Q$ 和 $Q$ 对 $P$ 不相等），因此不能表示两个分布之间的距离，这种非对称性意味着选择 $D_{\mathrm{K}\mathrm{L}}(P\Vert Q)$ 还是 $D_{\mathrm{K}\mathrm{L}}(Q\Vert P)$ 影响很大。当 $P=Q$ 时， 相对熵（$\mathrm{K}\mathrm{L}$ 散度）$D_{\mathrm{K}\mathrm{L}}(P\Vert Q)$取得最小值 $0$。

  如果对于同一个随机变量 $x$ 有两个单独的概率分布 $P(x)$ 和 $Q(x)$，我们就可以使用 $\mathrm{K}\mathrm{L}$ 散度来衡量这两个分布的差异。$\mathrm{K}\mathrm{L}$ 散度越小，真实分布与近似分布之间的匹配就越好。

$$D_{\mathrm{K}\mathrm{L}}(P\Vert Q)={\mathbb{E}}_{\mathrm{x}\sim P}\left[\log \frac{P(x)}{Q(x)}\right]={\mathbb{E}}_{\mathrm{x}\sim P}[\log P(x)-\log Q(x)]$$

其中 $D_{\mathrm{S}K}(P\Vert Q)$ 的值域 $P,Q$ 分布的接近程度是呈正相关的。

我们将 $\mathrm{K}\mathrm{L}$ 散度公式变形得到：
$$\begin{array}{rl}{D}_{\mathrm{K}\mathrm{L}}(P\Vert Q)& ={\mathbb{E}}_{\mathrm{x}\sim P}[\log P(x)-\log Q(x)]\\ & ={\mathbb{E}}_{\mathrm{x}\sim P}[\log P(x)]-{\mathbb{E}}_{\mathrm{x}\sim P}[\log Q(x)]\\ & =-H(P)-{\mathbb{E}}_{\mathbf{x}\sim P}[\log Q(x)]\\ & =H_Q(P)-H_P(P)\end{array}$$

为了保证 $\mathrm{K}\mathrm{L}$ 散度的连续性，约定：

$$0\log \frac{0}{0}=0,0\log \frac{0}{Q}=0,P\log \frac{P}{0}=\infty$$
当 $P=Q$ 时,两者之间的相对熵 $D_{\mathrm{K}\mathrm{L}}(P\Vert Q)=0$

  $Eq.()$ 中的 $H_Q(P)$ 表示使用分布 $Q$ ，对分布 $P$ 进行编码所需的平均编码 $\mathrm{b}\mathrm{i}\mathrm{t}$ 数，$H_P(P)$ 表示使用分布 $P$ ，对分布 $P$ 编码所需的最小编码 $\mathrm{b}\mathrm{i}\mathrm{t}$ 数。因此相对熵的的意义可以理解为：$D_{\mathrm{K}\mathrm{L}}(P\Vert Q)$ 表示对于分布 $P$ ，使用 $Q$ 分布进行编码相较于使用真实分布 $P$ 进行编码（即最优编码）多出来的 $\mathrm{b}\mathrm{i}\mathrm{t}$ 数，也即是两个分布之间的差异。

  在机器学习中，$P$ 往往用来表示样本的真实分布，$Q$ 用来表示模型所预测的分布，那么 $\mathrm{K}\mathrm{L}$ 散度就可以计算两个分布的差异，也就是 损失函数 $\mathcal{L}$：
$$D_{\mathrm{K}\mathrm{L}}(P\Vert Q)={\mathbb{E}}_{\mathrm{x}\sim P}\left[\log \frac{P(x)}{Q(x)}\right]=\sum _{i=1}^{n}P(x_i)\log \frac{P(x_i)}{Q(x_i)}$$

离散：
$$D_{\mathrm{K}\mathrm{L}}(P||Q)=-\sum _{i}P(i)\ln \frac{Q(i)}{P(i)}=\sum _{i}P(i)\ln \frac{P(i)}{Q(i)}$$

连续：
$$D_{\mathrm{K}\mathrm{L}}(P||Q)={\int }_{-\infty }^{\infty }p(x)\ln \frac{p(x)}{q(x)}dx$$

我们可以利用不等式 $\log x\le x-1$ 即可证明 $\mathrm{K}\mathrm{L}$ 散度一定大于 $0$：

考虑连续的 $\mathrm{K}\mathrm{L}$ 散度，设有两个概率密度 $P(x),Q(x)$，假设 $Q(x)>0$，则有 $\mathrm{K}\mathrm{L}$ 散度：

$$\begin{array}{rlr}D(P\Vert Q)& =\int P(x)\log \frac{P(x)}{Q(x)}\text{dx}& \\ & =-\int P(x)\log \frac{Q(x)}{P(x)}\text{dx}& \\ & \ge -\int P(x)\left(\frac{Q(x)}{P(x)}-1\right)\text{dx}& \\ & =-\int Q(x)-P(x)\text{dx}& \text{【概率密度函数积分值等于 1】}\\ & =0& \end{array}$$

得证 $\square$

更多 $\mathrm{K}\mathrm{L}$ 散度图像上的直观解释详见：初学机器学习：直观解读KL散度的数学概念

3.3.4 交叉熵

  我们在上一节 3.3.3 相对熵（KL 散度） 中得到 $\mathrm{K}\mathrm{L}$ 散度的公式：

$$D_{\mathrm{K}\mathrm{L}}(P\Vert Q)=H_Q(P)-H_P(P)$$

其中$H_Q(P)$ 表示使用分布 $Q$ ，对分布 $P$ 进行编码所需的平均编码 $\mathrm{b}\mathrm{i}\mathrm{t}$ 数，$H_P(P)$ 表示使用分布 $P$ ，对分布 $P$ 编码所需的最小编码 $\mathrm{b}\mathrm{i}\mathrm{t}$ 数。

           \,\,\,\,\,\,\,\,\,\, 因此我们定义 交叉熵（Cross Entropy） $CEH(P,Q)=H_Q(P)$，即：

$$\begin{array}{rl}CEH(P,Q)& =H_Q(P)\\ & =-{\mathbb{E}}_{x\sim P}\log Q\left(x\right)\\ & =-\sum _{i=0}^{n}P(x_i){\log }_{b}Q(x_i)\end{array}$$

表示使用分布 $Q$ ，对分布 $P$ 进行编码所需的平均编码 $\mathrm{b}\mathrm{i}\mathrm{t}$ 数。

  至此，我们定义的 $P$ 与 $Q$ 之间的交叉熵 $CEH$ 就等于 $P$ 的熵 $H(P)$ 与 $P,Q$ 的 $\mathrm{K}\mathrm{L}$ 散度 $D_{\mathrm{K}\mathrm{L}}(P\Vert Q)$ 之和：

$$CEH(P,Q)=H(P)+D_{\mathrm{K}\mathrm{L}}(P\Vert Q)$$

           \,\,\,\,\,\,\,\,\,\, 由于$\mathrm{K}\mathrm{L}$ 散度是不对称的，显然交叉熵也是不对称的：
$$\begin{array}{rl}CEH(P,Q)& \ne CEH(Q,P)\\ D_{KL}(P\mid Q)& \ne D_{KL}(Q\mid P)\end{array}$$

  在机器学习任务中，我们希望使用分布 $Q$ 去拟合分布 $P$ ，需要评估标签与预测值之间的差距，可以直接使用 $\mathrm{K}\mathrm{L}$ 散度，即 $D_{\mathrm{K}\mathrm{L}}(\mathbf{y}\Vert \hat{\mathbf{y}})$。而由于分布 $P$ 不变，即 $H(P)$ 保持不变，交叉熵 $CEH(P,Q)$ 的变化就可以直接反映出相对熵 $D_{\mathrm{K}\mathrm{L}}(P\Vert Q)$ 的变化。由于相对熵 $D_{\mathrm{K}\mathrm{L}}(P\Vert Q)$ 中包含定值 $H(P)$ ，是一个不可优化的常数，且实验表明交叉熵在训练时相较于相对熵更加 健壮（robust），因此我们一般直接用交叉熵作为损失函数来评估模型，而不是使用相对熵 $\mathrm{K}\mathrm{L}$ 散度。

  交叉熵可以很好地衡量 $2$ 个分布之间的差别，特别地，当分类问题中 $y$ 的编码分布 $P$ 采用 one-hot 编码时：$H(\mathbf{y})=0$，此时
$$CEH(\mathbf{y},\mathbf{o})=H(\mathbf{y})+D_{KL}(\mathbf{y}|\mathbf{o})=D_{KL}(\mathbf{y}|\mathbf{o})$$
退化到真实标签分布 $\mathbf{y}$ 与输出概率分布 $\mathbf{o}$ 之间的 $\mathrm{K}\mathrm{L}$ 散度上。

根据 $\mathrm{K}\mathrm{L}$ 散度的定义，我们推导分类问题中交叉熵的计算表达式：

$$\begin{array}{rl}CEH(\mathbf{y},\mathbf{o})& =D_{KL}(\mathbf{y}|\mathbf{o})=\sum _j{y}_j\log \left(\frac{y_j}{o_j}\right)\\ & =1\times \log \frac{1}{o_i}+\sum _{j\ne i}0\times \log \left(\frac{0}{o_j}\right)\\ & =-\log o_i\end{array}$$

其中 $i$ 为 one-hot 编码中为 $1$ 的索引号，也是当前输入的真实类别。可以看到，损失函数 $\mathcal{L}$ 只与真实类别 $i$ 上的概率 ${\mathbf{o}}_i$ 有关，对应概率 ${\mathbf{o}}_i$ 越大，$H(\mathbf{y},\mathbf{o})$ 越小，当对应概率为 $1$ 时，交叉熵 $H(\mathbf{y},\mathbf{o})$ 取得最小值 $0$ ，此时网络输出 $\mathbf{o}$ 与真实标签 $\mathbf{y}$ 完全一致，神经网络取得最优状态。最小化交叉熵的过程也是最大化正确类别的预测概率的过程。

3.3.5 JS 散度

           \,\,\,\,\,\,\,\,\,\, JS 散度 (Jensen-Shannon Divergence)，度量了两个概率分布的相似度，是基于 $\mathrm{K}\mathrm{L}$ 散度的变体，解决了 $\mathrm{K}\mathrm{L}$ 散度非对称的问题。

           \,\,\,\,\,\,\,\,\,\, 一般地，JS 散度是对称的，其取值是 $0$ 到 $1$ 之间。定义如下：
$$JS(P_1\Vert P_2)=\frac{1}{2}KL(P_1\Vert \frac{P_1+P_2}{2})+\frac{1}{2}KL(P_2\Vert \frac{P_1+P_2}{2})$$

           \,\,\,\,\,\,\,\,\,\, 因而JS散度拥有对称性，并且在形式上更为平滑，更适合作为最后最大似然的函数，这点在生成对抗网络（GAN）的损失函数取得了不错的成绩。

KL 散度和 JS 散度的问题

           \,\,\,\,\,\,\,\,\,\, 如果两个分布 $P,Q$ 离得很远，完全没有重叠的时候，那么 KL 散度值是没有意义的，而 JS 散度值是一个常数。这在学习算法中是比较致命的，这就意味着这一点的梯度为 $0$，出现了梯度消失现象，导致训练失败。

           \,\,\,\,\,\,\,\,\,\, 这里通过一个简单的分布实例来解释 JS 散度的缺陷。考虑完全不重叠 （$\theta \ne 0$）的两个分布 $p$ 和 $q$ ，其中分布 $p$ 为：

$$\begin{array}{l}\forall (x,y)\in p,x=0,y\sim \mathrm{U}(0,1)\end{array}$$

分布 $q$ 为：

$$\forall (x,y)\in q,x=\theta ,y\sim \mathrm{U}(0,1)$$

其中 $\theta \in \mathbb{R}$，当 $\theta =0$ 时，分布 $p$ 和 $q$ 重叠，两者相等；当 $\theta \ne 0$ 时，分布 $p$ 和 $q$ 不重叠。分布 $p$ 和 $q$ 的示意图如图 3.12 所示。

图 3.12 分布 p 和 q 的示意图

  

我们来分析上述分布 $p$ 和 $q$ 之间的 JS 散度随 $\theta$ 的变化情况。根据 KL 散度与 JS 散度的定义，计算 $\theta =0$ 时的 JS 散度 $D_{\mathrm{J}\mathrm{S}}(p\Vert q)$：

$$\begin{gathered} D_{KL}(p\Vert q)=\sum _{x=0,y\sim \mathrm{U}(0,1)}1\cdot \log \frac{1}{0}=+\infty \\ {D}_{KL}(q\Vert p)=\sum _{x=\theta ,y\sim \mathrm{U}(0,1)}1\cdot \log \frac{1}{0}=+\infty \\ {D}_{JS}(p\Vert q)=\frac{1}{2}\left(\sum _{x=0,y\sim U(0,1)}1\cdot \log \frac{1}{1/2}+\sum _{x=0,y\sim U(0,1)}1\cdot \log \frac{1}{1/2}\right)=\log 2 \end{gathered}$$

当 $\theta =0$ 时，两个分布完全重叠，此时的 JS 散度和 KL 散度都取得最小值，即 $D_{KL}(p\Vert q)=D_{KL}(q\Vert p)=D_{JS}(p\Vert q)=0$。

至此我们可以得到 $D_{\mathrm{J}\mathrm{S}}(q\Vert p)$ 随 $\theta$ 的变化趋势：

$$D_{\mathrm{J}\mathrm{S}}(p\Vert q)=\{\begin{array}{cc}\log 2& \theta \ne 0\\ 0& \theta =0\end{array}$$

也就是说，当两个分布完全不重叠时，无论分布之间的距离远近，JS 散度为恒定值 $\log 2$，此时 JS 散度将无法产生有效的梯度信息；当两个分布出现重叠时，JS 散度才会平滑变动，产生有效梯度信息；当完全重合后，JS 散度取得最小值 $0$。如图 3.13 中所示，红色的曲线分割两个正态分布，由于两个分布没有重叠，生成样本位置处的梯度值始终为 $0$，无法更新生成网络的参数，从而出现网络训练困难的现象。

图 3.13 JS 散度出现梯度弥散现象 [21]

  

因此，JS 散度在分布 $p$ 和 $q$不重叠时是无法平滑地衡量分布之间的距离，从而导致此位置上无法产生有效梯度信息，出现 GAN 训练不稳定的情况。要解决此问题，需要使用一种更好的分布距离衡量标准，使得它即使在分布 $p$ 和 $q$ 不重叠时，也能平滑反映分布之间的真实距离变化。

3.3.6 Wasserstein 距离

Wasserstein距离 ，度量两个概率分布之间的距离。WGAN 论文发现了 JS 散度导致 GAN 训练不稳定的问题，并引入了一种新的分布距离度量方法：Wasserstein 距离，它表示了从一个分布变换到另一个分布的最小代价，定义如下：
$$W(P_1,P_2)=\underset{\gamma \sim \prod (P_1,P_2)}{\inf }{\mathbb{E}}_{(x,y)\sim \gamma }[\Vert x-y\Vert ]$$

其中 $\prod (P_1,P_2)$ 是 $P_1$ 和 $P_2$ 分布组合起来的所有可能的联合分布的集合。对于每一个可能的联合分布 $\gamma$，可以从中采样 $(x,y)\sim \gamma$ 得到一个样本 $x$ 和 $y$，并计算出这对样本的距离 $\Vert x-y\Vert$，所以可以计算该联合分布 $\gamma$ 下，样本对距离的期望值 $E_{(x,y)\sim \gamma }[||x-y||]$。在所有可能的联合分布中能够对这个期望值取到的下确界 ${\inf }_{\gamma \sim \Pi (P_1,P_2)}{E}_{(x,y)\sim \gamma }[||x-y||]$ 就是 Wasserstein 距离。

直观上可以把 $E_{(x,y)\sim \gamma }[||x-y||]$ 理解为在 $\gamma$ 这个路径规划下把土堆 $P_1$ 挪到土堆 $P_2$ 所需要的消耗。而 Wasserstein 距离就是在最优路径规划下的最小消耗。所以 Wesserstein 距离又称推土机距离（Earth-Mover Distance，简称 EM 距离）。

继续考虑图 3.12 中的示例，我们可以得出分布 $p$ 和 $q$ 之间的 EM 距离的表达式：

$$W(p,q)=|\theta |$$

绘制出 JS 散度和 EM 距离的曲线，如图 3.14 所示，可以看到，JS 散度在 $\theta =0$ 处不连续，其他位置导数均为 $0$，而 EM 距离总能够产生有效的导数信息，因此 EM 距离相对于JS 散度更适合指导 GAN 网络的训练。

图 3.14 JS 散度和 EM 距离随 变换曲线

  

Wessertein距离相比 KL 散度和 JS 散度的优势在于：即使两个分布的支撑集没有重叠或者重叠非常少，仍然能反映两个分布的远近。而 JS 散度在此情况下是常量，KL 散度可能无意义。

更多关于Wasserstein 距离的讲解详见： GAN的Loss的比较研究（3）——Wasserstein Loss理解（1） 以及 令人拍案叫绝的Wasserstein GAN

参考资料

[1] 《2021春机器学习课程》李宏毅
https://speech.ee.ntu.edu.tw/~hylee/ml/2021-spring.html

[2]《TensorFlow深度学习》（龙龙老师）
https://github.com/dragen1860/Deep-Learning-with-TensorFlow-book

[3] Coursera吴恩达《神经网络与深度学习》
https://www.deeplearning.ai/

[4] 《动手学深度学习》第二版
https://zh-v2.d2l.ai/

[5] 《深度学习》（花书）
https://github.com/exacity/deeplearningbook-chinese

[6] relu函数为分段线性函数，为什么会增加非线性元素
https://www.cnblogs.com/lzida9223/p/10972783.html

[7] 【机器学习】神经网络-激活函数-面面观(Activation Function)
https://blog.csdn.net/cyh_24/article/details/50593400

[8] Logistic Regression (LR) 详解与更多相关的面试问题
https://blog.csdn.net/songbinxu/article/details/79633790

[9] 【机器学习】逻辑回归（非常详细）
https://zhuanlan.zhihu.com/p/74874291

[10] softmax回归(Softmax Regression)
https://blog.csdn.net/u012328159/article/details/72155874

[11] 逻辑回归算法原理及用于解决多分类问题
https://blog.csdn.net/AIHUBEI/article/details/104301492

[12] 逻辑回归（Logistic Regression）（二）
https://zhuanlan.zhihu.com/p/28415991

[13] 数学基础_4——信息论
https://blog.csdn.net/CesareBorgia/article/details/120817481

[14] 信息论（1）——熵、互信息、相对熵
https://zhuanlan.zhihu.com/p/36192699

[15] 一文读懂机器学习分类算法（附图文详解）
https://zhuanlan.zhihu.com/p/82114104

[16] An in-depth guide to supervised machine learning classification
https://builtin.com/data-science/supervised-machine-learning-classification

[17] 信息熵是什么？- 知乎
https://www.zhihu.com/question/22178202/answer/223017546

[18] 熵 (信息论) - 维基百科
https://zh.wikipedia.org/wiki/%E7%86%B5_(%E4%BF%A1%E6%81%AF%E8%AE%BA)

[19] 信息熵到底是什么
https://blog.csdn.net/saltriver/article/details/53056816

[20] Visual Information Theory

https://colah.github.io/posts/2015-09-Visual-Information/#fnref1

[21] M. Arjovsky, S. Chintala 和 L. Bottou, “Wasserstein Generative Adversarial Networks,” Proceedings of the 34th International Conference on Machine Learning, International Convention Centre, Sydney, Australia, 2017.

---

谢谢！

  

转载请注明出处：https://fanfansann.blog.csdn.net/
版权声明：本文为 CSDN 博主 「繁凡さん」（博客），知乎答主 「繁凡」（专栏），Github 「fanfansann」（全部源码），微信公众号 「繁凡的小岛来信」（文章 P D F 版））原创整理的文章，遵循CC 4.0 BY-NC-SA 版权协议，转载请附上原文出处链接及本声明。