1 时间复杂度对比#
本节我们只关注堆排序的时间复杂度.
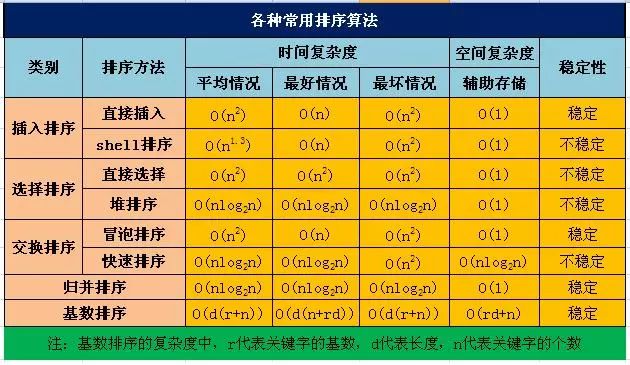
首先, 从上图我们可以看到,堆排序是不稳定的.
排序算法的稳定性: 对于一组数,如果相同元素的相对位置在排序前后保持一致,则该算法是稳定的,否则是不稳定的.
其次, 堆排序的时间复杂度都是O(nlogn), 空间复杂度是O(1).
2 算法#
2.1 堆的定义##
通常我们所说的堆都是指二叉堆.
二叉堆是一个完全二叉树或近似完全二叉树.
同时,二叉堆具有两个特性:
- 父节点的值总是大于或等于(or 小于或等于)任何一个子节点的值.
- 每个节点的左子树和右子树都是一个二叉堆.
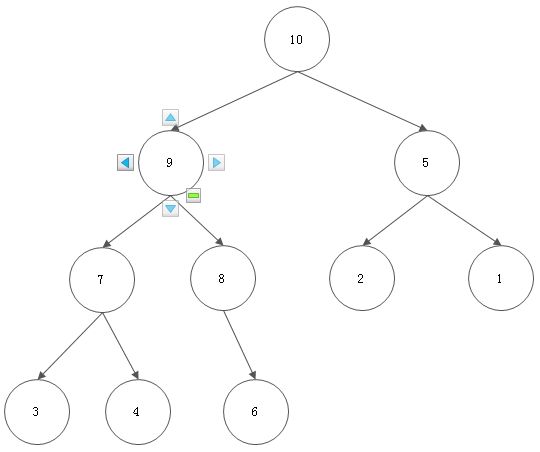
下面就是一个二叉堆的示例.
大根堆: 当父节点的值总是大于或等于任何一个子节点的值时,这个堆叫大根堆.
小根堆: 当父节点的值总是小于或等于任何一个子节点的值时,这个堆叫小根堆.
上图的示例就是一个大根堆.
2.2 堆的存储和节点访问##
堆一般使用数组存储,通过计算下标来访问父节点和子节点.
这样的特点也使得在使用堆排序的时候,没有额外的内存消耗去保存堆.
对于一个数组下标为i的节点,其父节点和左右子节点的下标计算方法分别为:
- 父节点下标 parentIndex(i) = i % 2 == 0 ? i / 2 -1 : i / 2;
- 左孩子节点下标 leftChildIndex(i) = i * 2 + 1;
- 右孩子节点下标 rightChildIndex(i) = i * 2 + 2;
2.3 建堆
建堆的过程:
从第一个非叶子节点(下标为(len - 2) / 2, 可以通过实例来找到下标的规律)开始到下标为0的节点, 逐个调整以当前节点为顶的子堆,市值满足大根堆或者小根堆的要求.
相关代码:
bool HeapSort::buildHeap(int* array, int len)
{
for (int index = indexOfLastNotLeafNode(len);
index >= 0;
--index)
{
adjust(array, len, index);
}
}
2.4 堆调整
堆调整是一个递归的过程, 顺序为从上往下:
先调整堆顶节点, 使之满足大根堆或者小根堆的要求. 例如, 如果是大根堆, 则当堆顶节点小于左孩子节点时, 交换两个节点, 再比较新的堆顶节点和右孩子节点的大小, 并做响应的调整.
相关代码:
void HeapSort::adjust(int* array, int len, int index)
{
if (index >= len)
{
return;
}
int left = leftChildIndex(index);
int right = rightChildIndex(index);
if (left < len && array[index] < array[left])
{
swap(array, index, left);
}
if (right < len && array[index] < array[right])
{
swap(array, index, right);
}
adjust(array, len, left);
adjust(array, len, right);
}
2.5 堆排序
堆排序就是使用上面的两个过程完成.
对于给定的一组数
- 首先建堆
- 取出堆顶元素,该堆顶元素为最大或者最小元素,将堆顶元素和堆中的最后一个叶子节点进行交换(节省空间),此时堆顶元素到达了最终的位置,下一次调整不需要考虑这些元素..
- 对剩下的堆进行调整.
- 重复步骤2和步骤3,直到堆中只剩下一个元素.
3 实现#
#include
#include "../common/array.h"
class HeapSort
{
public:
HeapSort() {};
void Run(int* array, int len);
private:
bool buildHeap(int* array, int len);
int indexOfLastNotLeafNode(int len);
void adjust(int* array, int len, int index);
inline int parentIndex(int index)
{
return index % 2 == 0 ? index / 2 - 1: index / 2;
}
inline int leftChildIndex(int index)
{
return index * 2 + 1;
}
inline int rightChildIndex(int index)
{
return index * 2 + 2;
}
inline void swap(int* array, int index1, int index2)
{
int temp = array[index1];
array[index1] = array[index2];
array[index2] = temp;
}
};
void HeapSort::adjust(int* array, int len, int index)
{
if (index >= len)
{
return;
}
int left = leftChildIndex(index);
int right = rightChildIndex(index);
if (left < len && array[index] < array[left])
{
swap(array, index, left);
}
if (right < len && array[index] < array[right])
{
swap(array, index, right);
}
adjust(array, len, left);
adjust(array, len, right);
}
int HeapSort::indexOfLastNotLeafNode(int len)
{
return (len - 2) / 2;
}
bool HeapSort::buildHeap(int* array, int len)
{
for (int index = indexOfLastNotLeafNode(len);
index >= 0;
--index)
{
adjust(array, len, index);
}
}
void HeapSort::Run(int* array, int len)
{
if (len <= 0)
{
return 0;
}
buildHeap(array, len);
for (int lastIndex = len - 1; lastIndex > 0; --lastIndex)
{
swap(array, 0, lastIndex);
adjust(array, lastIndex/*current length*/, 0/*heap top*/);
}
}
int main()
{
int array1[10] = {7,3,2,9,8,5,1,10,4,6};
int array2[1] = {7};
int array3[2] = {7, 3};
int array4[3] = {7, 3, 5};
HeapSort sort;
sort.Run(array1, 10);
sort.Run(array2, 1);
sort.Run(array3, 2);
sort.Run(array4, 3);
common::array::print(array1, 10);
common::array::print(array2, 1);
common::array::print(array3, 2);
common::array::print(array4, 3);
}