Python小白 Leetcode刷题历程 No.36-No.40 有效的数独、解数独、外观数列、组合总和、组合总和Ⅱ
写在前面:
作为一个计算机院的大学生,总觉得仅仅在学校粗略的学习计算机专业课是不够的,尤其是假期大量的空档期,作为一个小白,实习也莫得路子,又不想白白耗费时间。于是选择了Leetcode这个平台来刷题库。编程我只学过基础的C语言,现在在自学Python,所以用Python3.8刷题库。现在我Python掌握的还不是很熟练,算法什么的也还没学,就先不考虑算法上的优化了,单纯以解题为目的,复杂程度什么的以后有时间再优化。计划顺序五个题写一篇日志,希望其他初学编程的人起到一些帮助,写算是对自己学习历程的一个见证了吧。
有一起刷LeetCode的可以关注我一下,我会一直发LeetCode题库Python3解法的,也可以一起探讨。
觉得有用的话可以点赞关注下哦,谢谢大家!
········································································································································································
No.36.有效的数独
难度:中等
题目描述:
题解代码(Python3.8)
class Solution:
def isValidSudoku(self, board: List[List[str]]) -> bool:
set_box=set()
for i in range(9):
for j in range(9):
if board[i][j].isdigit():
row = 'row_'+str(i)+' ' + board[i][j]
col = 'col_'+str(j)+' ' + board[i][j]
small_square = 'row-col_'+str(i//3)+'-'+str(j//3)+' ' + board[i][j]
if row in set_box or col in set_box or small_square in set_box:
return False
set_box.update([row,col,small_square])
return True
或许有用的知识点:
set.add(key)可以在set中添加一个元素,set.remove(key)可以在set中删除一个元素。
如果想在set中一次性假如多个元素,可使用set.update([key1,key2,key3])。
解题思路:
在数独9宫格中,每个数字必定带有三个特性:行数、列数、小方块位置。对于一个i行j列的元素n,我们不妨定义它的特性为,row=row_i n , col=col_j n , small_square=row-col_(i//3)-(j)//3 n。对于每个数,我们将他的三个特性储存到一个set中。当新一个数字的三个特性都不在set中,我们便将其写入set;如果新一个数字有特性已经在set中了,不满足条件,返回False。
No.37.解数独
难度:困难
题目描述:
题解代码(Python3.8)
class Solution:
def solveSudoku(self, board: List[List[str]]) -> None:
row = [set(range(1,10)) for _ in range(9)] #行剩余可用数字
col = [set(range(1,10)) for _ in range(9)] #列剩余可用数字
block = [set(range(1,10)) for _ in range(9)] #块剩余可用数字
empty = [] #收集空白位置
for i in range(9):
for j in range(9):
if board[i][j] != '.':
val = int(board[i][j])
row[i].remove(val)
col[j].remove(val)
block[(i//3)*3+(j//3)].remove(val)
else:
empty.append((i,j))
def backtrack(iter_=0):
if iter_ == len(empty):
return True
i,j = empty[iter_]
block_index = (i//3)*3+(j//3)
for val in row[i] & col [j] & block[block_index]:
row[i].remove(val)
col[j].remove(val)
block[block_index].remove(val)
board[i][j] = str(val)
if backtrack(iter_+1):
return True
row[i].add(val)
col[j].add(val)
block[block_index].add(val)
return False
backtrack()
或许有用的知识点:
这道题需要使用回溯算法。
set( range(j) ) for _ in range(i),可以制作一个i行j列的set型二维数组,例如set( range(3)) for _ in range(4) = [ {0,1,2} , {0,1,2} , {0,1,2} , {0,1,2} ]。
要求列表A,B,C的公共元素,应使用 A & B & C ,(逻辑运算 and or not 只会返回运算的布尔值)。
解题思路:
先确定回溯函数,对比回溯函数模板,回溯出口为iter_长度与empty相等,回溯主体中在当发现子状态的有效解后进入下一状态,否则回溯到原来状态。
之后初始化状态,要有行剩余可用数字、列剩余可用数字、块剩余可用数字、空白方格位置。最后调用回溯函数即可。
No.38.外观数列
难度:简单
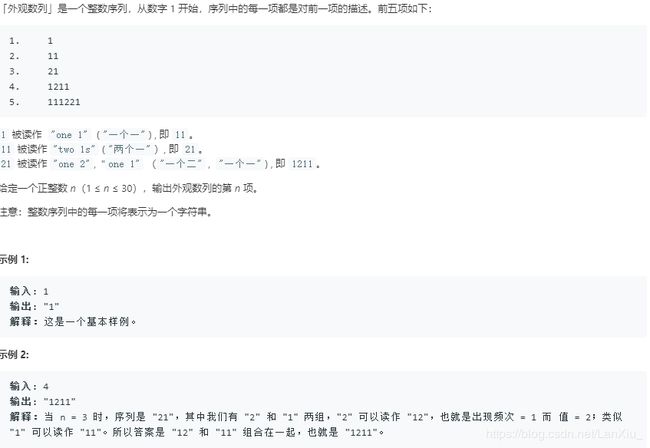
题目描述:
题解代码(Python3.8)
class Solution:
def countAndSay(self, n: int) -> str:
prev_person = '1'
for i in range(1,n):
next_person,num,count = '',prev_person[0],1
for j in range(1,len(prev_person)):
if prev_person[j] == num:
count +=1
else:
next_person += str(count)+num
num = prev_person[j]
count =1
next_person += str(count)+num
prev_person = next_person
return prev_person
解题思路:
这个题就是题比较难读懂,我翻译了一下,其实就是:
1.1
2.描述的是1,是一个1,也就是11
3.描述的是11,是两个1,也就是21
- 描述的是21,是一个2一个1,也就是12-11
- 描述的是1211, 是一个1,一个2,两个1,也就是11-12-21
- 描述的是111221,是三个1,两个2,一个1,也就是31-22-11
- 描述的是312211,是一个3一个1两个2两个1,也即是13-11-22-21
以此类推
所以对字符串进行一次遍历就好,将已生成的最后一个数称为‘上一个数’,再通过‘上一个数’推出‘下一个数’,然后把‘下一个数’的值赋给上一个数,继续遍历即可。
No.39.组合总和
难度:中等
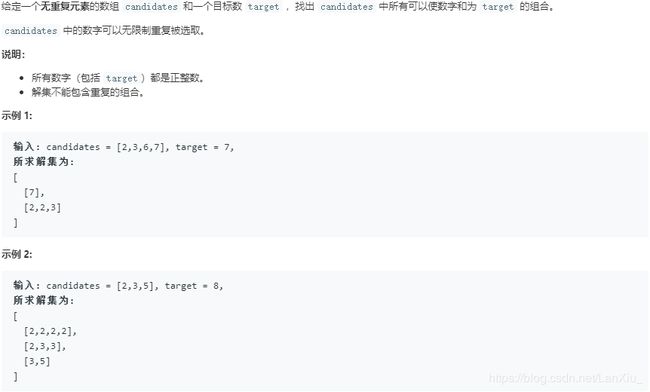
题目描述:
题解代码(Python3.8)
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
l=len(candidates)
if l==0:
return []
candidates.sort()
path=[]
res=[]
def backtrack(begin,path,target):
if target==0:
res.append(path[:])
for i in range(begin,l):
target_next=target-candidates[i] #剪枝操作
if target_next<0:
break
path.append(candidates[i])
backtrack(i,path,target_next)
path.pop()
backtrack(0,path,target)
return res
或许有用的知识点:
这道题要用到回溯算法。
a=p与a=p[:]的区别:a=p是把p的地址给a,p和a指向同一对象;而a=p[:]是创建一个内容与p全等的对象,命名为a,a指向p的副本,p和a指向不同对象。再回溯算法中,对可能被回溯的待保存元素,有时需要以a=p[:] 的方式储存。
解题思路:
定义回溯函数,在减的过程中,得到 0或者负数,就没有必要再走下去,所以这两种情况就分别表示成为叶子结点。此时递归结束,然后要发生回溯。注意,这道题中组合里的数字可以无限制重复被选取。而要想完成剪枝,前提是数组是有序的,因此我们需要对数组进行排序。注意,Python 中可变对象是引用传递,因此需要将当前 path 里的值拷贝出来,即a=p[:]。
No.40.组合总和Ⅱ
难度:中等
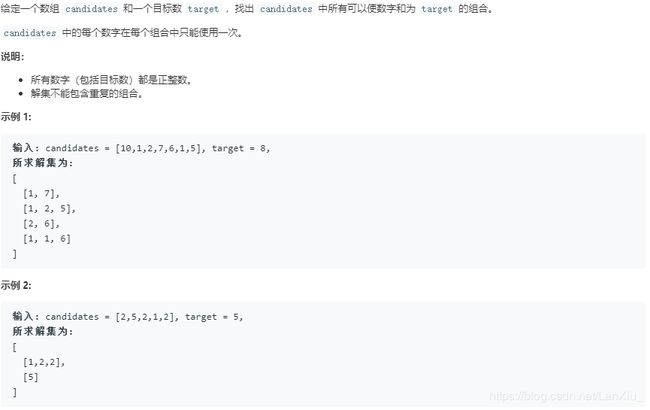
题目描述:
题解代码(Python3.8)
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
l=len(candidates)
if l==0:
return []
candidates.sort() #初始化
path=[]
res=[]
def backtrack(begin,path,target):
if target==0: #回溯出口
res.append(path[:])
for i in range(begin,l): #回溯主体
target_next=target-candidates[i] #剪枝操作
if target_next<0:
break
if i>begin and candidates[i-1]==candidates[i]:
continue
path.append(candidates[i])
backtrack(i+1,path,target_next)
path.pop() #状态返回
backtrack(0,path,target)
return res
或许有用的知识点:
这道题要用到回溯算法。
a=p与a=p[:]的区别:a=p是把p的地址给a,p和a指向同一对象;而a=p[:]是创建一个内容与p全等的对象,命名为a,a指向p的副本,p和a指向不同对象。再回溯算法中,对可能被回溯的待保存元素,有时需要以a=p[:] 的方式储存。
解题思路:
这道题跟‘39.组合总和’的思路类似,都是定义回溯函数,与其差别就是这道题组合中每个数只能用使用一次。在减的过程中,得到 0或者负数,就没有必要再走下去,所以这两种情况就分别表示成为叶子结点。此时递归结束,然后要发生回溯。要想完成剪枝,前提是数组是有序的,因此我们需要对数组进行排序。注意,Python 中可变对象是引用传递,因此需要将当前 path 里的值拷贝出来,即a=p[:]。