堆的定义:
n个元素序列{k1,k2,...,ki,...,kn},当且仅当满足下列关系时称之为堆:
(ki<= k2i,ki<= k2i+1) 或者 (ki>= k2i,ki>= k2i+1), (i = 1,2,3,4,...,n/2)
堆数据结构是一种数组对象,它可以被视为一种完全二叉树结构。它的特点是父节点的值大于(小于)两个子节点的值(分别称为大顶堆和小顶堆)。它常用于管理算法执行过程中的信息,应用场景包括堆排序,优先队列等
堆的操作:
http://blog.csdn.net/hrn1216/article/details/51465270
堆的建立:将给定的序列按层次遍历建立完全二叉树,然后从最后一个非终端结点开始自下向上逐步调整为堆。
堆的删除:堆中每次都只能删除堆顶元素。将最后一个数据的值赋给根结点,然后再从根结点开始进行一次从上向下的调整。调整时先在左右子结点中找最小的,如果父结点比这个最小的子结点还小说明不需要调整了,反之将父结点和它交换后再考虑后面的结点。相当于根结点数据的“下沉”过程。
堆的插入:将新元素放到序列的最后,从下向上逐步进行调整。
堆的排序:在输出堆顶的最小值之后,使得剩余n-1个元素的序列重建一个堆,则得到n个元素中的次小值。如此反复执行,便能得到一个有序序列,这个过程称之为堆排序。在用堆排序算法排序时,如果要进行增序排序,则需要采用“大根堆”,减序排列则要采用“小根堆”。
树的种类:
完美(Perfect)二叉树:一个深度为k(>=-1)且有2^(k+1) - 1个结点的二叉树
完全(Complete)二叉树:从根结点到倒数第二层满足完美二叉树,最后一层可以不完全填充,其叶子结点都靠左对齐。
完满(Full)二叉树:所有非叶子结点的度都是2。
二叉排序树(二叉查找树\二叉搜索树):1. 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;2. 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;3. 它的左、右子树也分别为二叉排序树。
平衡二叉树(AVL树):它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
哈夫曼树:它是 n 个带权叶子结点构成的所有二叉树中,带权路径长度 WPL 最小的二叉树。
二叉树的遍历:
前序遍历:1.访问根节点中序遍历、后序遍历 2.前序遍历左子树 3.前序遍历右子树
中序遍历:1.中序遍历左子树 2.访问根节点 3.中序遍历右子树
后序遍历:1.后序遍历左子树 2.后序遍历右子树 3.访问根节点
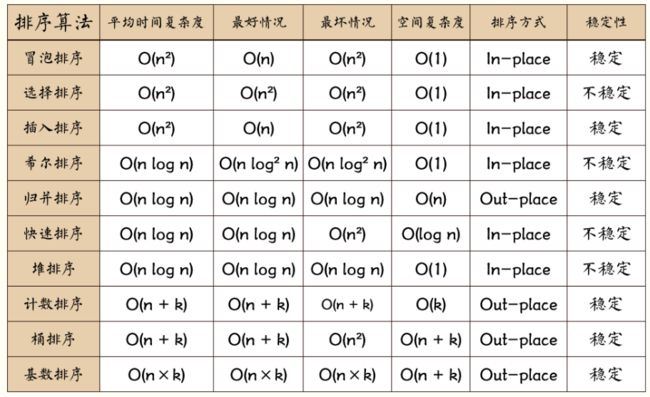
排序对比:
PS:
算法复杂度中的O(logN)底数是多少? http://blog.csdn.net/jdbc/article/details/42173751