【知识图谱论文】MINERVA:使用强化学习对知识库中的路径进行推理
Article
文献题目:Go for a Walk and Arrive at the Answer: Reasoning Over Paths in Knowledge Bases with Reinforcement Learning
文献时间:2018
发表期刊:ICIR
https://github.com/shehzaadzd/MINERVA
摘要
自动和手动构建的知识库 (KB) 通常是不完整的——通过综合现有信息可以从 KB 中推断出许多有效的事实。知识库补全的一种流行方法是通过对沿着连接一对实体的其他路径发现的信息进行组合推理来推断新关系。鉴于 KB 的巨大规模和路径的指数数量,以前的基于路径的模型只考虑了在给定两个实体的情况下预测缺失关系的问题,或者评估所提出的三元组的真实性。此外,这些方法传统上使用固定实体对之间的随机路径,或者最近学会在它们之间选择路径。我们提出了一种新算法 MINERVA,它解决了在关系已知但只有一个实体的情况下回答更困难和更实际的任务。由于随机游走在从起始节点开始组合多个目的地的环境中是不切实际的,因此我们提出了一种神经强化学习方法,该方法学习如何根据输入查询导航图以找到预测路径。根据经验,这种方法在几个数据集上获得了最先进的结果,显着优于以前的方法。自动和手动构建的知识库 (KB) 通常是不完整的——通过综合现有信息可以从 KB 中推断出许多有效的事实。知识库补全的一种流行方法是通过对沿着连接一对实体的其他路径发现的信息进行组合推理来推断新关系。鉴于 KB 的巨大规模和路径的指数数量,以前的基于路径的模型只考虑了在给定两个实体的情况下预测缺失关系的问题,或者评估所提出的三元组的真实性。此外,这些方法传统上使用固定实体对之间的随机路径,或者最近学会在它们之间选择路径。我们提出了一种新算法 MINERVA,它解决了在关系已知但只有一个实体的情况下回答更困难和更实际的任务。由于随机游走在从起始节点开始组合多个目的地的环境中是不切实际的,因此我们提出了一种神经强化学习方法,该方法学习如何根据输入查询导航图以找到预测路径。根据经验,这种方法在几个数据集上获得了最先进的结果,显着优于以前的方法。
1 引言
- 自动推理,即计算系统根据观察到的证据做出新推断的能力,一直是人工智能的长期目标。 我们对具有丰富多样语义的大型知识库 (KB) 上的自动推理感兴趣。 知识库是高度不完整的,通常可以从知识库中推断出不直接存储在知识库中的事实,这为自动推理创造了令人兴奋的机遇和挑战。 例如,考虑图 1 中的小知识图。我们可以从以下推理路径推断出 Colin Kaepernick 的(未观察到的事实)主场:Colin Kaepernick → PlaysInTeam → 49ers →TeamHomeStadium → Levi’s Stadium。 我们的目标是在 KB 中自动学习这种推理路径。 我们将学习问题构建为查询回答之一,也就是说,回答以下形式的问题 (Colin Kaepernick, PlaysInLeague, ?)。
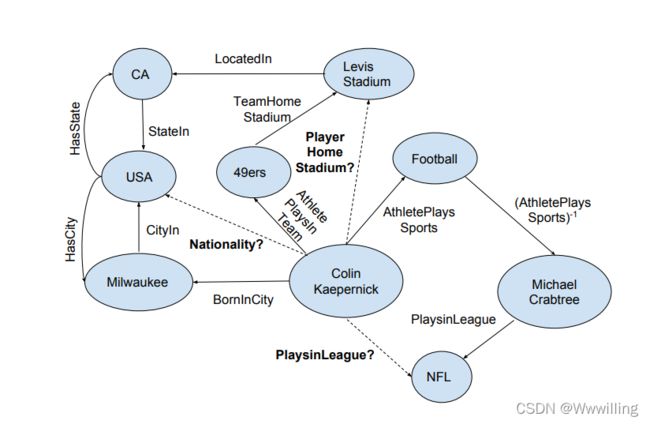
- 图 1:表示为知识图的知识库的一小部分。 观察到实心边缘,虚线边缘是查询的一部分。 请注意如何通过实体“Colin Kaepernick”和相应答案之间的“逻辑”路径遍历图形来回答每个查询(例如 Nationality、PlaysInLeague、Layer HomeStadium)
- 从早期开始,自动推理方法的重点一直是构建可以学习清晰的符号逻辑规则的系统符号表示也已与机器学习集成,特别是在统计关系学习中,但由于泛化性能差,这些方法在很大程度上已被被分布式向量表示所取代。使用张量分解或神经方法学习实体和关系的嵌入一直是一种流行的方法(Nickel 等人,2011;Bordes 等人,2013;Socher 等人,2013;除其他外),但这些方法无法捕获知识库路径表达的推理。神经多跳模型通过在向量空间中对 KB 路径进行操作,在一定程度上解决了上述问题。然而,这些模型将一组路径作为输入,这些路径是通过执行独立于查询关系的随机游走收集的。此外,诸如使用相同的一组最初收集的路径来回答不同的查询类型(例如,MarriedTo、Nationality、WorksIn 等)的模型。
- 本文提出了一种使用强化学习 (RL) 以输入问题为条件的有效搜索提供答案路径的图的方法,无需预先计算的路径。 给定一个庞大的知识图谱,我们学习一个策略,给定查询(实体,关系,?),从实体开始,并通过在每一步选择带标签的关系边来学习走到答案节点,条件是 查询关系和整个路径历史。 这将查询-回答任务表述为强化学习 (RL) 问题,其目标是采取最佳决策序列(关系边的选择)以最大化预期奖励(到达正确答案节点)。 我们将 RL 代理 MINERVA 称为“在实体网络中蜿蜒以达到相似答案”。
- 我们基于 RL 的配方具有许多理想的特性。 首先,MINERVA 具有采用可变长度路径的内置灵活性,这对于回答需要复杂推理链的更难的问题非常重要。 其次,MINERVA 不需要预训练,通过强化学习从头开始训练知识图谱; 不需要其他监督或微调,这代表了 RL 在 NLP 中的先前应用的显着进步。 第三,我们的基于路径的方法在计算上是有效的,因为通过在查询实体周围的一个小邻域中进行搜索,它避免了像之前的工作那样对 KB 中的所有实体进行排名。 最后,我们的智能体找到的推理路径自动形成其预测的可解释来源。
- 这篇论文的主要贡献是:(a)我们提出了代理 MINERVA,它通过在以输入查询为条件的知识图上行走来学习查询回答,当它到达答案节点时停止。代理使用强化学习进行训练,特别是策略梯度(第 2 节)。 (b) 我们在几个基准数据集上评估 MINERVA,并与在 KB 中进行逻辑规则学习的 Neural Theorem Provers (NTP) 和 Neural LP 进行比较。 © 我们还与 DeepPath 进行比较,后者使用强化学习来选择实体对之间的路径。主要区别在于,他们的 RL 代理的状态包括答案实体,因为它是为更简单的任务而设计的,即预测事实是否为真或不是。因此,他们的方法不能直接应用于我们更具挑战性的查询回答任务,其中第二个实体未知且必须推断。尽管如此,在他们的实验设置中进行比较时,MINERVA 在他们的基准 NELL-995 数据集上的表现优于 DeepPath。
2 任务与模型
- 我们在 KB 中正式定义了查询回答的任务。 令 E E E 表示实体集, R R R 表示二元关系集。 那么 KB 是存储为三元组 ( e 1 , r , e 2 ) (e_1,r, e_2) (e1,r,e2) 的事实集合,其中 e 1 , e 2 ∈ E e_1, e_2 ∈ E e1,e2∈E 和 r ∈ R r ∈ R r∈R。查询回答旨在回答形式为 ( e 1 , r , ? ) (e_1,r, ?) (e1,r,?) 的问题,例如Toronto, locatedIn, ?。 我们还想清楚地指出查询回答和事实预测任务之间的区别。 事实预测涉及预测事实是否真实,例如 (Toronto, locatedIn, Canada)? 这个任务比在查询回答中预测正确的实体作为答案更容易,因为后者需要在许多可能的实体中找到答案实体。
- 接下来,我们将描述如何将 KB 中的查询回答问题简化为有限范围的顺序决策问题,并使用强化学习来解决它。 我们首先将环境表示为从知识库(第 2.1 节)派生的知识图 G G G 上的确定性马尔可夫决策过程。 我们的 RL 代理得到了一个形式为 ( e 1 q , r q , ? ) (e_{1q},r_q,?) (e1q,rq,?) 的输入查询。 从知识图 G G G 中 e 1 q e_{1q} e1q 对应的顶点开始,agent 学习遍历环境/图来挖掘答案,并在确定答案时停止(第 2.2 节)。 代理使用策略梯度更具体地由 REINFORCE 使用控制变量进行训练(第 2.3 节)。 让我们从描述环境开始。
2.1 环境 - 状态、动作、转换和奖励
- 我们的环境是一个有限范围确定性和部分观察到的马尔可夫决策过程,它位于从 KB 派生的知识图谱上。 回想一下,KB 是存储为三元组 ( e 1 , r , e 2 ) (e_1,r,e_2) (e1,r,e2) 的事实集合,其中 e 1 , e 2 ∈ E e_1,e_2 ∈ E e1,e2∈E 和 r ∈ R r ∈ R r∈R。从 KB 可以构建知识图 G G G,其中实体 s , t s,t s,t 表示为节点,关系 r r r 表示为它们之间的标记边。 此外,按照之前的方法,我们添加每条边的逆关系,即对于边 ( e 1 , r , e 2 ) ∈ E (e_1,r, e_2) ∈ E (e1,r,e2)∈E,我们将边 ( e 2 , r − 1 , e 1 ) (e_2,r^{−1}, e_1) (e2,r−1,e1) 添加到图中。 在这个图上,我们现在将指定一个确定性的部分可观察马尔可夫决策过程,我们将在下面详细说明。
- 状态。 状态空间由具有实体集的所有可能的查询-答案笛卡尔积组成。 直观地说,我们想要一个状态来编码查询 ( e 1 q , r q ) (e_{1q},r_q) (e1q,rq)、答案 ( e 2 q ) (e_{2q}) (e2q) 和探索位置 e t e_t et(实体的当前节点)。 因此,总体而言,状态由 ( e t , e 1 q , r q , e 2 q ) (e_t, e_{1q},r_q, e_{2q}) (et,e1q,rq,e2q) 表示,并且状态空间由所有有效组合组成。
- 观察。 环境的完整状态是不可观察的,但只能观察到它当前的探索和查询位置,而不能观察到答案,即只观察到 ( e t , e 1 q , r q ) (e_t, e_{1q},r_q) (et,e1q,rq)。
- 行动。 来自状态 S = ( e t , e 1 q , r q , e 2 q ) S = (e_t , e_{1q},r_q, e_{2q}) S=(et,e1q,rq,e2q) 的一组可能动作 A S A_S AS 由 G G G 和 NO-OP 中的顶点 e t e_t et 的所有输出边组成。 基本上,这意味着每个状态的代理都可以选择它希望采用的输出边,同时了解边 r r r 和目标顶点 t t t 的标签,或者不采取任何行动并保持在当前顶点。
- 过渡。 通过仅将状态更新到代理通过其动作选择的边缘所指向的新顶点,环境确定性地演变。 查询和答案保持不变。
- 奖励。 如果当前位置是最后的正确答案,我们只有 +1 的最终奖励,否则为 0。 详细地说,如果 S T = ( e t , e 1 q , r q , e 2 q ) S_T = (e_t, e_{1q},r_q, e_{2q}) ST=(et,e1q,rq,e2q) 是最终状态,那么如果 e t = e 2 q e_t = e_{2q} et=e2q,我们将获得 +1 的奖励,否则为0。
2.2 策略网络
- 为了解决上述有限水平确定性部分可观察马尔可夫决策过程,我们旨在设计一个随机历史相关策略 π = ( d 1 , d 2 , . . . , d T − 1 ) π = (d_1,d_2,...,d_{T−1}) π=(d1,d2,...,dT−1),其中 d t : H t → P ( A S t ) d_t:H_t → P(A_{S_t}) dt:Ht→P(ASt) 和 历史 H t = ( H t − 1 , A t − 1 , O t ) H_t = (H_{t−1},A_{t−1},O_t) Ht=(Ht−1,At−1,Ot) 只是观察和采取的行动的序列。我们将自己限制在由长短期记忆网络 (LSTM) 表示的函数类中,用于学习随机历史相关策略 .
- 基于 LSTM 的代理将历史 H t H_t Ht 编码为连续向量 h t ∈ R 2 d h_t ∈ R^{2d} ht∈R2d。 我们还分别为二元关系和实体提供了嵌入矩阵 r ∈ R ∣ R ∣ × d r ∈ R^{|R|×d} r∈R∣R∣×d 和 e ∈ R ∣ E ∣ × d e ∈ R^{|E|×d} e∈R∣E∣×d。 H t = ( H t − 1 , A t − 1 , O t ) H_t = (H_{t−1},A_{t−1},O_t) Ht=(Ht−1,At−1,Ot) 的历史嵌入根据 LSTM 动态进行更新:
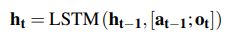
- 其中 a t − 1 ∈ R d a_{t−1} ∈ R^d at−1∈Rd 和 o t ∈ R d o_t ∈ R^d ot∈Rd 分别表示时间 t − 1 t-1 t−1 的动作/关系和时间 t t t 的观察/实体的向量表示, [ ; ] [;] [;] 表示向量连接。 为了阐明, a t − 1 = r A t − 1 a_{t-1} = r_{A_{t-1}} at−1=rAt−1 ,即嵌入对应于代理在时间 t − 1 t -1 t−1 和 o t = e e t o_t = e_{e_t} ot=eet 如果 O t = ( e t , e 1 q , r q ) O_t = (e_t , e_{1q},r_q) Ot=(et,e1q,rq) 时选择的边的标签的关系,即与代理顶点对应的实体的嵌入是在时间 t t t。
- 基于历史嵌入 h t h_t ht,策略网络根据查询关系做出从所有可用动作 ( A S t ) (A_{S_t}) (ASt) 中选择动作的决定。 回想一下,每个可能的动作都代表一条带有边关系标签 l l l 和目标顶点/实体 d d d 信息的输出边。 所以每个 A ∈ A S t A ∈ A_{S_t} A∈ASt 的嵌入是 [ r l ; e d ] [r_l; e_d] [rl;ed],并为所有出边堆叠嵌入,我们得到矩阵 A t A_t At。 将这些作为输入的网络被参数化为具有 ReLU 非线性的两层前馈网络,该网络接受当前历史表示 h t h_t ht 和查询关系 r q r_q rq 的嵌入,并输出可能的动作的概率分布,其中对离散动作进行采样。 换句话说,
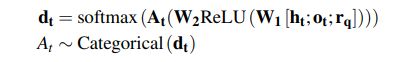
- 请注意, G G G 中的节点没有固定的顺序或从它们出来的边数。 矩阵 A t A_t At 的大小为 ∣ A S t ∣ × 2 d |A_{S_t}| ×2d ∣ASt∣×2d,因此决策概率 d t d_t dt 位于大小 ∣ A S t ∣ |A_{S_t}| ∣ASt∣ 的单纯形上。 此外,上述过程对于按要求呈现边缘的顺序是不变的,并且属于被设计为排列不变的神经网络的范围。 最后,总结一下,LSTM 的参数、权重 W 1 W_1 W1、 W 2 W_2 W2、相应的偏差(为简洁起见,上面没有显示)和嵌入矩阵构成了策略网络的参数 θ θ θ。
2.3 训练
- 对于上述策略网络 ( π θ ) (π_θ) (πθ),我们希望找到最大化预期奖励的参数 θ θ θ:
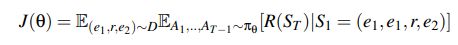
- 我们假设存在一个真正的潜在分布 ( e 1 , r , e 2 ) ∼ D (e_1,r, e_2) ∼ D (e1,r,e2)∼D。 为了解决这个优化问题,我们使用 REINFORCE 如下:
- 第一个期望被训练数据集的经验平均值取代。
- 对于第二个期望,我们通过为每个训练示例运行多个 rollout 来进行近似。 推出的数量是固定的,对于我们所有的实验,我们将此数字设置为 20。
- 为了减少方差,一种常见的策略是使用加法控制变量基线。 我们使用累积折扣奖励的移动平均值作为基线。 我们将此移动平均线的权重调整为超参数。 请注意,在我们的实验中,我们发现学习基线的表现相似,但由于其简单性,我们最终决定将累积折扣奖励作为基线。
- 实验细节 我们选择关系和嵌入维度大小为200。动作嵌入是通过连接实体和关系嵌入形成的。 我们使用维度大小为 400 的 3 层 LSTM。MLP 的隐藏层大小(权重 W 1 W_1 W1 和 W 2 W_2 W2)设置为 400。我们使用带有 REINFORCE 中默认参数的 Adam 进行更新。
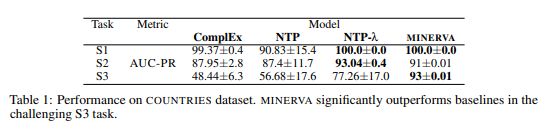
- COUNTRIES、KINSHIP、UMLS 我们首先在 COUNTRIES 数据集上测试我们的模型,该数据集明确设计用于测试模型学习逻辑规则的能力。 它包含国家、地区和次区域作为实体。 该数据集有 3 个任务(表 1 中的 S1-3),每个任务都需要增加长度和难度的推理步骤。 我们报告了 COUNTRIES 数据集的精确召回曲线 (AUC-PR) 下区域的性能。 我们还在 UMLS 和 KINSHIP 数据集上将 MINERVA 与 NeuralLP 进行了比较。
- 我们的实验设置和分数直接与表 1 相当,并在表 1 中报告。表 3 报告了 UMLS 和 KINSHIP 的结果,其中我们大大优于 NeuralLP。

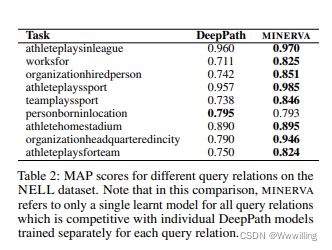
- NELL-995 我们还将 MINERVA 与 DEEPPATH 进行了比较。 为了公平比较,我们只对答案实体和它们发布的数据集中的否定示例进行排名。 但与他们不同的是,我们训练了一个模型来学习所有查询关系。 如果我们的模型无法找到正确的实体或负实体之一,则查询将获得负无穷大的分数。 如表 2 所示,我们在大多数情况下都优于它们,并且在其余查询关系中实现了可比的性能。
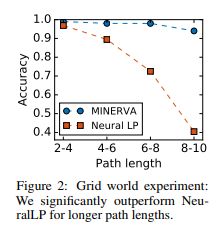
- GRID WORLD PATH FINDING 以前的工作指出,回答 KB 中的查询所需的推理链通常不会太长(限制为 3 或 4 跳)。 为了测试我们的模型是否可以学习长推理路径,我们在合成网格世界数据集上测试我们的模型,该数据集由任务从随机单元格(起始实体)开始导航到特定单元格(答案实体)并遵循一组 方向(查询关系)(例如北,西南)。 图 2 显示了不同路径长度的精度。 与 NEURALLP 相比,MINERVA 对于需要更长路径长度且性能几乎没有下降的查询更加健壮。
相关工作
- 使用张量分解或神经方法学习实体和关系的向量表示一直是使用知识库进行推理的流行方法。 但是,这些方法无法捕获更复杂的推理模式,例如通过遵循 KB 中的推理路径找到的那些。 多跳链路预测方法解决了上述问题,但它们操作的推理路径是通过执行独立于查询关系类型的随机游走来收集的。 Lao et al(2011) 根据路径必须在训练集中的目标实体之一结束并且在最大长度内的限制,进一步从采样路径集中过滤路径。 这些约束使它们依赖于查询,但它们本质上是启发式的。 我们的方法消除了预先计算路径的任何必要性,并学习有效地搜索以输入查询关系为条件的图。
- 归纳逻辑编程(ILP)旨在从示例和背景知识中学习通用谓词规则。 ILP 中的早期工作(例如 FOIL、PROGOL)要么基于规则,要么需要在 KB 中通常难以找到的反例(通过设计,KB 存储真实事实)。 统计关系学习方法和概率逻辑结合了机器学习和逻辑,但是这些方法对符号而不是向量进行操作,因此不具备基于嵌入的方法的泛化特性。
- 神经定理证明器 (NTP) 和神经 LP 是学习逻辑规则的两种最新方法,可以通过基于梯度的学习进行端到端训练。 NTP 由 Prolog 的反向链接推理方法构建。它对向量而不是符号进行操作,从而为每个证明路径提供成功分数。然而,由于可以在任何两个向量之间计算分数,因此在反向链接的替换步骤中,由于这种软匹配,计算图变得非常大。对于易处理性,它依赖于启发式方法,例如仅保留前 K 得分证明路径,但它失去了计算精确梯度的任何保证。此外,NTP 的功效尚未在大 KB 上显示出来。神经 LP 引入了使用 TensorLog 中定义的算子的微分规则学习系统,并具有基于 LSTM 的控制器和可微分的内存组件,并且通过注意力计算规则分数。尽管可微内存允许端到端地训练网络,但它需要访问整个内存,这在计算上可能是昂贵的。可以对内存进行硬选择的 RL 方法在计算上具有吸引力。 MINERVA 使用类似的硬选择关系边在图上行走。更重要的是,MINERVA 在各自的基准数据集上优于这两种方法。
- DeepPath 使用基于 RL 的方法来查找 KB 中的路径。然而,他们的 MDP 的状态需要提前知道目标实体,因此他们的寻路策略依赖于知道答案实体。 MINERVA 不需要目标实体的任何知识,而是学习在所有实体中找到答案实体。 DeepPath 还将其收集的路径提供给路径排名算法,而 MINERVA 是一个经过训练可以进行查询回答的完整系统。 DeepPath 还为其实体和关系使用固定的预训练嵌入。最后,在他们在 NELL 数据集上的实验设置中比较 MINERVA 和 DeepPath 时,我们匹配它们的性能或优于它们。 MINERVA 也类似于学习搜索结构化预测的方法。这些方法基于模仿参考策略(oracle),在每一步都做出接近最优的决策。在我们的问题设置中,尚不清楚什么是好的参考策略。例如,两个实体之间的最短路径预言是不好的,因为提供答案的路径应该取决于查询关系。
结论
- 作为这项正在进行的工作的一部分,我们探索了一种在大型知识库上进行自动推理的新方法,其中我们使用知识库的知识图表示并训练代理以根据输入查询走到答案节点。 我们在多个基准知识库完成任务上取得了最先进的结果,并且我们还表明我们的模型是稳健的并且可以学习长推理链。 此外,它不需要预训练或初始监督。 未来的研究方向包括应用更复杂的 RL 技术以及直接处理文本查询和文档。