机器学习基础学习-sklearn中的SVM

前言

理论部分参考支持向量机SVM（理论部分）
写代码之前，我们要把数据做标准化处理，因为SVM寻找的是使margin最大的中间的那根线，而我们衡量margin的方式是数据点之间的距离，这里涉及到距离，如果我们的数据点在不同的维度上，量纲不同，那我们对数据的估计是有问题的。
举个例子，下图有四个样本点，两个属于红色类别，两个属于蓝色类别。

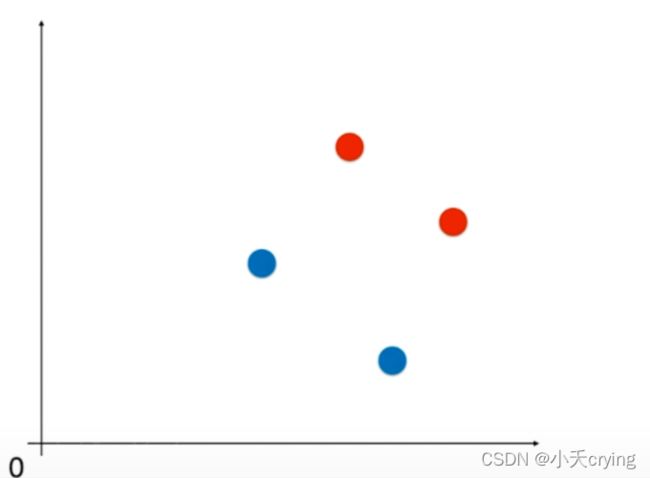
如果数据在这两个维度上数据尺度相差过大，例如横轴上范围在（0,1）,纵轴的范围是（0,10000）

此时使用SVM，得到的决策边界如下图所示，此时标记的两个点是我们的支撑向量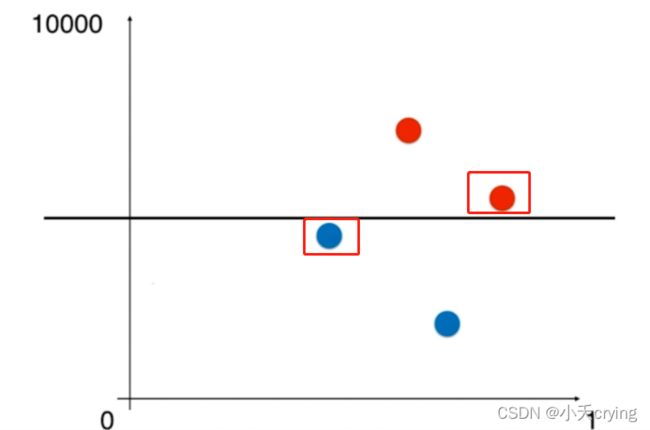
此时这两个点离我们决策边界的距离是最大的，但是视觉上他们的距离很短，因为纵轴的范围是（0,10000），实际上视觉上很短的距离也会代表很大的数

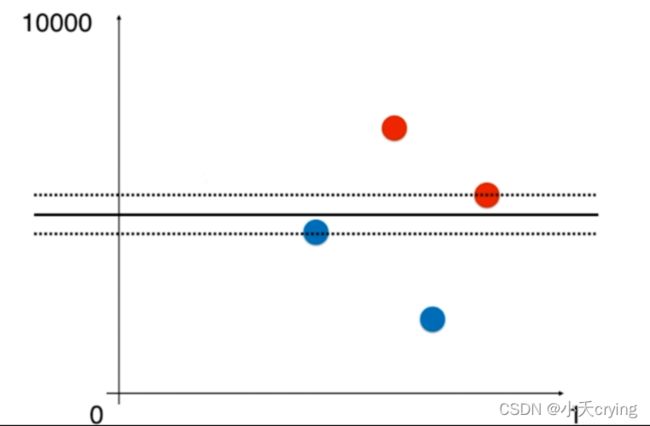
改变尺度
接下来如果我们的尺度发生变化，如果纵轴的范围也是（0,1），那么很显然决策边界如下图所示

在这种情况下，上面的四个点可能都是我们的支撑向量，那么margin对应的虚线则是

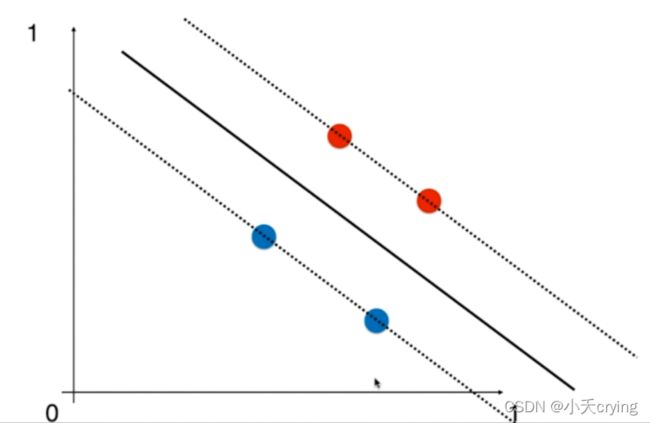
所以对于SVM算法来说，如果我们的特征在不同维度上数据尺度不同的话，将会非常严重的影响SVM算法得到的决策边界，为了避免这种情况的出现，我们将对所有的数据进行标准化处理

1、sklearn中的SVM

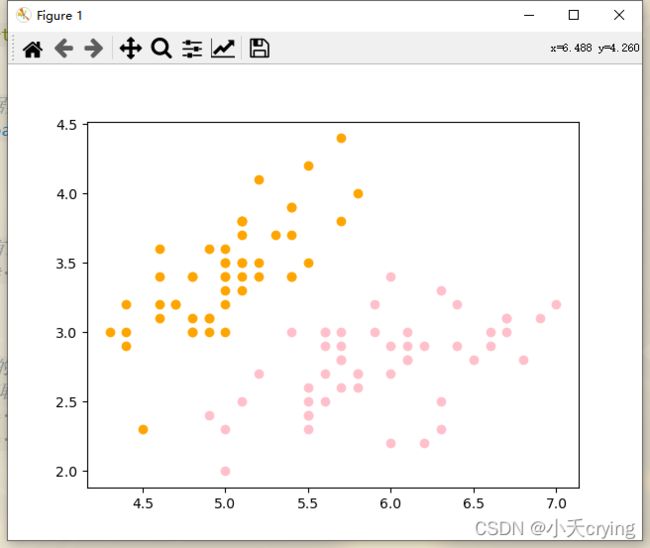
（1）采用鸢尾花数据集生成样本
这里我们实现二分类，所以我们只取鸢尾花分类当中的前两类，另外方便数据可视化，我们只取两个特征

'''
  生成样本
'''
import numpy as np
import matplotlib.pyplot as plt

from sklearn import datasets


# 这里先用鸢尾花数据集（150行4列：150个样本，4个特征值）
iris = datasets.load_iris()

X = iris.data
y = iris.target

# 这里鸢尾花数据集有三种分类，我们先把数据集做成只有两种分类（二分类）
X = X[y < 2, :2] # 取前两个特征方便可视化
y = y[y < 2]


# 绘制y=0、y=1相应的x的两个特征在二维平面的坐标,[y == 行范围, 列范围]
# X[y == 0, 1]：获取y==0的行，然后获取这些行的第二个元素
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()

（2）数据标准化

'''
  数据标准化
'''
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
# 这里只是为了数据可直观化，省去了训练集训练与测试的过程
standardScaler.fit(X)
X_standardScaler = standardScaler.transform(X)

（3）调用SVM算法并绘制决策边界

# 使用支持向量机的方法进行分类（线性SVM）
from sklearn.svm import LinearSVC
'''
  调用SVM（线性SVM）
  C:超参数（取值越大越偏向硬间隔，取值越小容错空间越大）
'''
svc = LinearSVC(C=1e9)
svc.fit(X_standardScaler, y)

# 绘制决策边界
plot_decision_boundary(svc, axis=[-3, 3, -3, 3])
# 绘制样本
plt.scatter(X_standardScaler[y == 0, 0], X_standardScaler[y == 0, 1], color = "orange")
plt.scatter(X_standardScaler[y == 1, 0], X_standardScaler[y == 1, 1], color = "pink")
plt.show()

这里附上绘制决策边界的方法plot_decision_boundary

'''
  绘制决策边界
  params-model:训练好的model
  params-axis:绘制区域坐标轴范围（0,1,2,3对应x轴和y轴的范围）
'''
def plot_decision_boundary(model, axis):
  # meshgrid:生成网格点坐标矩阵
  x0, x1 = np.meshgrid(
    # 通过linspace把x轴分成无数点
    # axis[1] - axis[0]是x的左边界减去x的右边界
    # axis[3] - axis[2]：y的最大值减去y的最小值
        
    # arr.shape    # (a,b)
    # arr.reshape(m,-1) #改变维度为m行、d列 （-1表示列数自动计算，d= a*b /m）
    # arr.reshape(-1,m) #改变维度为d行、m列 （-1表示行数自动计算，d= a*b /m ）
    np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
    np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
  )
  print('x0', x0)
  # print('x1', x1)
  # np.r_是按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等，相加后列数不变。
  # np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等，相加后行数不变。
  # .ravel():将多维数组转换为一维数组
  X_new = np.c_[x0.ravel(), x1.ravel()]
  y_predict = model.predict(X_new)
  
  # 这里不能zz = y_predict.reshape(x0.shape)，会报错'list' object has no attribute 'reshape'
  # 要通过np.array转换一下
  zz = np.array(y_predict).reshape(x0.shape)

  from matplotlib.colors import ListedColormap
  # ListedColormap允许用户使用十六进制颜色码来定义自己所需的颜色库，并作为plt.scatter()中的cmap参数出现：
  custom_cmap = ListedColormap(['#F5FFFA', '#FFF59D', '#90CAF9'])
  # coutourf([X, Y,] Z,[levels], **kwargs),contourf画的是登高线之间的区域
  # Z是和X,Y相同维数的数组。
  plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

这里C设置的是1e9，设置的非常大，所以本质上相当于一个Hard Margin SVM

（4）减小超参数C

'''
  重新实例化，减小超参数C
'''
svc2 = LinearSVC(C=0.01)
svc2.fit(X_standardScaler, y)

# 绘制决策边界
plot_decision_boundary(svc2, axis=[-3, 3, -3, 3])
# 绘制样本
plt.scatter(X_standardScaler[y == 0, 0], X_standardScaler[y == 0, 1], color = "orange")
plt.scatter(X_standardScaler[y == 1, 0], X_standardScaler[y == 1, 1], color = "pink")
plt.show()

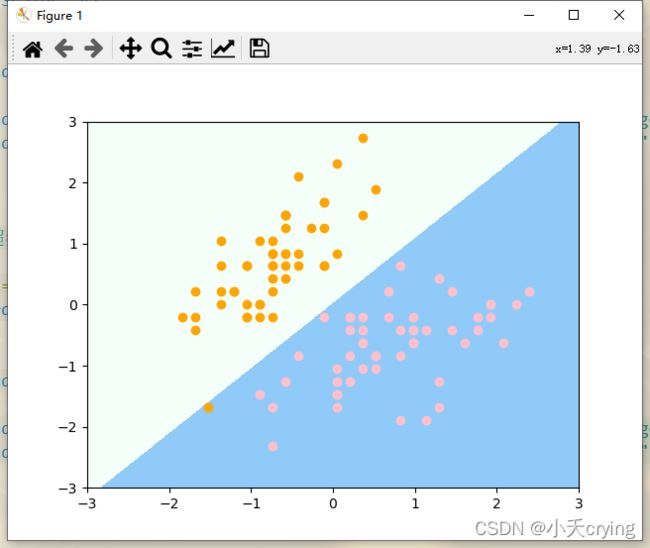
直观的看，改变C的大小，决策边界是不一样的，然后仔细观察第二次划分的决策边界，有一个橙色的点被错分到了错误的分类。这就是把C的值变小的结果，回顾之前说的，这里的C越大表示容错空间越小，而C越小表示容错空间越大，那么我们这里C取值很小的话，我们的SVM就会犯一个错误。

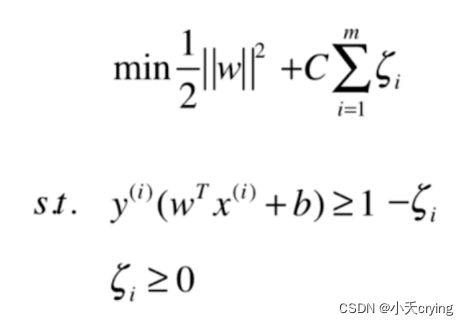
（5）绘制支撑向量所在的直线
首先训练之后我们可以看到决策边界的系数值

print(svc.coef_, 'svc系数值') # svc的系数值

对于现在的两个特征，每个特征对应了一个系数。
另外这个系数是个二维数组，因为sklearn封装的svm算法直接可以处理多分类问题，如果有多个类别，那么算法就会有多条直线分割特征平面，所以这里是二维数组（但我们这里是二分类问题，所以多维数组只有一项，在第一个元素中）

另外我们还可以看看截距这个属性

print(svc.intercept_, 'svc截距') # svc的系数值

对应一个一维向量，一根直线对应一个截距

有了以上的参数，我们就可以绘制margin对应的上下两根线。

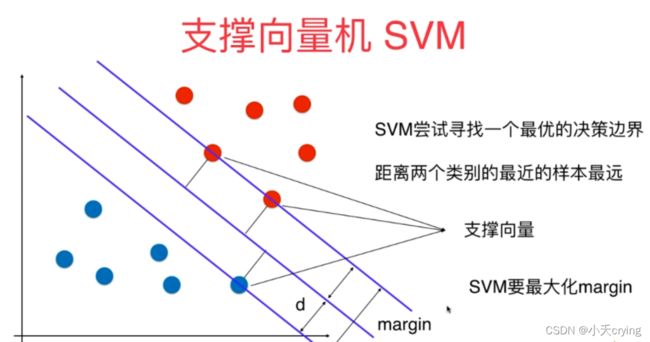
首先我们要新增一个基于改造绘制决策边界的函数用于绘制决策边界旁的两根线
增加的核心代码如下

  w = model.coef_[0] # coef_是二维数组
  b = model.intercept_[0]
  # 此时的决策边界应该是w0*x0+w1*x1+b=0
  # 上下的两根直线方程分别为w0*x0+w1*x1+b=1， w0*x0+w1*x1+b=-1
  # 为了方便可视化，以x1为纵轴，x0为横轴改写上面的直线方程
  # 决策边界：x1 = -w0/w1 * x0 - b/w1
  # 上下两根线：x1 = -w0/w1 * x0 - b/w1 + 1/w1；x1 = -w0/w1 * x0 - b/w1 - 1/w1
  plot_x = np.linspace(axis[0], axis[1], 200)
  # 接下来求对应x相应对上下两根线的y值
  up_y = -w[0]/w[1] * plot_x - b/w[1] + 1/w[1]
  down_y = -w[0]/w[1] * plot_x - b/w[1] - 1/w[1]
  # up_y、down_y有可能超过了axis规定的y轴的范围，需要对数据进行过滤
  up_index = (up_y >= axis[2]) & (up_y <= axis[3]) # 对应布尔数组
  down_index = (down_y >= axis[2]) & (down_y <= axis[3])
  # 绘制
  plt.plot(plot_x[up_index], up_y[up_index], color='red')
  plt.plot(plot_x[down_index], down_y[down_index], color='red')

总体函数代码

'''
  绘制svc决策边界根据margin计算的两根线
  params-model:训练好的model
  params-axis:绘制区域坐标轴范围（0,1,2,3对应x轴和y轴的范围）
'''
def plot_svc_decision_boundary(model, axis):
  # meshgrid:生成网格点坐标矩阵
  x0, x1 = np.meshgrid(
    # 通过linspace把x轴分成无数点
    # axis[1] - axis[0]是x的左边界减去x的右边界
    # axis[3] - axis[2]：y的最大值减去y的最小值
        
    # arr.shape    # (a,b)
    # arr.reshape(m,-1) #改变维度为m行、d列 （-1表示列数自动计算，d= a*b /m）
    # arr.reshape(-1,m) #改变维度为d行、m列 （-1表示行数自动计算，d= a*b /m ）
    np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
    np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
  )
  print('x0', x0)
  # print('x1', x1)
  # np.r_是按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等，相加后列数不变。
  # np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等，相加后行数不变。
  # .ravel():将多维数组转换为一维数组
  X_new = np.c_[x0.ravel(), x1.ravel()]
  y_predict = model.predict(X_new)
  
  # 这里不能zz = y_predict.reshape(x0.shape)，会报错'list' object has no attribute 'reshape'
  # 要通过np.array转换一下
  zz = np.array(y_predict).reshape(x0.shape)

  from matplotlib.colors import ListedColormap
  # ListedColormap允许用户使用十六进制颜色码来定义自己所需的颜色库，并作为plt.scatter()中的cmap参数出现：
  custom_cmap = ListedColormap(['#F5FFFA', '#FFF59D', '#90CAF9'])
  # coutourf([X, Y,] Z,[levels], **kwargs),contourf画的是登高线之间的区域
  # Z是和X,Y相同维数的数组。
  plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

  w = model.coef_[0] # coef_是二维数组
  b = model.intercept_[0]
  # 此时的决策边界应该是w0*x0+w1*x1+b=0
  # 上下的两根直线方程分别为w0*x0+w1*x1+b=1， w0*x0+w1*x1+b=-1
  # 为了方便可视化，以x1为纵轴，x0为横轴改写上面的直线方程
  # 决策边界：x1 = -w0/w1 * x0 - b/w1
  # 上下两根线：x1 = -w0/w1 * x0 - b/w1 + 1/w1；x1 = -w0/w1 * x0 - b/w1 - 1/w1
  plot_x = np.linspace(axis[0], axis[1], 200)
  # 接下来求对应x相应对上下两根线的y值
  up_y = -w[0]/w[1] * plot_x - b/w[1] + 1/w[1]
  down_y = -w[0]/w[1] * plot_x - b/w[1] - 1/w[1]
  # up_y、down_y有可能超过了axis规定的y轴的范围，需要对数据进行过滤
  up_index = (up_y >= axis[2]) & (up_y <= axis[3]) # 对应布尔数组
  down_index = (down_y >= axis[2]) & (down_y <= axis[3])
  # 绘制
  plt.plot(plot_x[up_index], up_y[up_index], color='red')
  plt.plot(plot_x[down_index], down_y[down_index], color='red')

进行绘制

# 绘制决策边界以及两根直线
plot_svc_decision_boundary(svc, axis=[-3, 3, -3, 3])
# 绘制样本
plt.scatter(X_standardScaler[y == 0, 0], X_standardScaler[y == 0, 1], color = "orange")
plt.scatter(X_standardScaler[y == 1, 0], X_standardScaler[y == 1, 1], color = "pink")
plt.show()

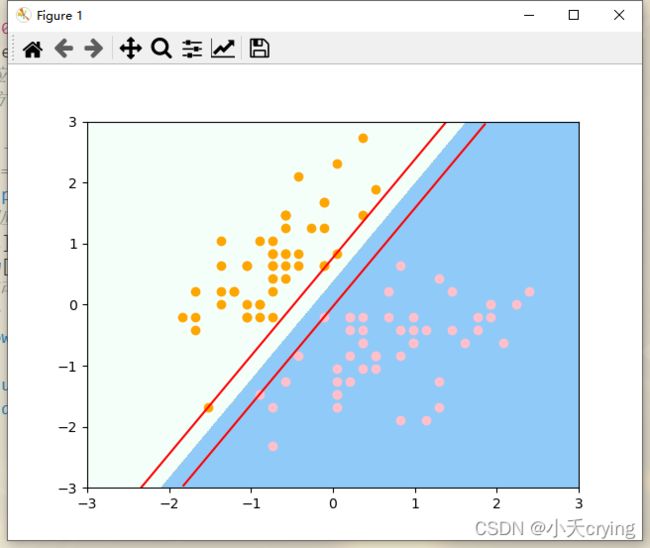
从这个图上我们可以看到，对于上半部分，有三个橙色的点落在了直线上；对于下半部分，有两个粉色的点落在了直线上，它们就是对应支撑向量。

（6）总结：
我们训练的这个svc模型相当于是Hard Margin SVM，所以在margin对应的两根直线中间是没有任何的数据点的，我们训练出的这个模型就是既保证正确的把数据集分成了两类，与此同时按照SVM的思想，让两类中离决策边界最近的点到决策边界的距离越远。

（7）后记
对比如果把超参数给的很小的情况，我们绘制决策边界和对应的两根直线

# svc2绘制决策边界以及两根直线
plot_svc_decision_boundary(svc2, axis=[-3, 3, -3, 3])
# 绘制样本
plt.scatter(X_standardScaler[y == 0, 0], X_standardScaler[y == 0, 1], color = "orange")
plt.scatter(X_standardScaler[y == 1, 0], X_standardScaler[y == 1, 1], color = "pink")
plt.show()

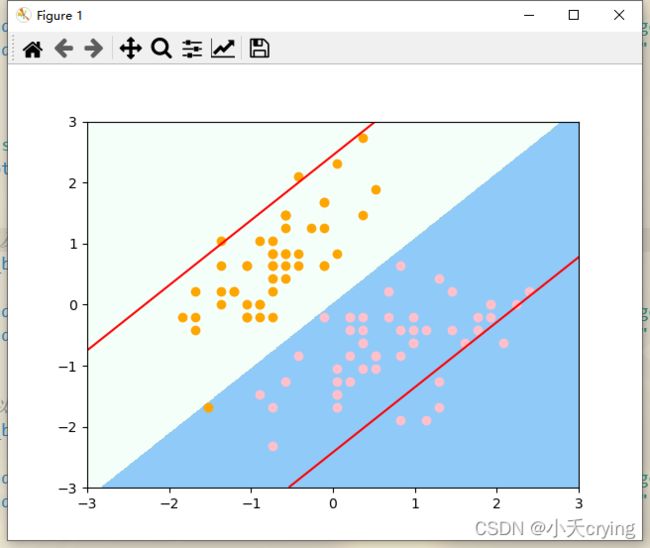
由于我们把C给的非常小，导致我们可以接受的容错空间很大，所以在margin对应的两根直线内有很多数据点。

以上所有部分没有通过svm进行预测，只是可视化的看到了svm算法对数据进行分类的样子。

基于以上实验，我们区分了训练集与测试集进行实验，用60%的数据用来实验，40%的数据用来测试，超参数选取1e9，属于hard margin SVM。并进行了精确度的测量

'''
  Hard Margin SVM
'''

import numpy as np
import matplotlib.pyplot as plt

from sklearn import datasets
from sklearn.preprocessing import StandardScaler

# 使用支持向量机的方法进行分类（线性SVM）
from sklearn.svm import LinearSVC

from sklearn.model_selection import train_test_split

'''
  绘制决策边界
  params-model:训练好的model
  params-axis:绘制区域坐标轴范围（0,1,2,3对应x轴和y轴的范围）
'''
def plot_decision_boundary(model, axis):
  # meshgrid:生成网格点坐标矩阵
  x0, x1 = np.meshgrid(
    # 通过linspace把x轴分成无数点
    # axis[1] - axis[0]是x的左边界减去x的右边界
    # axis[3] - axis[2]：y的最大值减去y的最小值
        
    # arr.shape    # (a,b)
    # arr.reshape(m,-1) #改变维度为m行、d列 （-1表示列数自动计算，d= a*b /m）
    # arr.reshape(-1,m) #改变维度为d行、m列 （-1表示行数自动计算，d= a*b /m ）
    np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
    np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
  )
  # print('x0', x0)
  # print('x1', x1)
  # np.r_是按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等，相加后列数不变。
  # np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等，相加后行数不变。
  # .ravel():将多维数组转换为一维数组
  X_new = np.c_[x0.ravel(), x1.ravel()]
  y_predict = model.predict(X_new)
  
  # 这里不能zz = y_predict.reshape(x0.shape)，会报错'list' object has no attribute 'reshape'
  # 要通过np.array转换一下
  zz = np.array(y_predict).reshape(x0.shape)

  from matplotlib.colors import ListedColormap
  # ListedColormap允许用户使用十六进制颜色码来定义自己所需的颜色库，并作为plt.scatter()中的cmap参数出现：
  custom_cmap = ListedColormap(['#F5FFFA', '#FFF59D', '#90CAF9'])
  # coutourf([X, Y,] Z,[levels], **kwargs),contourf画的是登高线之间的区域
  # Z是和X,Y相同维数的数组。
  plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)


'''
  绘制svc决策边界根据margin计算的两根线
  params-model:训练好的model
  params-axis:绘制区域坐标轴范围（0,1,2,3对应x轴和y轴的范围）
'''
def plot_svc_decision_boundary(model, axis):
  # meshgrid:生成网格点坐标矩阵
  x0, x1 = np.meshgrid(
    # 通过linspace把x轴分成无数点
    # axis[1] - axis[0]是x的左边界减去x的右边界
    # axis[3] - axis[2]：y的最大值减去y的最小值
        
    # arr.shape    # (a,b)
    # arr.reshape(m,-1) #改变维度为m行、d列 （-1表示列数自动计算，d= a*b /m）
    # arr.reshape(-1,m) #改变维度为d行、m列 （-1表示行数自动计算，d= a*b /m ）
    np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
    np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
  )
  # print('x0', x0)
  # print('x1', x1)
  # np.r_是按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等，相加后列数不变。
  # np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等，相加后行数不变。
  # .ravel():将多维数组转换为一维数组
  X_new = np.c_[x0.ravel(), x1.ravel()]
  y_predict = model.predict(X_new)
  
  # 这里不能zz = y_predict.reshape(x0.shape)，会报错'list' object has no attribute 'reshape'
  # 要通过np.array转换一下
  zz = np.array(y_predict).reshape(x0.shape)

  from matplotlib.colors import ListedColormap
  # ListedColormap允许用户使用十六进制颜色码来定义自己所需的颜色库，并作为plt.scatter()中的cmap参数出现：
  custom_cmap = ListedColormap(['#F5FFFA', '#FFF59D', '#90CAF9'])
  # coutourf([X, Y,] Z,[levels], **kwargs),contourf画的是登高线之间的区域
  # Z是和X,Y相同维数的数组。
  plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

  w = model.coef_[0] # coef_是二维数组
  b = model.intercept_[0]
  # 此时的决策边界应该是w0*x0+w1*x1+b=0
  # 上下的两根直线方程分别为w0*x0+w1*x1+b=1， w0*x0+w1*x1+b=-1
  # 为了方便可视化，以x1为纵轴，x0为横轴改写上面的直线方程
  # 决策边界：x1 = -w0/w1 * x0 - b/w1
  # 上下两根线：x1 = -w0/w1 * x0 - b/w1 + 1/w1；x1 = -w0/w1 * x0 - b/w1 - 1/w1
  plot_x = np.linspace(axis[0], axis[1], 200)
  # 接下来求对应x相应对上下两根线的y值
  up_y = -w[0]/w[1] * plot_x - b/w[1] + 1/w[1]
  down_y = -w[0]/w[1] * plot_x - b/w[1] - 1/w[1]
  # up_y、down_y有可能超过了axis规定的y轴的范围，需要对数据进行过滤
  up_index = (up_y >= axis[2]) & (up_y <= axis[3]) # 对应布尔数组
  down_index = (down_y >= axis[2]) & (down_y <= axis[3])
  # 绘制
  plt.plot(plot_x[up_index], up_y[up_index], color='red')
  plt.plot(plot_x[down_index], down_y[down_index], color='red')



'''
  生成样本
'''

# 这里先用鸢尾花数据集（150行4列：150个样本，4个特征值）
iris = datasets.load_iris()

X = iris.data
y = iris.target

# 这里鸢尾花数据集有三种分类，我们先把数据集做成只有两种分类（二分类）
X = X[y < 2, :2] # 取前两个特征方便可视化
y = y[y < 2]

# 绘制y=0、y=1相应的x的两个特征在二维平面的坐标,[y == 行范围, 列范围]
# X[y == 0, 1]：获取y==0的行，然后获取这些行的第二个元素
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4)

'''
  数据标准化
'''
standardScaler = StandardScaler()
# 这里只是为了数据可直观化（方便看清svm的分类以及软间隔C取值不同的结果）
standardScaler.fit(X_train)
X_standardScaler = standardScaler.transform(X_train)
X_testStandardScaler = standardScaler.transform(X_test)

'''
  调用SVM（线性SVM）
  C:超参数（取值越大越偏向硬间隔，取值越小容错空间越大）
'''
svc = LinearSVC(C=1e9)
svc.fit(X_standardScaler, y_train)

print('精确度', svc.score(X_testStandardScaler, y_test))

# 绘制决策边界
plot_decision_boundary(svc, axis=[-3, 3, -3, 3])
# 绘制决策边界以及两根直线
plot_svc_decision_boundary(svc, axis=[-3, 3, -3, 3])
# 绘制样本

plt.scatter(X_standardScaler[y_train == 0, 0], X_standardScaler[y_train == 0, 1], color = "orange")
plt.scatter(X_standardScaler[y_train == 1, 0], X_standardScaler[y_train == 1, 1], color = "pink")
plt.show()

2、SVM中使用多项式特征

处理非线性的数据，最典型的思路就是使用多项式的方式来扩充原本的数据，制造新的多项式特征。
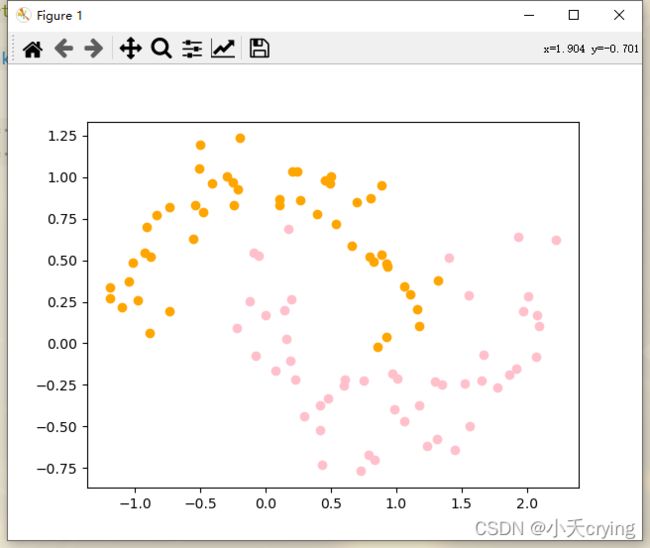
这里我们不使用真实的数据集，我们采用datasets的功能自动生成非线性的数据（make_moons）

（1）生成样本

'''
  SVM中使用多项式特征
'''

import numpy as np
import matplotlib.pyplot as plt

from sklearn import datasets

X, y = datasets.make_moons()
print(X.shape, 'X.shape')
print(y.shape, 'y.shape')

我们看一下生成的数据集

这里是一个100*2的矩阵，也就是100个样本，每个样本有两个特征，这是make_moons的默认参数，如果想生成高于100个样本或者多于2个特征的话，可以在make_moons中添加参数即可。

这里的y就是包含100个元素的向量，就是X中100个样本的分类结果。
接下来绘制样本

plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()

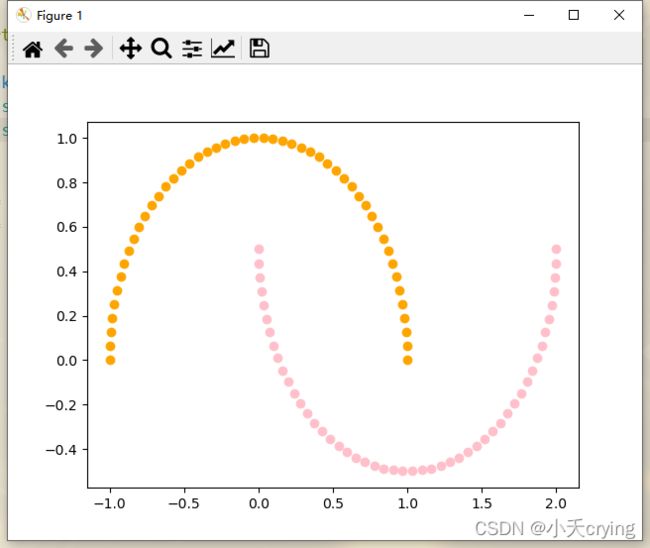
但是这个数据集分布太规则了，我们希望数据集还是存在部分扰动，我们在make_moons传入新的参数，添加噪音（在生成规则图形的基础上让标准差增大），这是随机的噪音，所以有随机化的影响，所以我们加上一个随机种子

X, y = datasets.make_moons(noise=0.15, random_state=666)

'''
  SVM中使用多项式特征
'''

import numpy as np
import matplotlib.pyplot as plt

from sklearn import datasets

X, y = datasets.make_moons(noise=0.15, random_state=666)
print(X.shape, 'X.shape')
print(y.shape, 'y.shape')

# 绘制样本
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()

（2）使用多项式特征的SVM
1）引入所需要的

from sklearn.preprocessing import PolynomialFeatures, StandardScaler # 引入多项式类、标准化
# 使用支持向量机的方法进行分类（线性SVM）
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline # 引入Pipeline顺序执行相关过程

2）我们构造一个pipeline，让我们需要的步骤顺序执行

'''
  svm中使用多项式特征
  degree: 阶数
'''
def PolynomialSVC(degree, C = 1.0):
  # 使用pipeline创建管道，送给实例化对象的数据会沿着管道的三步依次进行
  return Pipeline([ # Pipeline传入的是列表，列表中传入管道中每一步对应的类(这个类以元组的形式进行传送)
    ("poly", PolynomialFeatures(degree=degree)), # 第一步：求多项式特征，相当于poly = PolynomialFeatures(degree=2)
    ("std_scaler", StandardScaler()), # 第二步：数值的均一化
    ("linearSVC", LinearSVC(C = C)) # 第三步：进行线性回归操作
  ])

3）引入绘制决策边界的函数

'''
  绘制决策边界
  params-model:训练好的model
  params-axis:绘制区域坐标轴范围（0,1,2,3对应x轴和y轴的范围）
'''
def plot_decision_boundary(model, axis):
  # meshgrid:生成网格点坐标矩阵
  x0, x1 = np.meshgrid(
    # 通过linspace把x轴分成无数点
    # axis[1] - axis[0]是x的左边界减去x的右边界
    # axis[3] - axis[2]：y的最大值减去y的最小值
        
    # arr.shape    # (a,b)
    # arr.reshape(m,-1) #改变维度为m行、d列 （-1表示列数自动计算，d= a*b /m）
    # arr.reshape(-1,m) #改变维度为d行、m列 （-1表示行数自动计算，d= a*b /m ）
    np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
    np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
  )
  print('x0', x0)
  # print('x1', x1)
  # np.r_是按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等，相加后列数不变。
  # np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等，相加后行数不变。
  # .ravel():将多维数组转换为一维数组
  X_new = np.c_[x0.ravel(), x1.ravel()]
  y_predict = model.predict(X_new)
  
  # 这里不能zz = y_predict.reshape(x0.shape)，会报错'list' object has no attribute 'reshape'
  # 要通过np.array转换一下
  zz = np.array(y_predict).reshape(x0.shape)

  from matplotlib.colors import ListedColormap
  # ListedColormap允许用户使用十六进制颜色码来定义自己所需的颜色库，并作为plt.scatter()中的cmap参数出现：
  custom_cmap = ListedColormap(['#F5FFFA', '#FFF59D', '#90CAF9'])
  # coutourf([X, Y,] Z,[levels], **kwargs),contourf画的是登高线之间的区域
  # Z是和X,Y相同维数的数组。
  plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

4）训练，绘制决策边界

poly_svc = PolynomialSVC(degree=3)
poly_svc.fit(X, y) # 这里也是不区分训练集和测试集，所以所有数据都用来训练
# 绘制决策边界
plot_decision_boundary(poly_svc, axis=[-1.5, 2.5, -1.0, 1.5])
# 绘制样本
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()

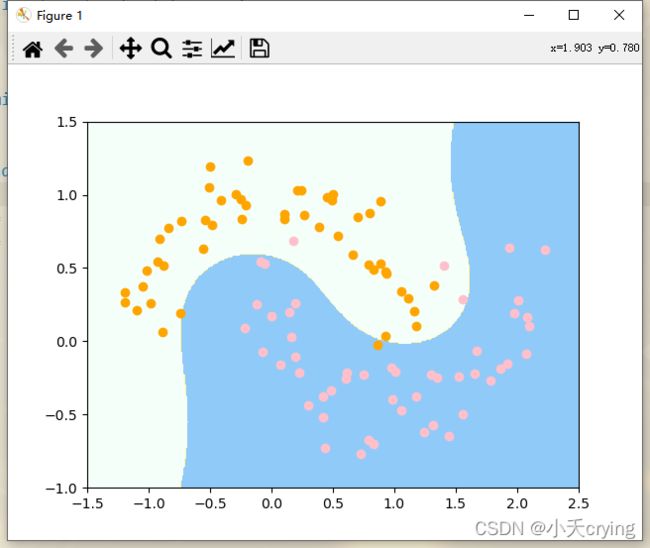
使用多项式特征的SVM算法相当于先对数据转换为高维的、有特征式项的数据，然后再扔进LinearSVC，可以采用多项式核的方式。

3、使用多项式核函数的SVM

（1）添加pipeline管道

'''
  使用多项式核函数的SVM
'''

from sklearn.svm import SVC
from sklearn.pipeline import Pipeline # 引入Pipeline顺序执行相关过程
from sklearn.preprocessing import StandardScaler # 引入多项式类、标准化

'''
  svm中使用多项式特征
  degree: 阶数
'''
def PolynomialKernelSVC(degree, C = 1.0):
  # 使用pipeline创建管道，送给实例化对象的数据会沿着管道的三步依次进行
  return Pipeline([ # Pipeline传入的是列表，列表中传入管道中每一步对应的类(这个类以元组的形式进行传送)
    ("std_scaler", StandardScaler()), # 第一步：数值的均一化
    ("kernelSVC", SVC(kernel='poly', degree=degree, C=C)) # 第二步：进行训练(同样可以达到多项式SVM的效果)
  ])

（2）生成样本，实例化对象

from sklearn import datasets

X, y = datasets.make_moons(noise=0.15, random_state=666)
# 实例化对象
poly_kernel_svc = PolynomialKernelSVC(degree=3)
poly_kernel_svc.fit(X, y)

（3）绘制决策边界

import numpy as np
import matplotlib.pyplot as plt

plot_decision_boundary(poly_kernel_svc, axis=[-1.5, 2.5, -1.0, 1.5])
# 绘制样本
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()

其中plot_decision_boundary函数

'''
  绘制决策边界
  params-model:训练好的model
  params-axis:绘制区域坐标轴范围（0,1,2,3对应x轴和y轴的范围）
'''
def plot_decision_boundary(model, axis):
  # meshgrid:生成网格点坐标矩阵
  x0, x1 = np.meshgrid(
    # 通过linspace把x轴分成无数点
    # axis[1] - axis[0]是x的左边界减去x的右边界
    # axis[3] - axis[2]：y的最大值减去y的最小值
        
    # arr.shape    # (a,b)
    # arr.reshape(m,-1) #改变维度为m行、d列 （-1表示列数自动计算，d= a*b /m）
    # arr.reshape(-1,m) #改变维度为d行、m列 （-1表示行数自动计算，d= a*b /m ）
    np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
    np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
  )
  print('x0', x0)
  # print('x1', x1)
  # np.r_是按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等，相加后列数不变。
  # np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等，相加后行数不变。
  # .ravel():将多维数组转换为一维数组
  X_new = np.c_[x0.ravel(), x1.ravel()]
  y_predict = model.predict(X_new)
  
  # 这里不能zz = y_predict.reshape(x0.shape)，会报错'list' object has no attribute 'reshape'
  # 要通过np.array转换一下
  zz = np.array(y_predict).reshape(x0.shape)

  from matplotlib.colors import ListedColormap
  # ListedColormap允许用户使用十六进制颜色码来定义自己所需的颜色库，并作为plt.scatter()中的cmap参数出现：
  custom_cmap = ListedColormap(['#F5FFFA', '#FFF59D', '#90CAF9'])
  # coutourf([X, Y,] Z,[levels], **kwargs),contourf画的是登高线之间的区域
  # Z是和X,Y相同维数的数组。
  plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

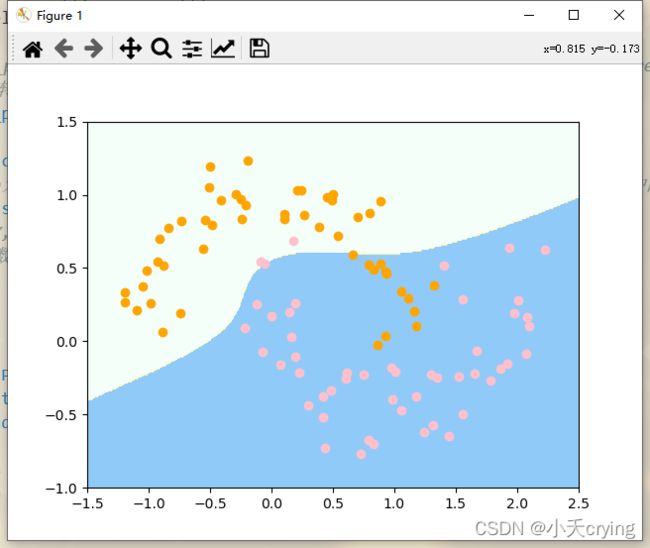
虽然这个决策边界和使用多项式SVM的决策边界不一样，但是这依然是非线性决策边界
上述的方法通过SVC，在kernel中传入poly这个参数然后再进行SVM的过程，就是通过多项式核函数进行SVM的过程

5、sklearn中的RBF核（高斯核）

（1）生成样本

'''
  sklearn中的高斯核函数（RBF核）
'''
import numpy as np
import matplotlib.pyplot as plt

from sklearn import datasets

X, y = datasets.make_moons(noise=0.15, random_state=666)

# 绘制样本
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()

（2）添加pipeline管道

'''
  svm中使用高斯核
  degree: 阶数
'''
def RBFkernelSVC(gamma=1.0):
  # 使用pipeline创建管道，送给实例化对象的数据会沿着管道的两步步依次进行
  return Pipeline([ # Pipeline传入的是列表，列表中传入管道中每一步对应的类(这个类以元组的形式进行传送)
    ("std_scaler", StandardScaler()), # 第一步：数值的均一化
    ("svc", SVC(kernel='rbf', gamma = gamma)) # 第二步：进行分类,使用RBF高斯核
  ])

（3）实例化对象进行训练

# 实例化svc对象
svc = RBFkernelSVC(gamma=1.0)
# 这里仍然不区分训练集与测试集，只是直观的观察效果(gamma的值改变的效果)
svc.fit(X, y)

（4）绘制决策边界

plot_decision_boundary(svc, axis=[-1.5, 2.5, -1.0, 1.5])

其中这个函数如下

'''
  绘制决策边界
  params-model:训练好的model
  params-axis:绘制区域坐标轴范围（0,1,2,3对应x轴和y轴的范围）
'''
def plot_decision_boundary(model, axis):
  # meshgrid:生成网格点坐标矩阵
  x0, x1 = np.meshgrid(
    # 通过linspace把x轴分成无数点
    # axis[1] - axis[0]是x的左边界减去x的右边界
    # axis[3] - axis[2]：y的最大值减去y的最小值
        
    # arr.shape    # (a,b)
    # arr.reshape(m,-1) #改变维度为m行、d列 （-1表示列数自动计算，d= a*b /m）
    # arr.reshape(-1,m) #改变维度为d行、m列 （-1表示行数自动计算，d= a*b /m ）
    np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
    np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
  )
  # print('x0', x0)
  # print('x1', x1)
  # np.r_是按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等，相加后列数不变。
  # np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等，相加后行数不变。
  # .ravel():将多维数组转换为一维数组
  X_new = np.c_[x0.ravel(), x1.ravel()]
  y_predict = model.predict(X_new)
  
  # 这里不能zz = y_predict.reshape(x0.shape)，会报错'list' object has no attribute 'reshape'
  # 要通过np.array转换一下
  zz = np.array(y_predict).reshape(x0.shape)

  from matplotlib.colors import ListedColormap
  # ListedColormap允许用户使用十六进制颜色码来定义自己所需的颜色库，并作为plt.scatter()中的cmap参数出现：
  custom_cmap = ListedColormap(['#F5FFFA', '#FFF59D', '#90CAF9'])
  # coutourf([X, Y,] Z,[levels], **kwargs),contourf画的是登高线之间的区域
  # Z是和X,Y相同维数的数组。
  plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

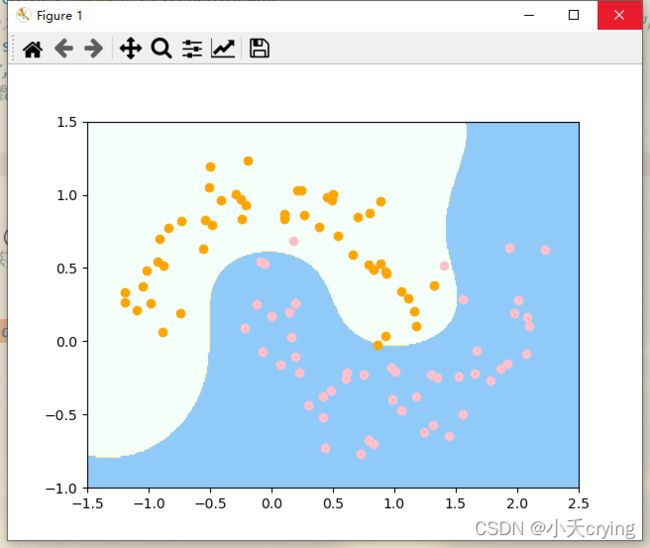
以上的情况是gamma取1.0时候的值。下面改变gamma的值
1）gamma=1

2）gamma=100

# 实例化svc对象
svc_gamma100 = RBFkernelSVC(gamma=100)
# 这里仍然不区分训练集与测试集，只是直观的观察效果(gamma的值改变的效果)
svc_gamma100.fit(X, y)
plot_decision_boundary(svc_gamma100, axis=[-1.5, 2.5, -1.0, 1.5])
# 绘制
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()

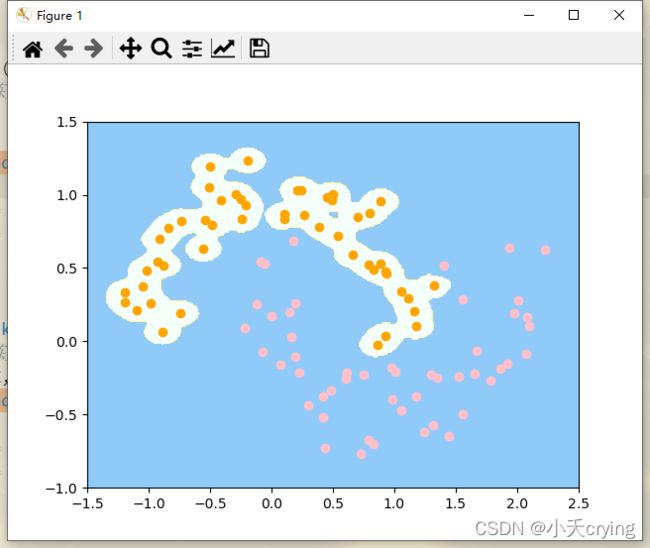
回忆一下这一块在svm理论分析中的分析，gamma的值越大，σ越小，正态分布的图像越窄

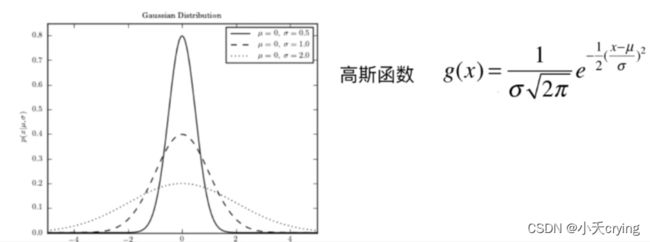
当我们使用高斯核之后，增大gamma，相当于针对其中某一类，针对这一类，其中每一个样本点，在他的周围都形成了正态分布的情况（可以想象我们现在是俯视正态分布的图形，对于上图中橘色的点，对于每一个点而言，都对应俯视这个高斯分布图形对应的那个尖尖，由于gamma比较大，所以高斯分布比较窄，所以俯视看上去就是在每一个橘色的点周围围绕了一定的区域，只在这个区域内我们把它判定成橘色的点，否则我们都把他判定成蓝色的点）
这样的结果显然是过拟合了，他过于和当前数据集是什么样子相关了。
3）gamma=10

# 实例化svc对象
svc_gamma10 = RBFkernelSVC(gamma=10)
# 这里仍然不区分训练集与测试集，只是直观的观察效果(gamma的值改变的效果)
svc_gamma10.fit(X, y)
plot_decision_boundary(svc_gamma10, axis=[-1.5, 2.5, -1.0, 1.5])
# 绘制
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()

减小gamma到10，可以看到相对于gamma=100的情况，对于每个橘色的点来说，高斯分布的图案相对于变得更宽了一些，从俯视的角度来看，橘色点周围的区域变得更宽了，当橘色和橘色点之间距离比较近的时候，他们的区域就融合在了一起，形成了这样的决策边界。
现在回过头来看，gamma=1的时候，高斯分布的更加宽，从俯视图的角度来看，每个橘色点周围的区域更加宽了，当橘色和橘色点之间距离比较近的时候，他们的区域就融合在一起之后的整个区域更加大了。
接下来把gamma降低到0.5
4）gamma=0.5

# 实例化svc对象
svc_gamma05 = RBFkernelSVC(gamma=0.5)
# 这里仍然不区分训练集与测试集，只是直观的观察效果(gamma的值改变的效果)
svc_gamma05.fit(X, y)
plot_decision_boundary(svc_gamma05, axis=[-1.5, 2.5, -1.0, 1.5])
# 绘制
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()

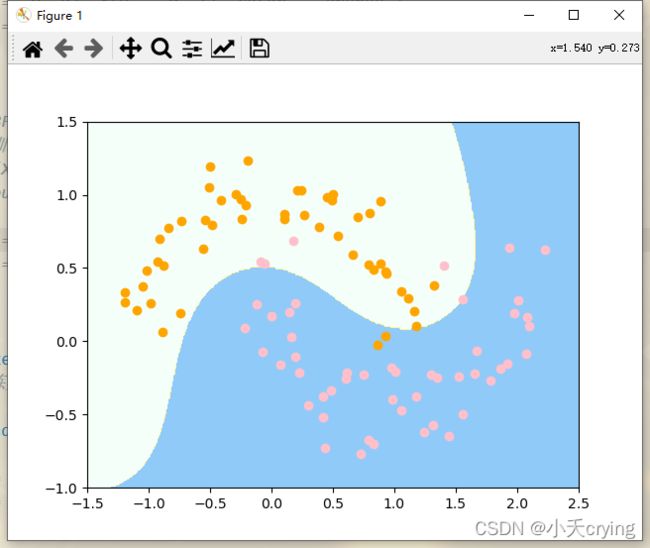
现在橘色点对应的分类区域变得更加大了
继续减小gamma
5）gamma=0.1

# 实例化svc对象
svc_gamma01 = RBFkernelSVC(gamma=0.1)
# 这里仍然不区分训练集与测试集，只是直观的观察效果(gamma的值改变的效果)
svc_gamma01.fit(X, y)
plot_decision_boundary(svc_gamma01, axis=[-1.5, 2.5, -1.0, 1.5])
# 绘制
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()

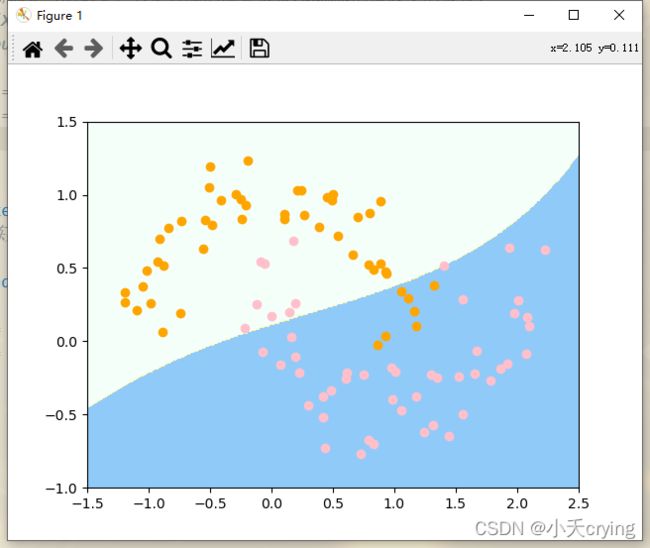
此时这个决策边界已经接近线性的决策边界了。这时已经是欠拟合的状态了，不能非常好的反映出数据的分类样子，泛化能力非常低。

（5）总结
当我们使用高斯核的时候，我们的gamma值相当于是在调整模型复杂度，gamma值越小，模型复杂度越低，模型越倾向于欠拟合；gamma值越高，模型复杂度越高，模型越倾向于过拟合。在实际情况使用的时候要找到一个最佳的gamma值