Unity3D C#数学系列之求点到直线的距离

---

1. 引言

之前写的博客里面有好多坑没有填，以后慢慢填吧。
最近想到可以总结点和数学相关的东西，自己觉得挺有意思的。目前想到的可以总结点有：

• 求空间中一点到两点所在直线的距离
• 求空间过一点到两点所在直线的垂线
• 求两条直线的交点
• 已知一个圆，并给出圆上一点，求该点在圆上的切线
• 求三点所在平面的法线方向
• 判断一点是否在圆弧范围内
• 判断一点是否在矩形内部
• 判断一点是否在长方体、球体、圆柱体内部
• 网格绘制长方体、球体、胶囊体

这里，我们先看看"求空间中一点到两点所在直线的距离"。
这里给出两种方法来计算，我测试了下，其实两种方式的效率差不多。

2. 法一(角度法)

2.1 分析

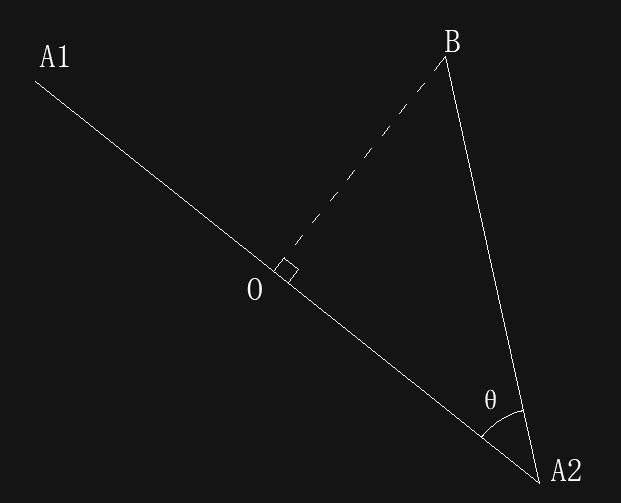
如图，已知A1、A2、B点的坐标，求B点到A1A2所在直线的距离，即BO的长度。
分析：

1. 三个点的坐标已知，则BA2这条线段的长度已知，在代码中直接使用Vector3.Distance即可
2. 同时A2A1、A2B这两条向量也能求出，则θ的角度值也能求出，在代码中使用点积即可
3. 那么，BO = |A2B|*sinθ

2.2 代码

2.2.1 求两点的距离

直接使用Vector3.Distance，即可求出。

float distance = Vector3.Distance(a, b);

2.2.2 向量的点积求夹角

直接看公式。

分解一下，要求到θ，需要以下几个步骤

• 求点积，两个坐标相减求得向量，然后直接使用Vector3.Dot求得点积

Vector3 a2B = m_PointB - m_PointA2;
Vector3 a2A1 = m_PointA1 - m_PointA2;
float dotResult = Vector3.Dot(a2B, a2A1);

• 求向量的模，直接使用Vector3.magnitude即可，如

a2B.magnitude

• 反Cos求出θ，直接使用Matfh.Acos

float seitaRad = Mathf.Acos(dotResult / (a2B.magnitude * a2A1.magnitude));

这里有一点要注意，Mathf.Acos求出的θ是用弧度值(rad)表示的，弧度值和我们平时喜欢用的0°、180°的关系是
Π弧度 = 180°
如下表

度	0°	90°	180°	270°	360°
弧度	0	Π/2	Π	3Π/2	2Π

在代码中弧度值和角度值的换算直接乘以Mathf.Rad2Deg(弧度值转换为角度值，2表示to的意思)或Mathf.Deg2Rad(角度值转换为弧度值)，如下。

// 弧度值转换为角度值
float angle = seitaRad * Mathf.Rad2Deg;
// 角度值转换为弧度值
float rad = angle * Mathf.Deg2Rad;

2.2.3 完整代码

private float DistanceFromPoint2Line(Vector3 p, Vector3 p1, Vector3 p2)
{
    // 求A2B的距离
    float p2pDistance = Vector3.Distance(p2, p);    // 或者使用 p2p.magnitude
    Vector3 p2p1 = p2 - p1;
    Vector3 p2p = p2 - p;
    // 求p2p1·p2p
    float dotResult = Vector3.Dot(p2p1, p2p);
    // 求θ
    float seitaRad = Mathf.Acos(dotResult / (p2p1.magnitude * p2pDistance));
    // 求p点到p1p2的距离
    float distance = p2pDistance * Mathf.Sin(seitaRad);
    return distance;
}

3. 法二(面积法)

3.1 分析

如图，我们先做条辅助线，A₂A₁^’，A₂A₁^’与A₂A₁互相垂直。

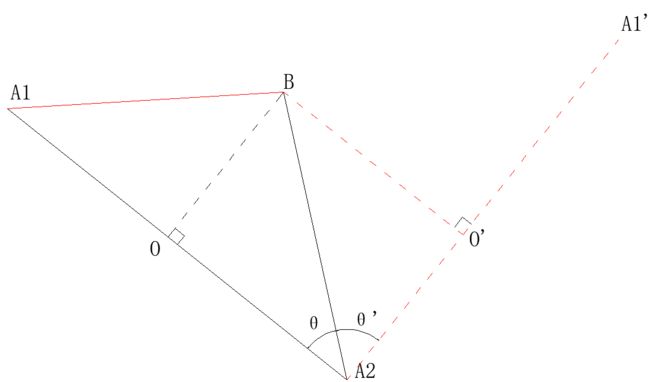
然后我们求出通过计算A₂A₁^’与A₂B的点积就可求出BO的距离。
具体分析如下：

其中不正好是A₁A₂B面积的两倍么，这也是这个方法为啥叫面积法的原因。
根据上面的分析，我们只需要求出即可。
那怎么求？
我们可以把它看做是绕着A₁A₂B所在平面的法线旋转90°后得到的。
A₁A₂B所在平面的法线怎么求？
很简单，直接用向量的叉积(两个向量的叉积得到的结果就是两个向量所在平面的法线)。

3.2 代码

// 法二 面积法
/// 

/// 面积法求点到直线的距离.
/// 
/// 待求点.
/// 直线端点
/// 直线端点
/// 
private float DistanceByArea(Vector3 pB, Vector3 pA1, Vector3 pA2)
{
    Vector3 a2A1 = pA1 - pA2;
    Vector3 a2B = pB - pA2;

    Vector3 normal = Vector3.Cross(a2A1, a2B);
    Vector3 a2A1Temp = Vector3.Cross(a2A1, normal).normalized;

    return Mathf.Abs(Vector3.Dot(a2B, a2A1Temp));
}

4 项目

效果如下。

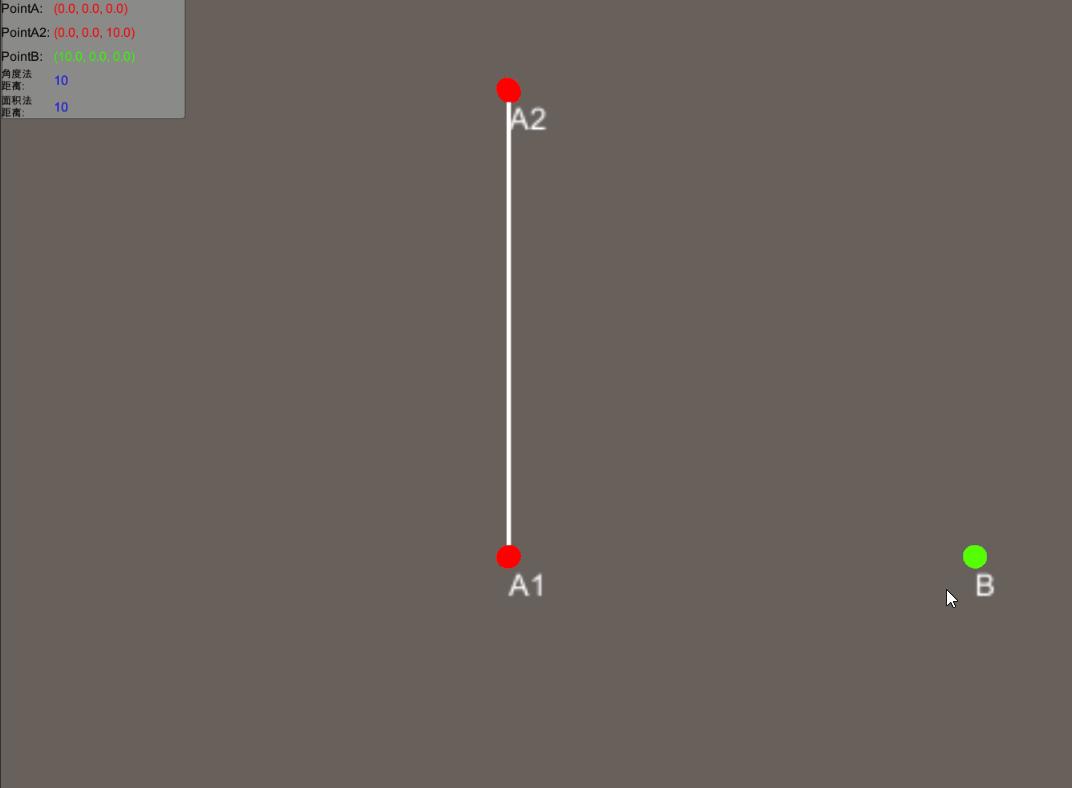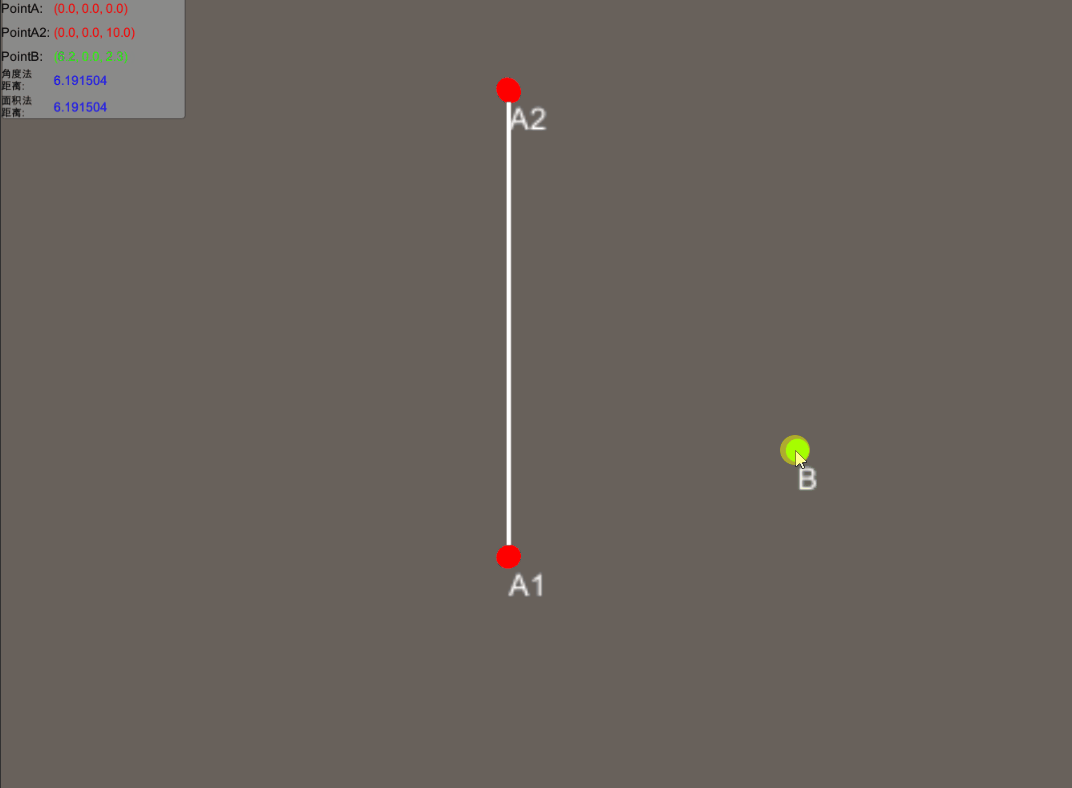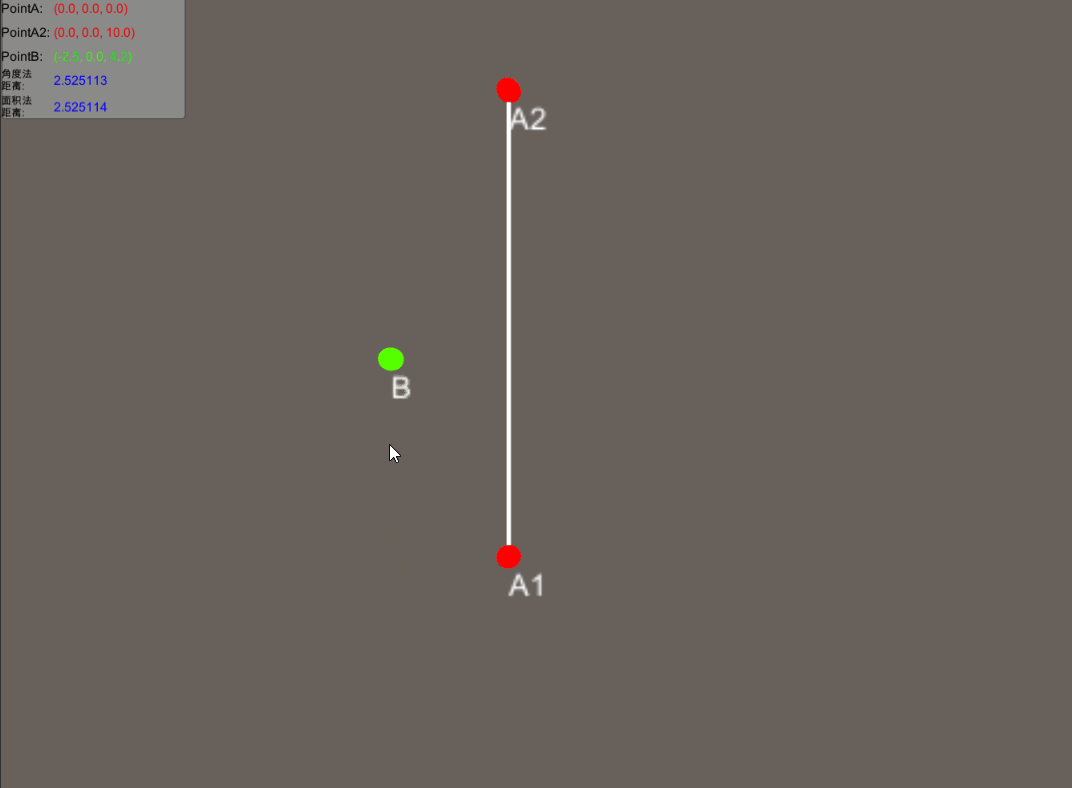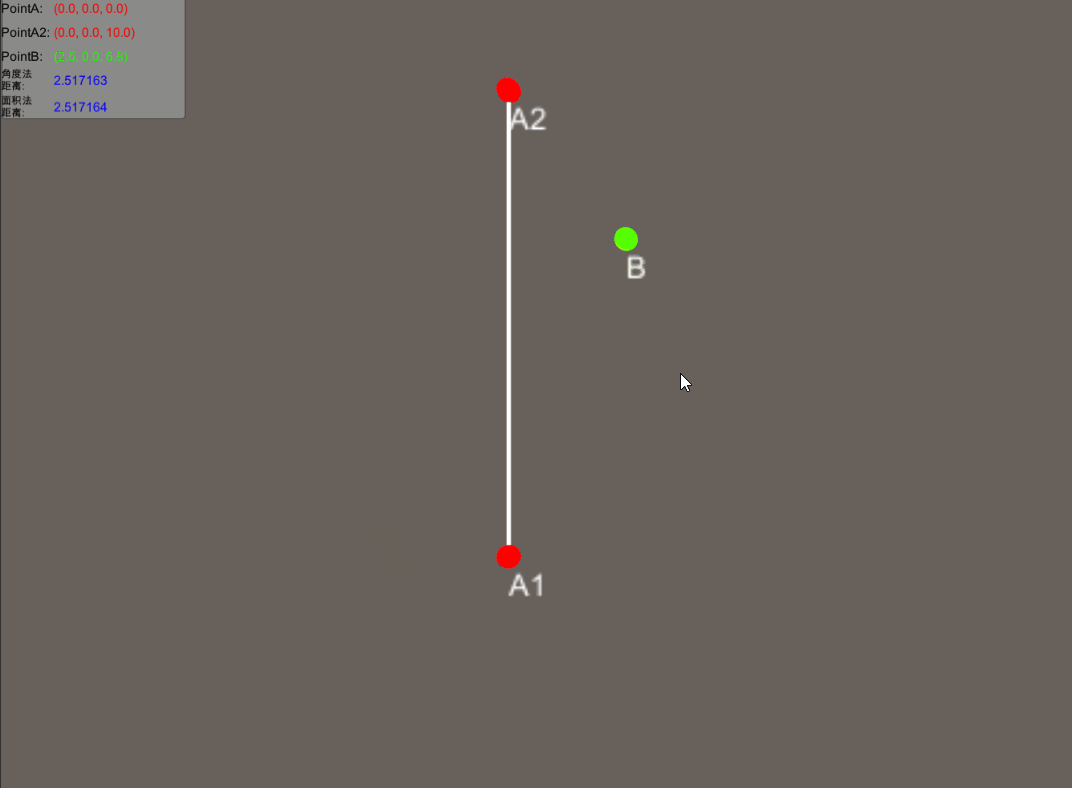
这次我们仅仅求到了BO的距离，那可否将O点的位置也求出来呢？当然是可以的。
因为OB的长度都求到了，同理可求得OA₂的距离（OA₂=|BA₂|）或者直接使用勾股定理，然后由于A₂A₁的方向已知，所以O点的坐标 = A₂+A₂A₁的单位向量*|OB|即可。
项目上传到这里啦。
链接：https://pan.baidu.com/s/1JOj41DJGwDr16G5OkAaQng
提取码：okcd
博主个人博客本文链接。