力扣-第 236 场周赛

本文旨在对于笔者日常比赛的整理复盘，如果有不足的地方，欢迎大家在评论区指出

---

Question one: 数组元素积的符号

已知函数 signFunc(x) 将会根据 x 的正负返回特定值：

如果 x 是正数，返回 1 。
如果 x 是负数，返回 -1 。
如果 x 是等于 0 ，返回 0 。
给你一个整数数组 nums 。令 product 为数组 nums 中所有元素值的乘积。

返回 signFunc(product) 。

示例 1：

输入：nums = [-1,-2,-3,-4,3,2,1]
输出：1
解释：数组中所有值的乘积是 144 ，且 signFunc(144) = 1

示例 2：

输入：nums = [1,5,0,2,-3]
输出：0
解释：数组中所有值的乘积是 0 ，且 signFunc(0) = 0

示例 3：

输入：nums = [-1,1,-1,1,-1]
输出：-1
解释：数组中所有值的乘积是 -1 ，且 signFunc(-1) = -1

提示：

• 1 <= nums.length <= 1000
• -100 <= nums[i] <= 100

题目链接

题目分析

这道题由于数据范围的原因，如果直接乘起来long都存储不下，我的思路是统计负数的个数，如果为奇数，那么返回-1，否则返回1

解题代码

Java

class Solution {
    public int arraySign(int[] nums) {
        int n = nums.length;
        
        int cnt = 0; // 用于统计负数的个数
        for(int i=0; i<n; i++){
            if(nums[i]==0) return 0;
            if(nums[i]<0) cnt += 1;
        }
        if(cnt%2==0) return 1;
        return -1;
    }
}

---

Question two: 找出游戏的获胜者

共有 n 名小伙伴一起做游戏。小伙伴们围成一圈，按 顺时针顺序 从 1 到 n 编号。确切地说，从第 i 名小伙伴顺时针移动一位会到达第 (i+1) 名小伙伴的位置，其中 1 <= i < n ，从第 n 名小伙伴顺时针移动一位会回到第 1 名小伙伴的位置。

游戏遵循如下规则：

从第 1 名小伙伴所在位置 开始 。
沿着顺时针方向数 k 名小伙伴，计数时需要 包含 起始时的那位小伙伴。逐个绕圈进行计数，一些小伙伴可能会被数过不止一次。
你数到的最后一名小伙伴需要离开圈子，并视作输掉游戏。
如果圈子中仍然有不止一名小伙伴，从刚刚输掉的小伙伴的 顺时针下一位 小伙伴 开始，回到步骤 2 继续执行。
否则，圈子中最后一名小伙伴赢得游戏。
给你参与游戏的小伙伴总数 n ，和一个整数 k ，返回游戏的获胜者。
示例 1：

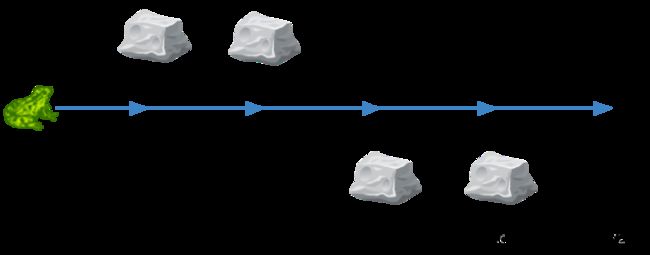
输入：n = 5, k = 2
输出：3
解释：游戏运行步骤如下：
1) 从小伙伴 1 开始。
2) 顺时针数 2 名小伙伴，也就是小伙伴 1 和 2 。
3) 小伙伴 2 离开圈子。下一次从小伙伴 3 开始。
4) 顺时针数 2 名小伙伴，也就是小伙伴 3 和 4 。
5) 小伙伴 4 离开圈子。下一次从小伙伴 5 开始。
6) 顺时针数 2 名小伙伴，也就是小伙伴 5 和 1 。
7) 小伙伴 1 离开圈子。下一次从小伙伴 3 开始。
8) 顺时针数 2 名小伙伴，也就是小伙伴 3 和 5 。
9) 小伙伴 5 离开圈子。只剩下小伙伴 3 。所以小伙伴 3 是游戏的获胜者。

示例 2：

输入：n = 6, k = 5
输出：1
解释：小伙伴离开圈子的顺序：5、4、6、2、3 。小伙伴 1 是游戏的获胜者。

提示

• 1 <= k <= n <= 500

题目链接

题目分析

这道题其实是约瑟夫环问题的裸题，对于约瑟夫环问题，是可以通过递推推出来的，这里我先简要介绍一下DP的做法，我们定义f[n, k]表示n个人，每一次数到第k个人时淘汰掉一个最终剩下的人的编号，我们发现当淘汰掉第k个人之后，第k+1个人的编号原本为k现在变为0，也就是状态f[n-1, k]最终剩下人的编号加上k再模n就是它在原先n个人时的编号，所对应的状态转移方程为f[n, k] = (f[n-1, k]+k)%n，这样我们从最基础的情况开始看，当只有一个人的时候，最终剩下人的编号为0，那么这个剩下的人在两个人的时候的编号就是(0+k)%2，以此类推，我们就可以得出n个人的时候最终剩下的人的编号

解题代码

Java

class Solution {
    public int findTheWinner(int n, int k) {
        int st = 0;
        for(int i=2; i<=n; i++){
            st = (st + k) % i;
        }
        return st+1;
    }
}

---

Question three: 最少侧跳次数

给你一个长度为 n 的 3 跑道道路 ，它总共包含 n + 1 个 点 ，编号为 0 到 n 。一只青蛙从 0 号点第二条跑道 出发 ，它想要跳到点 n 处。然而道路上可能有一些障碍。

给你一个长度为 n + 1 的数组 obstacles ，其中 obstacles[i] （取值范围从 0 到 3）表示在点 i 处的 obstacles[i] 跑道上有一个障碍。如果 obstacles[i] == 0 ，那么点 i 处没有障碍。任何一个点的三条跑道中 最多有一个 障碍。

比方说，如果 obstacles[2] == 1 ，那么说明在点 2 处跑道 1 有障碍。
这只青蛙从点 i 跳到点 i + 1 且跑道不变的前提是点 i + 1 的同一跑道上没有障碍。为了躲避障碍，这只青蛙也可以在 同一个 点处 侧跳 到 另外一条 跑道（这两条跑道可以不相邻），但前提是跳过去的跑道该点处没有障碍。

比方说，这只青蛙可以从点 3 处的跑道 3 跳到点 3 处的跑道 1 。
这只青蛙从点 0 处跑道 2 出发，并想到达点 n 处的 任一跑道 ，请你返回 最少侧跳次数 。

注意：点 0 处和点 n 处的任一跑道都不会有障碍。
示例 1：

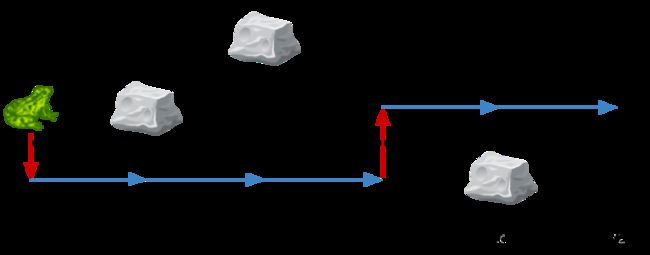
输入：obstacles = [0,1,2,3,0]
输出：2 
解释：最优方案如上图箭头所示。总共有 2 次侧跳（红色箭头）。
注意，这只青蛙只有当侧跳时才可以跳过障碍（如上图点 2 处所示）。

示例二：

输入：obstacles = [0,1,1,3,3,0]
输出：0
解释：跑道 2 没有任何障碍，所以不需要任何侧跳。

示例 3：

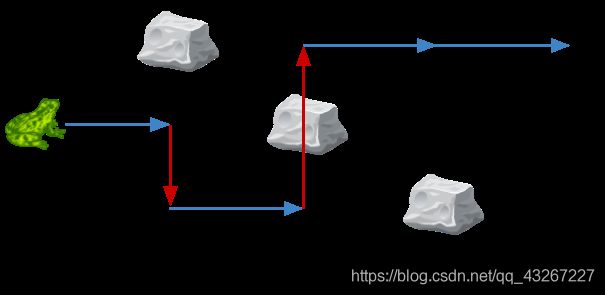
输入：obstacles = [0,2,1,0,3,0]
输出：2
解释：最优方案如上图所示。总共有 2 次侧跳。

提示：

• obstacles.length == n + 1
• 1 <= n <= 5 * 10^5
• 0 <= obstacles[i] <= 3
• obstacles[0] == obstacles[n] == 0

题目链接

题目分析

这道题可以使用动态规划来做，我们定义f[i, j]表示第i个节点，在第j条跑道上的最少侧跳次数，那么我们的状态转移方程就可以定义为f[i, j] = min(f[i, j], f[i-1, j] + cost)，其中cost指的是从三条跑道跳到该跑道的消耗，它的取值有两种情况，当青蛙此时在当前跑道，那么cost为0，否则cost为1，由于最终到哪条跑道都是可以的，所以最终我们要返回三条跑道的最小值

解题代码

Java

class Solution {
    static int INF = 0x3f3f3f3f;
    public int minSideJumps(int[] obstacles) {
        /**
        f[i, j]表示在第i个点，第j条跑道上的最少侧跳次数
        f[0, 1] = 0  f[0][0]=f[0][2] = 1
        **/
        
        int n = obstacles.length;
        int[][] f = new int[n][3];
        f[0][1] = 0; f[0][0] = f[0][2] = 1;
        
        n -= 1;
        for(int i=1; i<=n; i++){
            for(int j=0; j<3; j++){
                f[i][j] = INF;
                if(j == obstacles[i]-1) continue; // 如果当前跑道有障碍，就无需计算
                for(int k=0; k<3; k++){ // 枚举跳到该跑道的中间跑道
                    if(k == obstacles[i]-1) continue; // 如果中间跑道有障碍，则无需计算
                    int cost = 0;
                    if(k != j) cost = 1;
                    f[i][j] = Math.min(f[i][j], f[i-1][k]+cost);
                }
            }
        }
        return Math.min(f[n][0], Math.min(f[n][1], f[n][2]));
    }
}

---

Question four: 求出 MK 平均值

给你两个整数 m 和 k ，以及数据流形式的若干整数。你需要实现一个数据结构，计算这个数据流的 MK 平均值 。

MK 平均值 按照如下步骤计算：

如果数据流中的整数少于 m 个，MK 平均值 为 -1 ，否则将数据流中最后 m 个元素拷贝到一个独立的容器中。
从这个容器中删除最小的 k 个数和最大的 k 个数。
计算剩余元素的平均值，并 向下取整到最近的整数 。
请你实现 MKAverage 类：

MKAverage(int m, int k) 用一个空的数据流和两个整数 m 和 k 初始化 MKAverage 对象。
void addElement(int num) 往数据流中插入一个新的元素 num 。
int calculateMKAverage() 对当前的数据流计算并返回 MK 平均数 ，结果需 向下取整到最近的整数 。

示例 1：

输入：
["MKAverage", "addElement", "addElement", "calculateMKAverage", "addElement", "calculateMKAverage", "addElement", "addElement", "addElement", "calculateMKAverage"]
[[3, 1], [3], [1], [], [10], [], [5], [5], [5], []]
输出：
[null, null, null, -1, null, 3, null, null, null, 5]

解释：
MKAverage obj = new MKAverage(3, 1); 
obj.addElement(3);        // 当前元素为 [3]
obj.addElement(1);        // 当前元素为 [3,1]
obj.calculateMKAverage(); // 返回 -1 ，因为 m = 3 ，但数据流中只有 2 个元素
obj.addElement(10);       // 当前元素为 [3,1,10]
obj.calculateMKAverage(); // 最后 3 个元素为 [3,1,10]
                          // 删除最小以及最大的 1 个元素后，容器为 [3]
                          // [3] 的平均值等于 3/1 = 3 ，故返回 3
obj.addElement(5);        // 当前元素为 [3,1,10,5]
obj.addElement(5);        // 当前元素为 [3,1,10,5,5]
obj.addElement(5);        // 当前元素为 [3,1,10,5,5,5]
obj.calculateMKAverage(); // 最后 3 个元素为 [5,5,5]
                          // 删除最小以及最大的 1 个元素后，容器为 [5]
                          // [5] 的平均值等于 5/1 = 5 ，故返回 5

提示：

• 3 <= m <= 10^5
• 1 <= k*2 < m
• 1 <= num <= 10^5
• addElement 与 calculateMKAverage 总操作次数不超过 10^5 次。

题目链接

题目分析

笔者的个人能力有限，第四题暂时给不出解法，请大家谅解!!!