前言
本篇文章包含以下内容:
- 1、球体绘制
- 2、纹理映射到球体
- 3、球体自转
先来看下最终效果:
地球仪
1、球体绘制
1.1 数学模型分析
球体坐标数学模型
根据上述球体数学模型可以计算出球体的顶点坐标:
设球体半径为r、∠EOD为u、∠AOB为v,这样我们可以计算出(x, y, z)坐标
y = r * cosu
线段OB = r * sinu
x = OB * sinv
z = OB * cosv
计算得出:===>
x = r * sinu * sinv
y = r * cosu
z = r * sinu * cosv
如果这里的角u、v不好理解,可以把u、v想象成经纬度,u代表纬度,v代表经度
1.2 代码实现
- 1、根据角度u、v计算球面上的顶点坐标
typedef struct {
GLKVector3 positionCoord; // 顶点坐标
} SenceVertex;
- (SenceVertex)caculateCoordinate:(GLfloat)u v:(GLfloat)v {
GLfloat r = 1.0;
GLfloat pi = M_PI;
GLfloat y = r * cos(pi * u);
GLfloat x = r * sin(pi * u) * sin(2 * pi * v);
GLfloat z = r * sin(pi * u) * cos(2 * pi * v);
return (SenceVertex){{x, y ,z}};
}
因为OpenGL的顶点坐标取值范围[-1, 1],所以这里的球体半径取值
r=1
-
2、将“经纬度”u,v等分,构造球体顶点坐标数组
u取值范围[0, 180],v取之范围[0, 360]
- (void)generateWithVertices:(SenceVertex *)vertices numOfU:(GLuint)numOfU numOfV:(GLuint)numOfV {
GLfloat uStep = 1.0 / numOfU;
GLfloat vStep = 1.0 / numOfV;
GLint offset = 0;
for (int u = 0; u < numOfU; u++) {
for (int v = 0; v < numOfV; v++) {
SenceVertex point1 = [self caculateCoordinate:u * uStep v:v * vStep];
SenceVertex point2 = [self caculateCoordinate:(u + 1) * uStep v:v * vStep];
SenceVertex point3 = [self caculateCoordinate:(u + 1) * uStep v:(v + 1) * vStep];
SenceVertex point4 = [self caculateCoordinate:u * uStep v:(v + 1) * vStep];
self.vertices[offset] = point1;
self.vertices[offset + 1] = point4;
self.vertices[offset + 2] = point3;
self.vertices[offset + 3] = point1;
self.vertices[offset + 4] = point3;
self.vertices[offset + 5] = point2;
offset += 6;
}
}
}
这里使用六个顶点绘制三角形△ABC和△ACD(按照顺时针,3D中使用顺时针和逆时针来区分正面和背面),如下图示意:
绘制三角形
-
3、创建球体顶点坐标数据
这里将u进行30等分,v60等分,创建球体顶点坐标(如果需要高精度绘制,可以增大等分量)
GLuint numOfU = 30;
GLuint numOfV = 60;
self.vertices = malloc(sizeof(SenceVertex) * numOfU * numOfV * 6);
[self generateWithVertices:self.vertices numOfU:numOfU numOfV:numOfV];
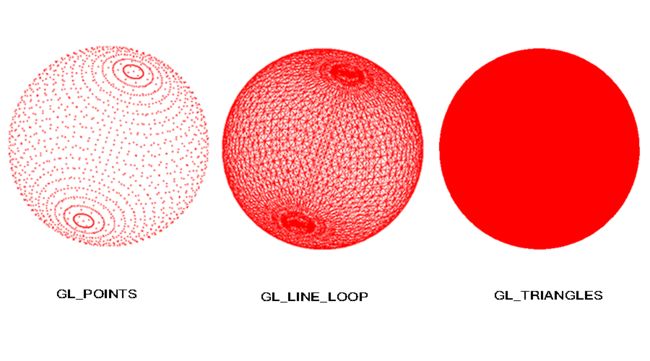
- 4、分别使用GL_POINTS、GL_LINE_LOOP、GL_TRIANGLES模式绘制,效果如下:
这里使用缺省顶点着色器和片元着色器(为了看起来立体,在mvp中的模型矩阵添加了60度的旋转)
2、纹理渲染映射到球体
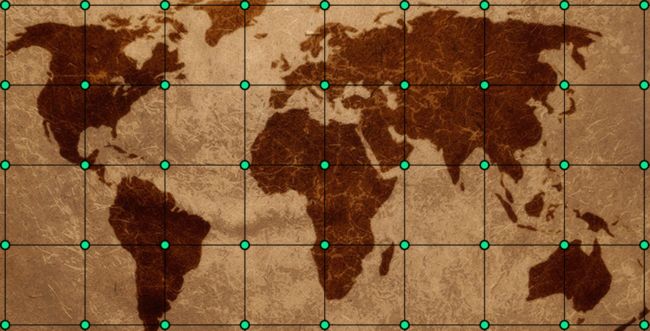
和球体顶点一样,对原始图片分别对x、y轴进行等分,每个顶点对应一个纹理坐标
v对应x轴的等分,u对应y轴等分
typedef struct {
GLKVector3 positionCoord; // 顶点坐标
GLKVector2 textureCoord; // 纹理坐标
} SenceVertex;
- (SenceVertex)caculateCoordinate:(GLfloat)u v:(GLfloat)v {
GLfloat r = 1.0;
GLfloat pi = M_PI;
GLfloat y = r * cos(pi * u);
GLfloat x = r * sin(pi * u) * sin(2 * pi * v);
GLfloat z = r * sin(pi * u) * cos(2 * pi * v);
return (SenceVertex){{x, y ,z}, {v, u}};
}
可以参考如下示意图:
3、球体自转
使用CADisplayLink,实时更新到mvp矩阵中的模型矩阵,对y轴进行角度旋转,产生自转效果
// 矩阵变换
// 正交投影矩阵
GLKMatrix4 project = GLKMatrix4MakeOrtho(-1.0, 1.0, -1.0, 1.0, 0.1, 100.0);
// 观察矩阵
GLKMatrix4 view = GLKMatrix4MakeLookAt(0.0, 0.0, 3.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);
// 模型矩阵
GLKMatrix4 model = GLKMatrix4Identity;
model = GLKMatrix4Rotate(model, GLKMathDegreesToRadians(angle), 0.0, 1.0, 0.0);
GLKMatrix4 mvp = GLKMatrix4Identity;
mvp = GLKMatrix4Multiply(mvp, project);
mvp = GLKMatrix4Multiply(mvp, view);
mvp = GLKMatrix4Multiply(mvp, model);
最终效果见开头⬆️
源码
请到Github上查看完整代码。
参考
- OpenGL ES之纹理渲染
- GL02-02:OpenGL球体绘制
更佳阅读体验,请访问原文地址:OpenGL-ES之旋转的地球