原作者:https://www.cnblogs.com/aipufu/p/11596253.html
https://www.cnblogs.com/leezx/p/5590159.html
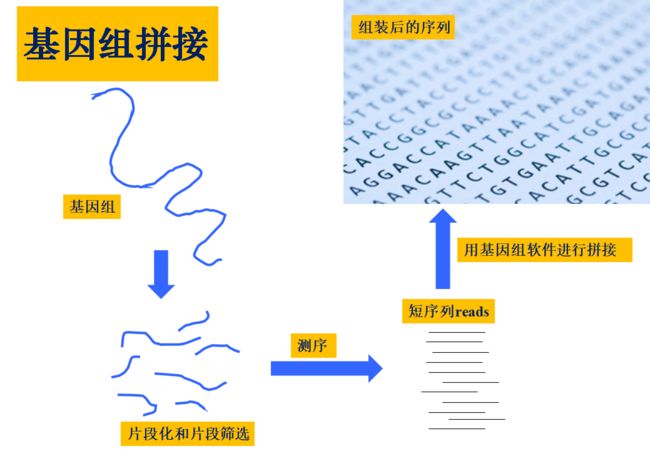
每一个物种的参考基因组序列(reference genome)的产生都要先通过测序的方法,获得基因组的测序读段(reads),然后再进行从头拼接或组装(英文名称为do novo genome assembly),最后还原测序物种的各条染色体的序列,即ATGC四种碱基的排列顺序。
之所以要进行基因组拼接,是因为现在的测序技术还只能测较短的序列,无法直接获取一整条染色体的序列。如一代测序(Sanger测序)一般可测1kb左右的序列;二代测序(next-generation sequencing),一般可测50~500bp;三代测序虽然可测100kb甚至更长的序列,但现在三代测序技术还不是很成熟,还有较高的测序错误率。(欢迎关注微信公众号:AIPuFuBio,和使用生物信息学平台AIPuFu:www.aipufu.com)
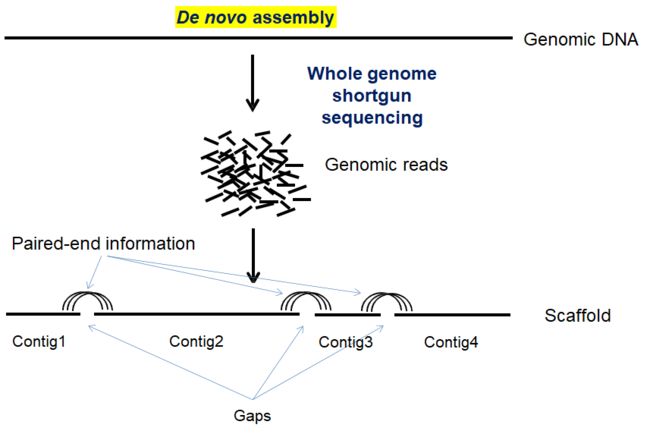
基因组测序数据的从头组装过程,可简单描述为:reads---->contig---->scaffold---->chromosome,具体如下所示:
首先基因组测序产生reads,然后对reads进行组装产生长片段Contigs,再确定Contig的方向和顺序,组装产生更长的片段Scaffolds,最后再组装连接Scaffold得到完整的染色体序列。
接下来,给大家依次介绍一下上图从头拼接中涉及到的两个概念:contig和scaffold。
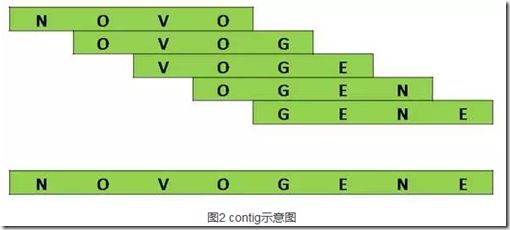
Contig是由多个reads通过组装而形成的长片段。由于测序读段较短、基因组序列通常含有较多重复序列、而且还有测序错误等原因,除了简单的基因组序列外,大部分物种的基因组序列组装都会先产生很多contig,无法一次获得完整的染色体序列。
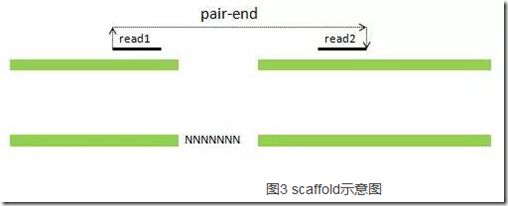
Scaffold为多条contig序列连接形成更长片段,这些contig方向和顺序已经确定,且contig间未知序列(一般用NNNN表示)的长度也获知。
Scaffold的获得一般主要通过双端测序(如paired-end sequecing或mate-pair sequencing)来确定contig的顺序和方向,以及contig之间的间隔距离,具体如下示意图所示。
基因组测序数据的从头组装的核心算法主要可以分为以下几大类:
1、基于贪心算法(greedy-extention);
2、基于Overlap-Layout-Consensus(OLC);
3、基于de Bruijn Graph;
4、以上两种或多种算法的组合;
5、其他类型。
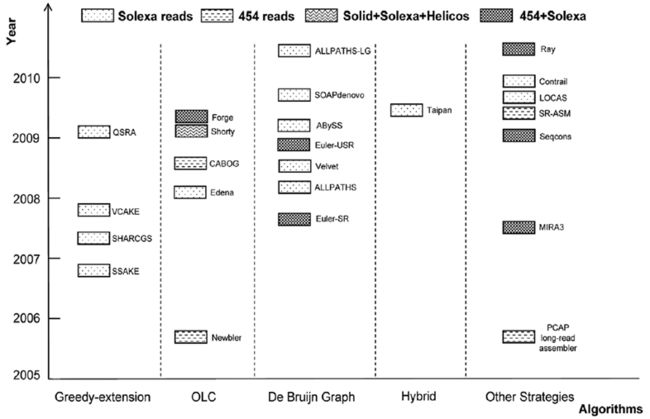
具体如下图所示:
其中最经典的两类为:
1)Overlap-Layout-Consensus(OLC)算法,基于OLC算法的组装软件主要是针对长测序读段(如Sanger测序、454测序等)设计的;
2)de Bruijn Graph算法,基于de Bruijn Graph的组装软件则主要是针对二代测序产生的短读段数据设计。
具体如下所示:
1)Overlap-Layout-Consensus(OLC)算法
2)de Bruijn Graph算法
现在主流的是二代测序技术,因此再给大家详细介绍一下专门针对二代测序数据开发的基于de Bruijn Graph的从头拼接方法。
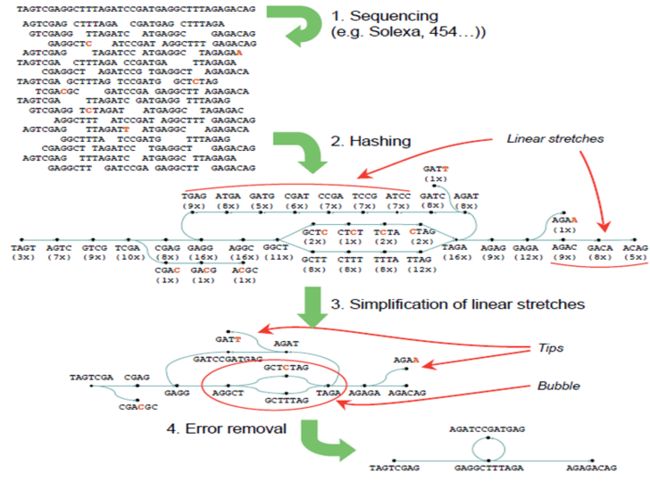
其中一个非常著名的软件就是Velvet,是基于de Bruijn Graph设计的经典代表,其算法示意图如下:
其中红色碱基为测序错误或SNP位点。
Velvet的组装原理,主要可分为这几个步骤:
1)首先把所有测序读段(reads)都分割为更小的片段k-mer;
Reads产生k-mer的过程示意图。这里k为7,假如read的长度为n,则总共可产生n-1个k-mer。
2)把每个k-mer作为一个节点,然后判断k-mer之间是否有k-1碱基的重叠,如果有则作为两个不同的节点连接起来。依次这样连接所有可连接的k-mer就形成了Velvet从头组装软件算法设计示意图中第2步的de Bruijn Graph;
3)依次合并相邻的k-mer,因为相邻的k-mer有k-1个碱基的重叠,就可进一步简化de Bruijn Graph形成Velvet从头组装软件算法设计示意图中第3步的简化后的图;
4)使用一系列算法消除由测序错误而形成的tips(具体如Velvet从头组装软件的算法设计示意图中所示),并合并bubbles(两条或多条路径序列,一般由SNP造成,如Velvet从头组装软件的算法设计示意图);
5)最后拼接得到Contig序列。
值得注意的是,Velvet从头组装软件算法设计示意图中最后一步拼接产生了回文序列,主要是由于原始序列中含有回文,如果k取为偶数(图中k=4)就容易在组装中形成这种现象。
为了有效的避免拼接中产生回文序列,一般k取为奇数。
那么基于基因组测序数据的从头拼接软件,那些具有较好的性能呢?
从上图中可以看出,Velvet和SOAPdenovo在拼接C.elegans、Yeast、E.coli、Swinepox的基因组序列时,相对于其他软件,组装结果更准确(A:Percentage of correctly mapped contigs)且拼接出来的序列能更完整的覆盖原基因组序列(B:Genome Coverage)。
DBG算法相比于OLC的优势是什么?
由于二代测序得到的reads长度较短,包含的信息量较少,因此完成基因组拼接需要较高的覆盖度。OLC算法适用于读长较长的序列组装,通过构成的OLC图寻找Consensus sequence的过程,实际上是哈密顿通路寻找的问题,算法非常复杂。
若采用OLC算法,会大大增加拼接的复杂性以及运算量。而采用DBG算法,通过K-1的overlap关系,构建DBG图,通过寻找欧拉路径得到Contig序列,从算法的角度极大的简化了组装的难度。
讲完算法,我们以目前应用广泛的 SOAPdenovo 软件为例来介绍组装过程。
SOAPdenovo软件的组装过程
(1)通过Kmer之间K-1的overlap关系构建contig(重叠群),如图2:
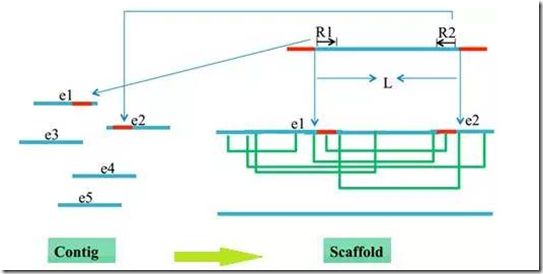
(2)利用pair-end信息,将无overlap关系的contigs搭建成scaffold(脚手架),如图3:
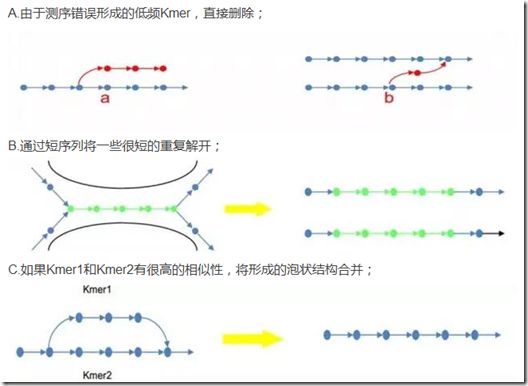
1数据纠错
要得到一个有较高准确性的基因组图谱,首先对测序得到的数据进行处理:
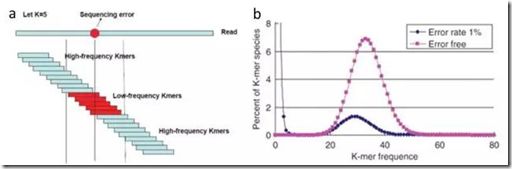
将reads逐bp打断成长度为K的连续核酸序列,如上图a所示,若这条reads中间由于测序错误有一个错误的碱基,那么在得到的Kmer中,也会有一些错误Kmer或者低频Kmer。
绘制Kmer频数分布图时,如上图b所示,Error free代表没有测序错误的Kmer频数分布,Error rate1%代表有1%错误率的Kmer频数分布。
错误Kmer对后续组装会产生很大的困扰,因此,在构建DBG图之前,需要先对数据进行纠错。纠错的两种方法:
(1)基于Read间的比对,通过多序列比对,通过概率模型区分测序错误引起的错误Kmer。这种方法纠错准确,但需要消耗较大的计算资源。如ALLPATH-LG,ECHO等纠错软件都基于这种方法。
(2)通过Kmer频数图谱进行区分,这类软件如SOAPdenovo,Euler等。
2构建Contig
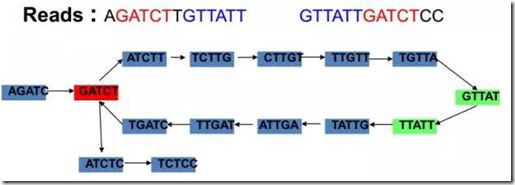
根据Kmer之间的overlap关系进行连接,如下图所示:
reads(read1:AGATCTTGTTATT;read2:GTTATTGATCTCC)逐bp的打断成长度为5bp的Kmer,根据Kmer间的overlap关系进行连接。可以看到两条reads中 GATCT 和 GTTATT 是两个重复的片段,在构建De Bruijn图中,会形成如上图的泡状结构以及多个分支的情况,面对这种很复杂的图,如何才能找到那一条正确的路径呢?
(1)对De Bruijn图进行化简
简化De Bruijn图需要去掉无法继续连接的分支、低覆盖度的分支,并且利用序列信息化简重复序列在De Bruijn图的分叉通路,对于少量的杂合位点,采用随机选择策略,合并杂合位点。通常需要考虑如下几种情况:
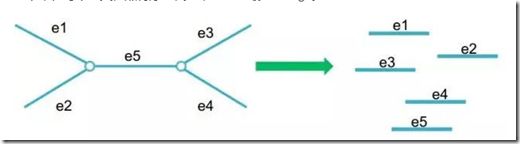
(2)得到一个简化的De Bruijn图后,仍然会因有很多分叉位点无法确定真正的连接关系,因此接下来在每个分叉位点将序列截断,得到了最初contigs。
留给大家一个思考题:根据上述步骤,我们看下图4中复杂的De Bruijn示意图,可以得到什么样的contigs呢?(答案见文末)
3构建scaffold
将测序得到的reads比对回得到的contigs,利用reads之间的连接关系和插入片段大小信息,将contigs组装成scaffolds。
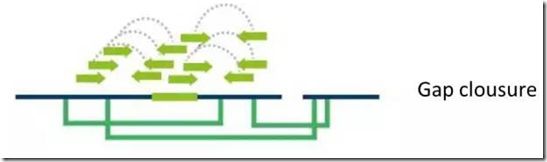
4补洞
得到的scaffold中间会有较多的gap,为了使组装的序列更完整,需再次利用测序的双末端数据之间的配对关系连接contigs,并利用测序数据与已经组装的contig之间的覆盖关系对contig之间空隙进行补洞,延长contigs,补洞后的contigs长度相比补洞之前一般增加2-7倍。
以上就是SOAPdenovo组装的基本过程,看明白了吗?
“揭开组装的神秘面纱下篇”敬请期待~
参考文献
Li RQ, Zhu HM, Ruan J, et al. Denovo assembly of human genomes with massively parallel short readsequencing. Genome Res. 2010, 20(2), 265-72.
Li ZY, Chen YX, Mu DS, et al. Comparison of the two majorclasses of assembly algorithms: overlap-layout-consensus andde-bruijn-graph. Brief Funct Genomics. 2012, 11(1), 25-37
3 string graph算法
有利于组装散列重复序列。
string graph中的节点是长度不一的序列,这些序列是由overlapping reads生成,需要设置一个最小overlap大小。
大部分处理测序数据的软件都是由国外开发的,其中这里提到的SOAPdenovo为华大基因开发的从头拼接软件。
今天就给大家介绍到这里。更多精彩,可见大型免费综合生物信息学资源和工具平台AIPuFu:www.aipufu.com,关注微信公众号:AIPuFuBio。
希望今天的内容对大家有用,会持续更新经典内容,欢迎留言~~!