无重复字符的最长子串
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
首先分析一下题目,求给定字符串的最长不重复子串,思路应该是分治不断降规模,把长度为n的字符串降为n-1的字符串的最长不重复子串,然后到n-2,.... 直到规模为1,关键在于如何得到递推式。
以pwwkew为例做初步分析 ,定义a[i][j]为子串s[i,j]的最长不重复子串,容易得出以下结论:
a[0][0] = len(p) = 1;
a[0][1] = len(pw) = 2;
a[1][2] = len(ww) = 1;
a[i][i] = 1;
字符串s(i,j)包含s(i,j-1)并且只比s(i,j-1)多一个字符s[j],
定义a[i][j] = a[i][j-1] + f(j);
a[i][j] 要么和a[i][j-1]相等,要么比a[i][j-1]多1,
f(j)返回值只能是0或者1,什么时候是1,第一感觉是s(i,j-1)不含字符s(j)的时候。
不过这个感觉是错的,比如pwwk,a[0][2]= len(pww)=2; s(0,2)不含s(3)也就是字符k,a[0][3]= len(pwwk)为2 。
进一步分析,f(j)= 1时,要具备一个条件,也就是s[i,j-1]的最长子串出现的位置必须是紧挨j的位置,
比如pwwk, s(0,2)出现最长子串是pw,而不是ww,a[0][3] != a[0][2] + 1;
再比如pwwke, s(0,3)最长子串是pw或者wk,s(0,4)为wke, a[0][4] = a[0][3] + 1; 因为紧挨s(4)也就是字符e的wk刚好也是s(0,3)的最长子串。
关于计算顺序,先计算单个字符,然后2个字符,然后3个字符,.... n个字符的最长子串。
根据上面分析,code如下
class Solution {
int[][] a;
int n;
public int lengthOfLongestSubstring(String s) {
// a[i,j] 定义为s[i,j]的最长子串的长度
// a[i,j] = a[i,j-1] + s[i,j-1].contain(s[j]) ? 0 :1,
n = s.length();
a = new int[n][n];
for (int i = 0; i < n; i++) {
a[i] = new int[n];
}
int max = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n - i; j++) {
a[j][j + i] = maxLength(s, j, j + i);
if(max < a[j][j + i]){
max = a[j][j + i];
}
}
}
return max;
}
public int maxLength(String s, int i, int j) {
if (i == j)
return 1;
return contain(s, i, j - 1, j) + a[i][j - 1];
}
int max(int a, int b) {
return a > b ? a : b;
}
int contain(String s, int l, int h, int z) {
char ch = s.charAt(z);
int maxLen = a[l][h];
if(a[h-maxLen+1][h] == maxLen){
for (int i = h; i >= h - maxLen+1; i--) {
if (s.charAt(i) == ch) {
return 0;
}
}
return 1;
}
return 0;
}
}
满心欢喜,折腾了半天终于完工了,拿来测试用例也都OK,平台提交一下.....超出内存限制(98/100),通过了97个用例,第98是一个几页纸长的一个字符串。
代码使用了n*n的int数组保存中间计算结果(n为字符串长度),当n非常大的时候.....
好吧,想办法减一点内存消耗。
其实二维数组有将近一半没有使用,真正用到的只有矩阵A[i,j]的(j>i部分)的半个矩阵
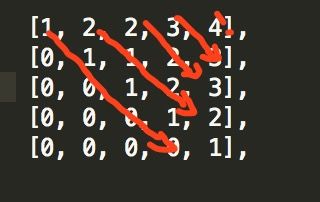
如pwwke的计算过程和结果如下,箭头表示计算过程,从长到短。
矩阵的左下全都没用,这个应该算是稀疏矩阵吧,大学时期学好像有听过稀疏矩阵的压缩存储,不管了,很遥远了,尝试用一维数组来存储这矩阵,数组的长度为 n + (n-1) + ... + 1 = n*(n+1)/2 ,比 n ^2还是省很多了。
接下来就是坐标换算了, 二维的坐标换到一维
(i,j )---> index
求index(i,j)的表达式。
对照上面的图 (i为行数,j为列数)
index(i,j) = index(i,i) + j-i; // 先定位到第i行对角线位置,再偏移j-i
index(i, i)= n + (n-1) +...(n-i+1) = (2n-i+1) /2
index(i, j) = (2n-i+1) /2 + j-i
合并一下
index(i, j) = i*(2n-1-i)/2 + j
i = 0 时也满足。
好了,修改代码,把算法中的二维数组变成一维,修改后代码如下
int[] a;
int n;
int twoN_1; // 2n-1
public int lengthOfLongestSubstring(String s) {
// a[i,j] 定义为s[i,j]的最长子串的长度
// a[i,j] = a[i,j-1] + s[i,j-1].contain(s[j]) ? 0 :1,
n = s.length();
twoN_1 = 2*n -1;
a = new int[n*(n+1)/2];
// j ---->
// i 00 01 02 03 04
// | 10 11 12 13 14
// ! 20 21 22 23 24
// ! 30 31 32 33 34
// 40 41 42 43 44
// a[b][c] --> a[index];
// index = i*(2n-1-i)/2 + j
int max = 0;
int tmpIndex = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n - i; j++) {
tmpIndex = index(j,j+i);
a[tmpIndex] = maxLength(s, j, j + i);
if(max < a[tmpIndex]){
max = a[tmpIndex];
}
}
}
return max;
}
public int index(int i,int j){
return i * (twoN_1 -i) /2 +j;
}
public int maxLength(String s, int i, int j) {
if (i == j)
return 1;
return contain(s, i, j - 1, j) + a[index(i,j-1)];
}
int max(int a, int b) {
return a > b ? a : b;
}
int contain(String s, int l, int h, int z) {
char ch = s.charAt(z);
int maxLen = a[index(l,h)];
if(a[index(h-maxLen+1,h)] == maxLen){
for (int i = h; i >= h - maxLen+1; i--) {
if (s.charAt(i) == ch) {
return 0;
}
}
return 1;
}
return 0;
}
这下应该行了吧,......... 生活总是残酷的,很多时候,努力了也不一定会有好的结果,还是超出内存限制。
看来得换另外的方式了,二维数组内存消耗太大了,尽管改成了一维,但本质上还是二维,那就来个真正的一维吧。
一顿分析猛如虎......
定义a[j]为 s(0,j)的最长子串, 真一维了,a[n-1] 为题目所求。
a[j] 与 a[j-1]的递推式跟上面一致,关键也是s(0,j-1)的最长子串是以j-1结尾的
s(0,j-1) 的最长子串长度为 max,如果s(j-max, j-1)这段长度为max的子串是s(0,j-1)的最长子串,即s(j-max, j-1)没有重复字符,而且如果s(j-max, j-1)不含字符s(j),则s(j-max, j) 是 s(0,j)的最长子串
那关键问题就是要判断s(j-max, j-1) 这一小段有没有重复了,s(j-max, j-1)有没有包含字符s[j]了,这个好说,弄一个HashSet来协助判断。
通过上面分析,形成新的代码如下
int []a;// a[i] 标示 s[0,i]的最大不重复子串长度
int n;
public int lengthOfLongestSubstring(String s) {
n = s.length();
a = new int[n];
if(n == 0) return 0;
a[0] = 1;
for(int i=1;i hs = new HashSet();
// pwwk e 1 2 2 2
int fun(String s,int i){ // 返回0 || 1
int h = i-1;
int maxLen = a[h];
char tmp;
hs.clear();
for(int j=h-maxLen+1 ;j<=h;j++){
tmp = s.charAt(j);
if(hs.contains(tmp))
return 0;
else hs.add(tmp);
}
return hs.contains(s.charAt(i)) ? 0 : 1;
}
这次提交通过了。
以上是笔者对这道理整个思考和解答过程,权且记录。