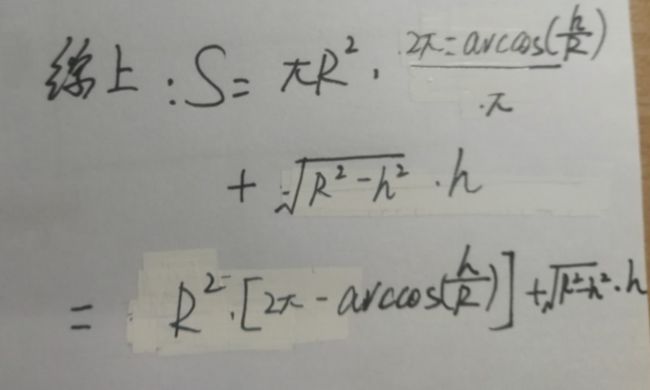前言
近日拜读了Daniel Shiffman先生的著作——《代码本色:用编程模拟自然系统》,决定做一组习作,来对书中提到的随机行为及牛顿运动学进行理解,并对一些实例进行拓展学习,从而提升自己相关方面的知识水平和实践能力。
《代码本色》第2章概述
在第2章中,作者向我们介绍了牛顿的力学三大定律。分别为:
牛顿第一运动定律:除非有不均衡外力的作用,否则物体始终保持静止或匀速直线运动状态。
牛顿第二运动定律:力等于质量乘以加速度。
牛顿第三运动定律:每个作用力都有一个大小相等、方向相反的反作用力。
随后,作者通过实例告诉我们如何在Processing里模拟力,这里包括了制造质量,制造各种外力,如引力,摩擦力,空气阻力和流体阻力等等。
在这一章中,我印象比较深的点是各种力的代码模拟,通过面向对象的思想,将力的表现用代码实现。下面,我将介绍我根据本章内容而创作的Processing编程习作。
习作
创作过程
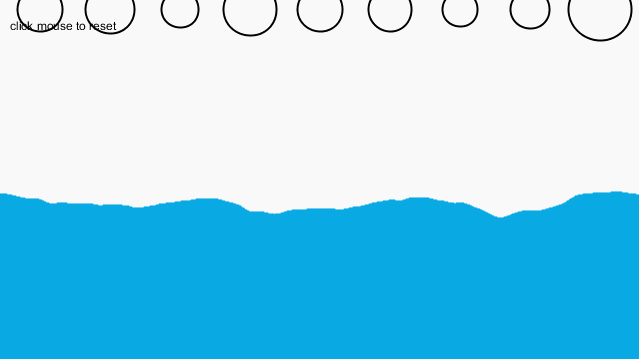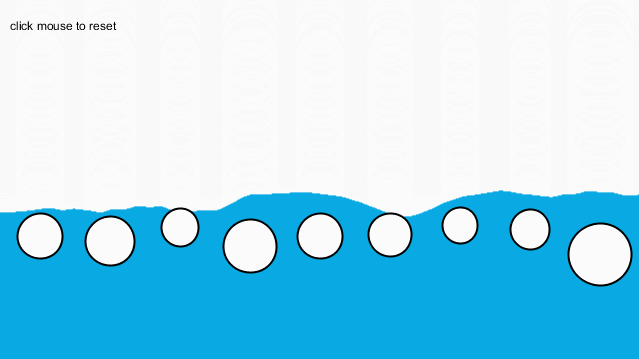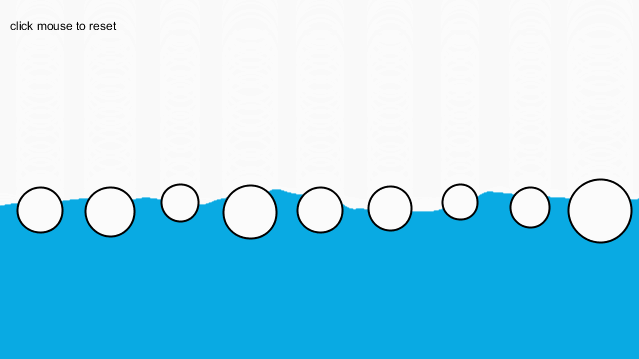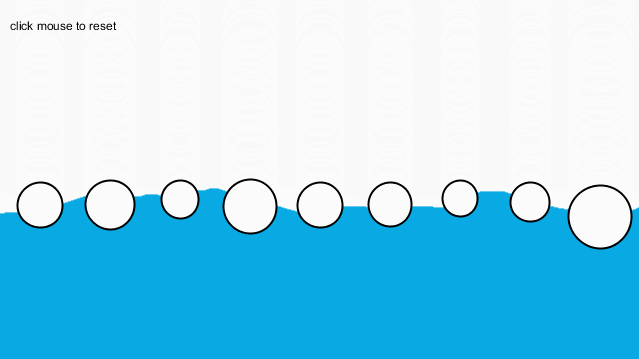
对于浮力的模拟,其实说起来容易做起来难。首先,我利用了书中的一个例子,即2-5,该例子中已经实现了重力和流体阻力。书中定义了一个新的类型——Liquid,并在物体进入液体时给他一个drag的力,此外,阻力的大小等于阻力系数乘以对象速度的平方,且方向与Mover对象的速度方向相反。这样一来就定义了这个阻力,实现了流体阻力的效果。
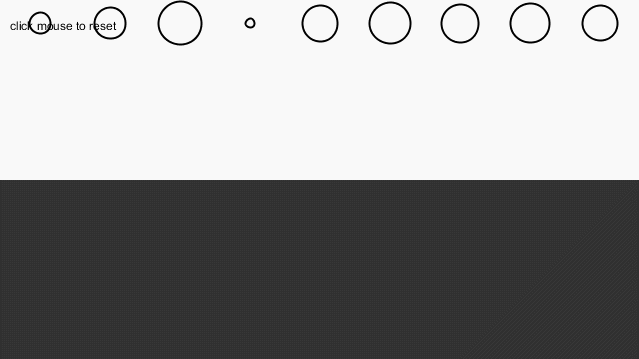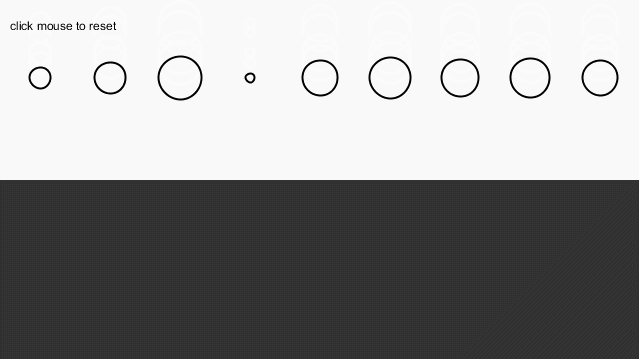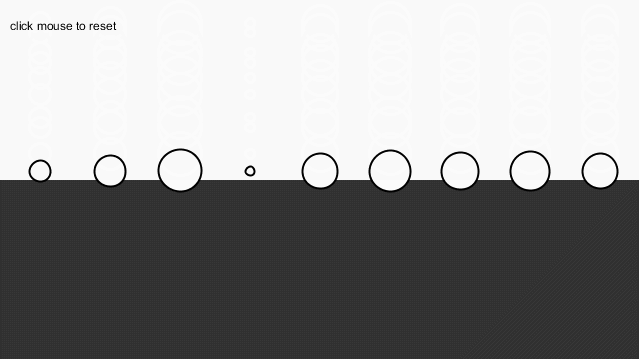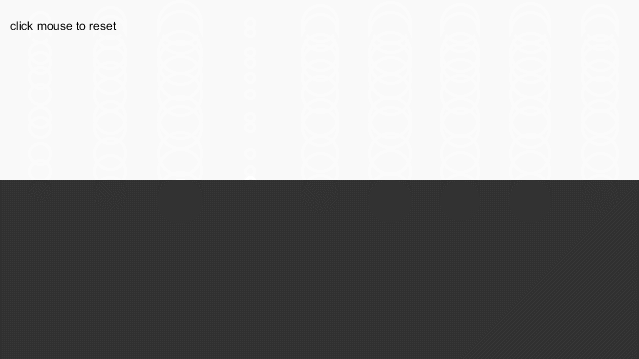
首先,我们来看一下没有浮力的情况:
而我要做的是在这个基础上在Liquid类中添加浮力的效果,首先,我们来复习一下初中物理的知识——浮力计算公式。
公式1. F浮=F向上-F向下
“F向上”指下表面受到的向上的力,F向下指上表面受到的向下的力,这是浮力的最原始的计算公式。
公式2. F浮=G排=ρ液gV排
这是根据阿基米德原理得到的,V排指排出液体的体积,ρ液指液体密度。
公式3. F浮=G物
即ρ液gV物,利用二力平衡,即根据漂浮、悬浮的物体浮力与自重相等。
公式4. F浮=G物-F拉
测量浮力时根据此公式计算,F拉指的是弹簧测力计的拉力。
公式5. F浮=ρgh
h指的是物体全部浸入液体中时表面距离液面的高度。
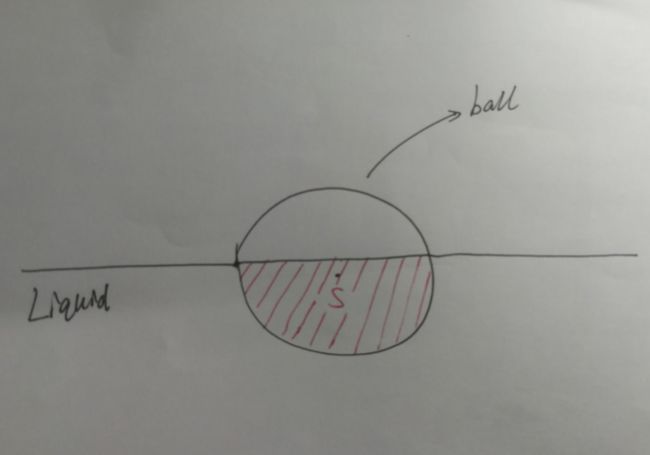
我们比较常用的是公式2。浮力是什么时候开始起作用的呢?答案是当物体接触到液体表面的那一刻开始。根据公式2,物体浸入液体的面积(其实应该是体积,在二维中称之为面积)就是我们说的V排。
对此,我画了个草图帮助理解:
那么,我们在程序中容易得到的值是球心的坐标和液体表面的高度(即y坐标),那么我们该如何计算S的面积呢?
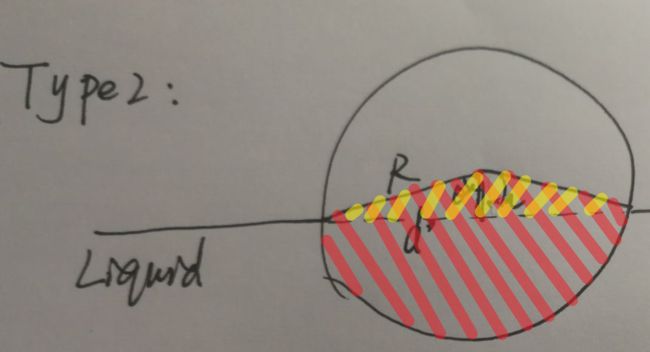
我分了两种情况,分别画了图帮助理解:
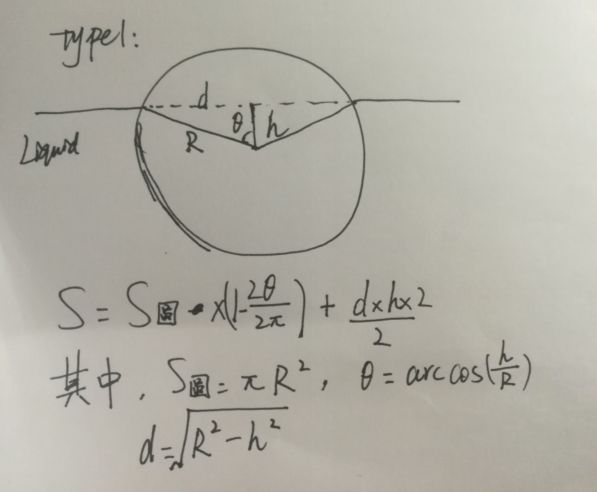
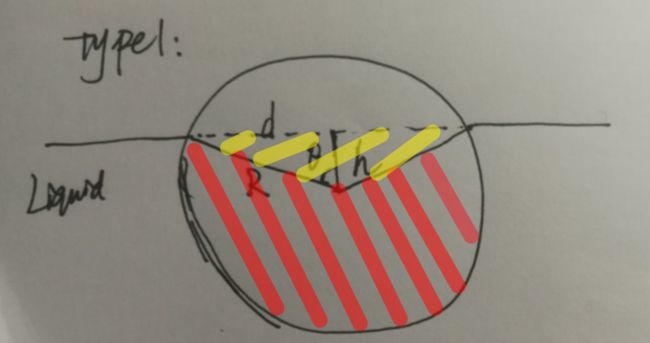
情况1:
这种情况是圆心坐标已经低于水平面了,换言之,就是一半以上的圆已经进入了液体。我们假设:
R为圆的半径
h为水面高度-圆心的高度
那么S这一块的面积就是红色的扇形面积加上黄色的这个等腰三角形的面积。
其中,扇形的面积又可以通过图中标出的θ角来求出,公式为(1-2θ/2π)×S圆。
三角形的面积可以根据勾股定理算出d,面积为dh2/2。
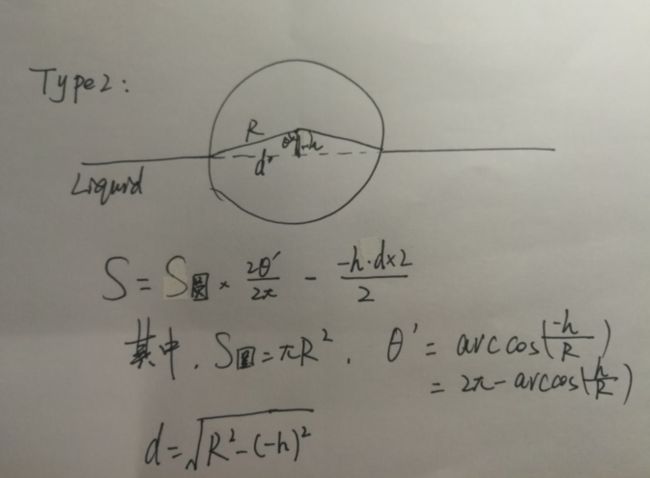
情况2
接下来,我们来看第二种情况。这种情况是圆心坐标高于水平面了,换言之,进入液体的面积不到一半。
需要注意的是,这里的h应该是-h,原因是圆心还没有过液体表面,所以这一段距离为-h。其他的计算方式和情况1相似。唯一不同的是,此时的面积S为扇形面积-三角形面积:
这时,我在进行公式推导时发现了一个问题,根据arccos()函数的性质,arccos(-x)=2π-arccos(x)。运用在这个问题中,就是arccos(h/R)=2π-arccos(-h/R)。而这个2π又刚好让扇形面积的正反两面抵消。经过化简,我们可以将两个公式合并成同一个。公式如下:
至此,V排的公式就已经得出,接下来就可以编写代码了:
首先,在Liquid类中,我添加了一个获取浮力的方法:
PVector buoyancy (Mover m)
{//浮力
PVector l = m. position;
float h=y-l. y;//水面高度和球心高度的差
float R=m. mass*16/2;//半径
float Sf= (R*R) * (2*PI-acos (h/R)) +sqrt (R*R-h*h) *h;//V排
PVector buoyancyForce;
buoyancyForce=new PVector (0, -0.1*Sf, 0);
buoyancyForce.mult(0.001);//由于整个程序中的力都比较小,浮力也不能太大
return buoyancyForce;
}
接着,在主程序中,将这个力应用。
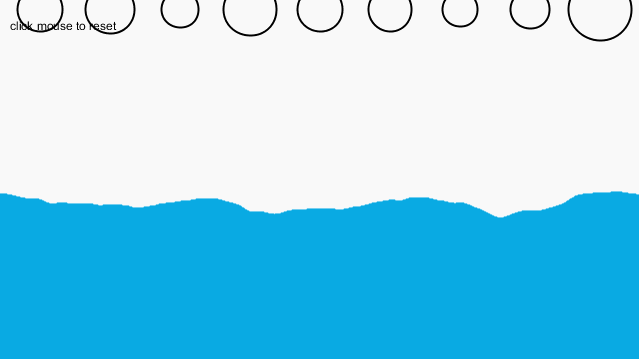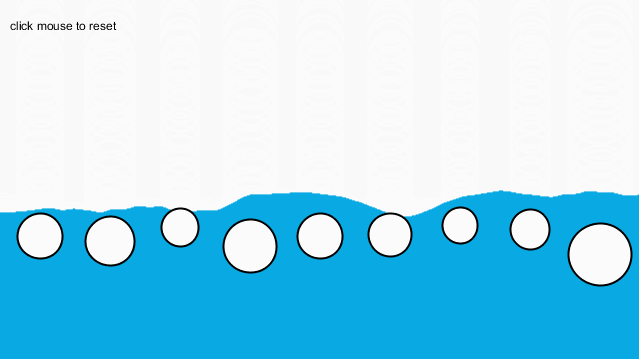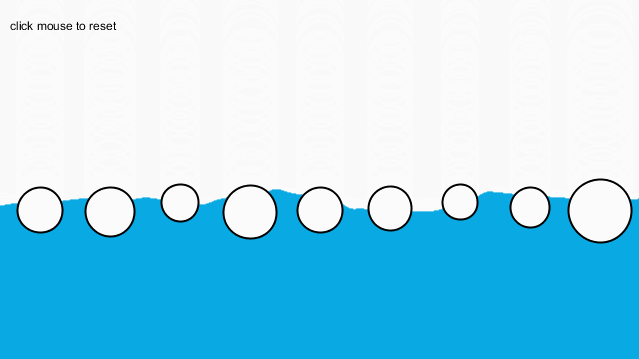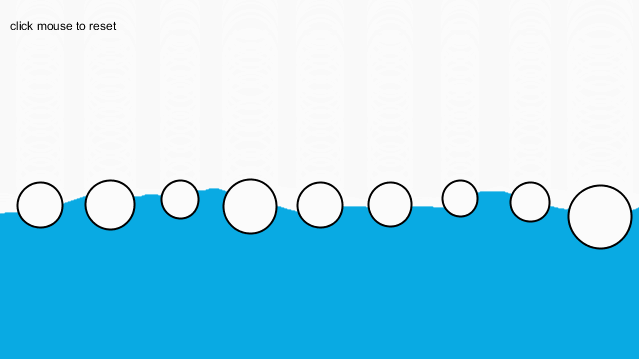
if(liquid.y-movers[i].position.y运行结果如下:
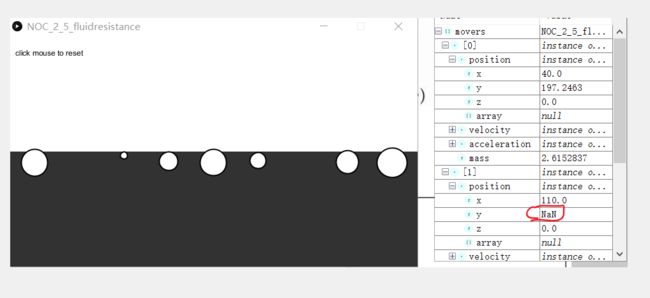
为什么球突然消失了呢,这使我非常困惑。我检查了很久,也没有发现问题在哪里。最后我利用processing的调试器,进行逐步调试并仔细观察变量变化,终于发现了问题所在:
可以看到,消失的小球的y变成了NaN。
我去查阅了资料,发现会出现NaN的最常见情况就是用把0作为了除数,或者是其他的计算错误。我开始认真分析我的代码中哪里会出现这种错误。最后,锁定了一个嫌疑人——acos()函数,也就是arccos函数。
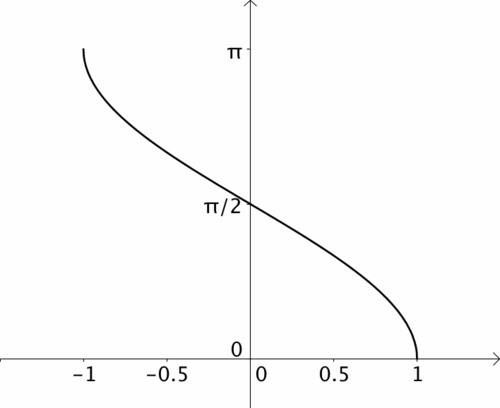
我发现在h进行变化的时候,会无限接近于R,也就是球体逐渐整个进入液体的过程。而arccos的函数图像是这样的:
也就是说,arccos(1)和arccos(-1)的结果是无穷。而h/R的值是会到达这个取值范围的!
所以我做了个判断,如果h的绝对值逼近R了,这种情况也就是整个球就快要全部浸入了,这是,我更换浮力的计算公式。代码如下:
PVector buoyancy (Mover m)
{//浮力
PVector l = m. position;
float h=y-l. y;//水面高度和球心高度的差
float R=m. mass*16/2;//半径
float Sf= (R*R/2) * (2*PI-acos (h/R)) +sqrt (R*R-h*h) *h;//V排
PVector buoyancyForce;
if(-h-R<0)
{
buoyancyForce=new PVector (0, -0.1*Sf, 0);
buoyancyForce.mult(0.001);//由于整个程序中的力都比较小,浮力也不能太大
println(buoyancyForce);
}
else
{
buoyancyForce=new PVector(0,-density *m.mass,0);
}
return buoyancyForce;
}
其中density为液体的密度。
这样一来,就可以保证不会触碰到这个“危险地带”。最终效果如下:
最后,我又根据第0章的知识,使用了Perlin噪声,模拟了海面的效果:
Perlin噪声的这段代码如下:
void display() {
stroke(#09AAE3);
fill(50);
//rect(x, y, w, h);
float x = 0;
while (x < width) {
line(x, 180 + 50 * noise(x / 100, t), x, height);
x = x + 1;
}
t = t + 0.01;
}
最后,贴出全部代码:
Mover类:
class Mover {
// position, velocity, and acceleration
PVector position;
PVector velocity;
PVector acceleration;
// Mass is tied to size
float mass;
Mover(float m, float x, float y) {
mass = m;
position = new PVector(x, y);
velocity = new PVector(0, 0);
acceleration = new PVector(0, 0);
}
// Newton's 2nd law: F = M * A
// or A = F / M
void applyForce(PVector force) {
// Divide by mass
PVector f = PVector.div(force, mass);
// Accumulate all forces in acceleration
acceleration.add(f);
}
void update() {
// Velocity changes according to acceleration
velocity.add(acceleration);
// position changes by velocity
position.add(velocity);
// We must clear acceleration each frame
acceleration.mult(0);
}
// Draw Mover
void display() {
stroke(0);
strokeWeight(2);
fill(255);
ellipse(position.x, position.y, mass*16, mass*16);
}
// Bounce off bottom of window
void checkEdges() {
if (position.y > height) {
velocity.y *= -0.9; // A little dampening when hitting the bottom
position.y = height;
}
}
}
Liquid类:
// Liquid class
class Liquid {
float t=0;
// Liquid is a rectangle
float x, y, w, h;
// Coefficient of drag
float c;
float density;
Liquid(float x_, float y_, float w_, float h_, float c_,float density_) {
x = x_;
y = y_;
w = w_;
h = h_;
c = c_;
density=density_;
}
// Is the Mover in the Liquid?
boolean contains(Mover m) {
PVector l = m.position;
return l.x > x && l.x < x + w && l.y > y && l.y < y + h;
}
// Calculate drag force
PVector drag(Mover m) {
// Magnitude is coefficient * speed squared
float speed = m.velocity.mag();
float dragMagnitude = c * speed * speed;
// Direction is inverse of velocity
PVector dragForce = m.velocity.get();
dragForce.mult(-1);
// Scale according to magnitude
// dragForce.setMag(dragMagnitude);
dragForce.normalize();
dragForce.mult(dragMagnitude);
return dragForce;
}
PVector buoyancy (Mover m)
{//浮力
PVector l = m. position;
float h=y-l. y;//水面高度和球心高度的差
float R=m. mass*16/2;//半径
float Sf= (R*R/2) * (2*PI-acos (h/R)) +sqrt (R*R-h*h) *h;//V排
PVector buoyancyForce;
if(-h-R<0)
{
buoyancyForce=new PVector (0, -0.1*Sf, 0);
buoyancyForce.mult(0.001);//由于整个程序中的力都比较小,浮力也不能太大
println(buoyancyForce);
}
else
{
buoyancyForce=new PVector(0,-density *m.mass,0);
}
return buoyancyForce;
}
void display() {
stroke(#09AAE3);
fill(50);
//rect(x, y, w, h);
float x = 0;
while (x < width) {
line(x, 180 + 50 * noise(x / 100, t), x, height);
x = x + 1;
}
t = t + 0.01;
}
}
主程序类:
Mover[] movers = new Mover[9];
// Liquid
Liquid liquid;
void setup() {
size(640, 360);
reset();
// Create liquid object
liquid = new Liquid(0, height/2, width, height/2, 0.1,0.12);
}
void draw() {
background(255);
// Draw water
liquid.display();
for (int i = 0; i < movers.length; i++) {
// Is the Mover in the liquid?
if (liquid.contains(movers[i])) {
// Calculate drag force
PVector dragForce = liquid.drag(movers[i]);
// Apply drag force to Mover
movers[i].applyForce(dragForce);
}
// Gravity is scaled by mass here!
PVector gravity = new PVector(0, 0.1*movers[i].mass);
// Apply gravity
movers[i].applyForce(gravity);
if(liquid.y-movers[i].position.y总结
本文介绍了《代码本色:用编程模拟自然系统》第2章的主要内容,并在示例的基础上进行了拓展性的创作,创作了流体阻力重力和浮力的模型。