教你用堆排序解决topk问题

教你用堆排序解决topk问题，同时学会堆排序。

1、什么是Top K问题？

找到数组中最大（最小）的K个数，例如7,6,3,5,2，Top3 的意思就是 找出最小的三个数即为：3,5,2。

• 方法1：对数组全部排序，然后根据要求取其中K个数
• 方法2：只对K个排序，例如冒泡是一个很常见的排序方法，每冒一个泡，找出最大值，冒k个泡，就得到TopK。
• 方法3：就是本文主要要讲的堆，构建一个大顶堆(小顶堆)，然后堆顶就是最大值（最小值）取出最大值后调整堆，再继续取堆顶值，取到k为止。

看完了topk的问题，我们现在看看怎么用堆来解决这个问题。首先让我们一起来看看堆是一种什么样的数据结构。

2、什么是堆？

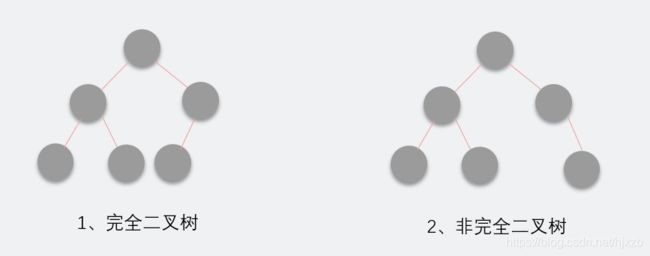
• a、它是完全二叉树，除了树的最后一层节点不需要是满的，其它的每一层从左到右都是满的。注意下面两种情况，第二种最后一层从左到右中间有断隔，那么也是不完全二叉树。
  

• b、堆中的每一个节点的关键字都大于（或等于）这个节点的子节点的关键字。

3、怎么用完全二叉树表示数组？

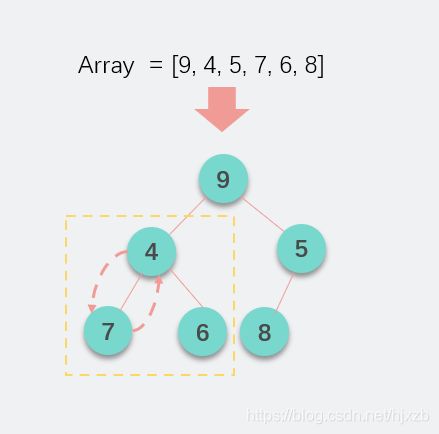
那好，如果给你定你一个数组：[9, 4, 5, 7, 6, 8] 转换成完全二叉树。那么转换后的结构如下图所示：

那我们可以看到这个完全二叉树不满足前面堆的定义：每一个节点的关键字都大于（或等于）这个节点的子节点的关键字。也就是父节点要大于子节点。这种用数组实现的二叉树，假设节点在数组中的索引值为index，那么：

• 节点的左子节点是 2*index+1，

• 节点的右子节点是 2*index+2，

• 节点的父节点是 （index-1）/2。

例如数组中的4，它在数组中的index为1。左子节点7的index值为3=2x1+1，右子节点6的index值为4=2x1+2。上图中的完全二叉树不是堆结构，那么我们要怎么对它调整变成堆呢？下面就看一下怎么调整完全二叉树变成堆。

4、怎么使完全二叉树变成堆？

我们假设上图中的4进行调整，因为4没有它的子节点值大。如下图所示：

我需要将4和7的位置进行一个互换，才能满足堆的性质。交换之后如果说4就变成了7.如果7的父节点比7小就要再次调整，本例子中由于由于不比父节点大，所以不用再次调整。那如果我们将这个操作封装成一个函数要怎么操作呢?

func AdjustHeap(array []int, length, i int) {
	//调整第i个元素
	if i > length {//终止条件
		return
	}
	max := i
	c1 := 2*i + 1 //左子节点index值
	c2 := 2*i + 2 //右子节点index值
    //和两个子节点进行比较，取3个当中的最大值所在的index值
	if c1 < length && array[max] < array[c1] {
		max = c1
	}
	if c2 < length && array[max] < array[c2] {
		max = c2
	}
	if max != i {//父节点不是最大，就要和其中的一个子节点进行交换
		array[i], array[max] = array[max], array[i]
		AdjustHeap(tree, length, max) //对交换后的那个元素再次调整，因为可能使得上一层或者下一层不满足堆的性质
	}
}

5、怎么构造堆？

从第一个非叶子结点从下至上，从右至左调整结构。本题第一个非叶子节点也就是4，第二个是5。那么第一个非叶子节点它的index值是多少呢？

index = (length-1)/2 - 1

只需要将这个index 递减至0的进行一次循环调用调整堆的函数，就最终将一个完全二叉树变成了一个大顶堆的结构。

 //从第一个非叶子结点从下至上，从右至左调整结构
 func BuildHeap(tree []int, length int) {
	for i := (length-1)/2 - 1; i >= 0; i-- {
		AdjustHeap(tree, length, i)
	}
}

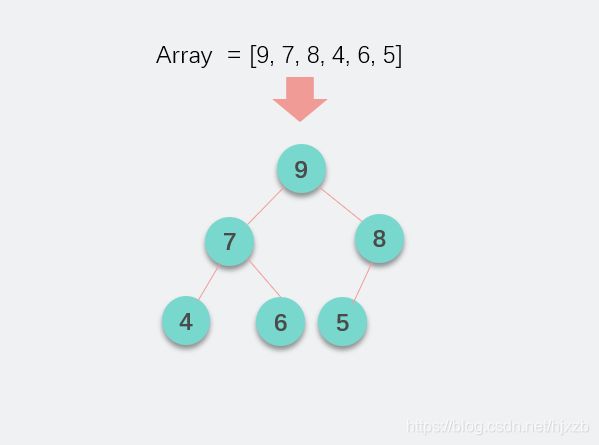
本例题中调整完之后变成下图所示的结果。

注意数组中的数字变化，此时仍然没有满足有序。但是第一个数变成了最大值，也就是我们所说的大顶堆。

6、利用大顶堆排序

堆排序只需要来一个倒序遍历，每次将第一个元素移到最后就可以了。交换的同时，重新调整大顶堆。

func HeapSort(array []int) {
	BuildHeap(array, len(array)) //构造大顶堆
	for i := len(array) - 1; i >= 0; i-- {
		array[i], array[0] = array[0], array[i] //将最大值和最后一个元素互换，最后一个元素就变成了最大值
		AdjustHeap(array, i, 0) //第一个元素已经变化，需要重新调整使之重新变为大顶堆        
	}
}

那么如果是topk的问题，只需要循环k次即可，后面K个元素就是有序的了。

7、例题巩固

给定String类型的数组strArr，再给定整数k，请严格按照排名顺序打印 出次数前k名的字符串。

[要求]

如果strArr长度为N，时间复杂度请达到O(N \log K)O(NlogK)

输出K行，每行有一个字符串和一个整数（字符串表示）。
你需要按照出现出现次数由大到小输出，若出现次数相同时字符串字典序较小的优先输出

示例 输入

["1","2","3","4"],2

样例返回值

[["1","1"],["2","1"]]

参考答案：

func topKstrings(strings []string, k int) [][]string {
	// write code here
	result := [][]string{}
	//统计频次
	resMap := map[string]int{}
	for _, v := range strings {
		resMap[v]++
	}
	length := len(strings)

	//构建堆
	for i := (length-1)/2 - 1; i >= 0; i-- {
		AdjustHeap(resMap, strings, length, i)
	}
	fmt.Print(strings)

	//输出结果
	for i := length - 1; i >= 0; i-- {
		strings[i], strings[0] = strings[0], strings[i]
		//保存结果
		t := []string{strings[i]}
		feq := strconv.Itoa(resMap[strings[i]])
		t = append(t, feq)
		result = append(result, t)
		if len(result) >= k {
			return result
		}
		AdjustHeap(resMap, strings, i, 0)
	}
	return result
}

func AdjustHeap(resMap map[string]int, result []string, length, i int) {
	if i > length {
		return
	}
	max := i
	c1 := 2*i + 1
	c2 := 2*i + 2
	if c1 < length {
		if resMap[result[c1]] > resMap[result[max]] {
			max = c1
		} else if resMap[result[c1]] == resMap[result[max]] && result[c1] < result[max] {
			max = c1
		}
	}
	if c2 < length {
		if resMap[result[c2]] > resMap[result[max]] {
			max = c2
		} else if resMap[result[c2]] == resMap[result[max]] && result[c2] < result[max] {
			max = c2
		}
	}
	if max != i {
		result[i], result[max] = result[max], result[i]
		AdjustHeap(resMap, result, length, max)
	}
}

参考资料：

1、https://www.bilibili.com/video/BV1Eb41147dK?t=1568

2、https://www.nowcoder.com/practice/fd711bdfa0e840b381d7e1b82183b3ee?tpId=117&&tqId=35559&rp=1&ru=/ta/job-code-high&qru=/ta/job-code-high/question-ranking