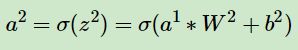卷积神经网络(CNN)结构详解
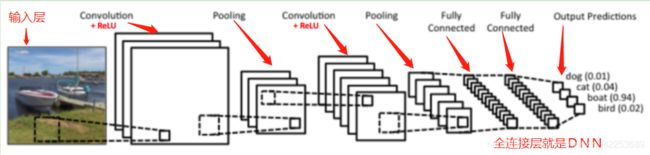
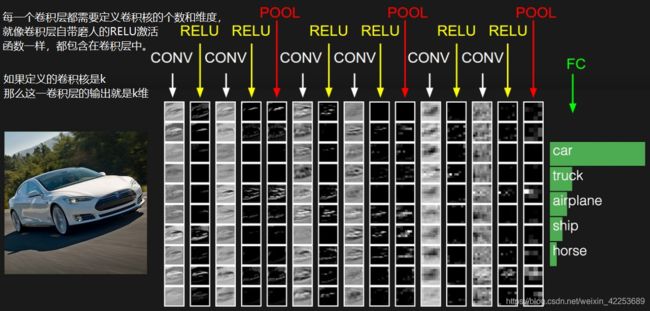
一、CNN的基本结构:
1.图像就是输入层
2.接着是CNN特有的卷积层(convolution),卷积层的自带激活函数使用的是ReLU
3.接着是CNN特有的池化层(pooling),
4.卷积层+池化层的组合可以在隐藏层中出现很多次。也可以灵活组合,卷积+卷积+池化、卷积+卷积等
5.在若干卷积层+池化层之后是全连接层(fully connected layer),其实就是DNN结构,只是输出层使用了Softmax激活函数来做图像识别的分类
6.一般fc就为CNN的全连接层。全连接层一般包括最后用softmax激活函数的输出层
二、卷积的原理:
https://mp.csdn.net/editor/html/109519709
总结:一补二乘三遍历,CNN中采用的是valid模式
三、多维卷积,
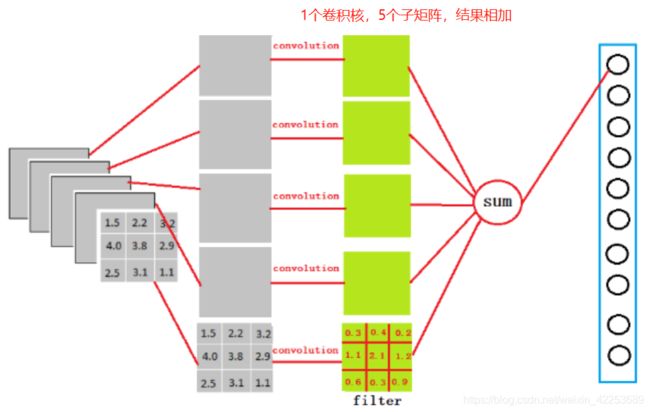
如有三个5*5的矩阵,三个2*2的卷积核,也就是被卷机矩阵是5*5*3的tensor,卷积核是2*2*3的tensor。或者输入是RGB图像,可以分成三层。那么在卷积的时候,就是将三个二维的tensor进行卷积之后结果相加再加上偏置。
参考动图https://cs231n.github.io/assets/conv-demo/index.html
注意 一排下来是一个卷积核,只不过这个卷积核的tensor.size()是n x n x 3。对应的偏置也是3维的tensor
四、CNN中特有的池化层
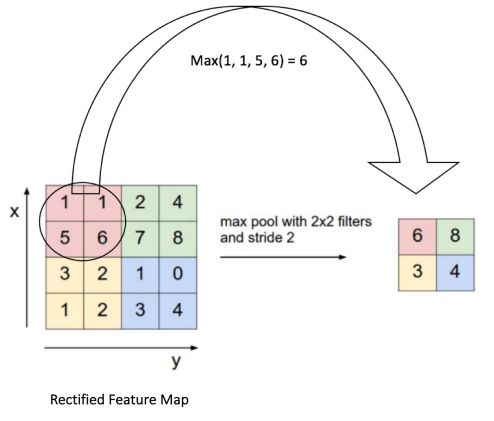
池化,就是将输入张量的各个子矩阵进行维度压缩。有max和average两种方式。
filter的维度为nxn,那么就用该filter在输入张量上扫过,每一个重叠小块的最大值或平均值作为输出。就实现将n维变到1维。
## CNN的输入:
如果是2维张量,就是有一个2维矩阵n x n。
如果是3维张量,就是有m个2维矩阵 n x n x m。m不一定是3。
如果是4维张量,就是有k个3维矩阵,每一个三维矩阵又是m个二维矩阵。所以四维输入的矩阵形式其实是 n x n x m x k。 k也不一定是4.
CNN的全连接层
经过卷积层和池化层,输入层被输出成了一堆二维的tensor。
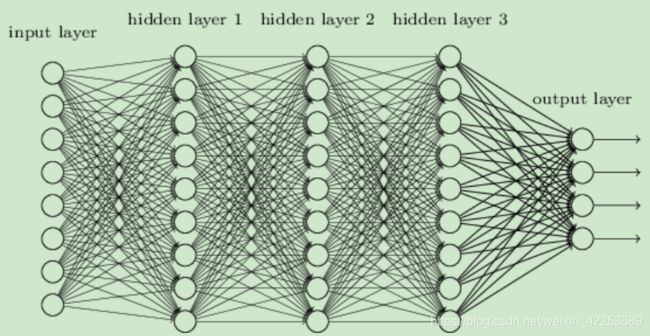
全连接层的每一层都是有许多神经元的平铺。基本结构如下图
那么如何将前面输出的tensor转换到1xn的形式呢。n为第一层全连接层的神经元个数。
此文 讲:
类似于做卷积。在这里卷积核的 kernel_size = 3x3x5。也就是用5个3x3的子矩阵 对卷积池化层的输出结果 进行卷积。每一个卷积核卷积之后的结果就是一个神经元的输入。所以要将这5个子矩阵对应到4069个神经元的第一层全连接层,就是用维度为3x3x5x4069的卷积核进行卷积。
这里作用有两个:
1.做卷积,将卷积池化层的输出对应到全连接层。
2.把分布式特征representation映射到样本标记空间,输出为一个值,根据这个值判断分类结果。大大减少特征位置对分类带来的影响
3.多个全连接层,能够有效解决非线性问题
# 全连接层一般会进行dropout正则化。这里有个特点,对批训练的第一批数据训练师,随机失活一些神经元,得到的残缺DNN结构对数据进行训练,并更新整个网络的所有神经元的w和b参数。
训练后,失活的神经元复活。下一批数据来的时候,又随机失活一部分神经元得到一个新的残缺DNN结构,这两次得到的结构并不一定相同。
CNN前向传播算法
一、CNN输入层前向传播到卷积层
1.卷积核的维度(子矩阵的个数)和输入tensor的子矩阵个数是一致的。
上标是第几层,a是该层的输入,w是该层的权重矩阵,b是该层的偏置。z是该层输入的中间输出,δ是激活函数,❉表示卷积。
2.卷积核的个数和维度需要在卷积层中定义,是卷积层的一个属性。就像卷积层自带的relu
激活函数一样。
3.卷积核的个数一般不止一个,比如是k,那么该卷积层的输出或者下一层卷积层的输入就是k个。
4.填充padding(p),为了更好的识别边缘,一般在输入矩阵周围添加几层0。层数取决于卷积核的维度。
5.步幅stride。
二、隐藏层前向传播到卷积层。
前面所有的卷积层和池化层包括全连接层组成的就是隐藏层。
这里的输入是隐藏层来的。
也需要定义CNN模型的卷积核的个数,卷积核子矩阵的维度,填充大小,及步幅。
三、隐藏层前向传播到池化层:
1.定义池化趋于的大小k
2.池化的标准,max或者average
3.若输入是nxn ,输出的维度就是n/k
四、隐藏层前向传播到全连接层
1.激活函数的选择rule、sigmoid、tanh、softmax
2.经过若干全连接层(一般不止一层),最后一层就是输出层。输出层一般选softmax做激活函数。其他的一般选另外的激活函数。
3.要定义全连接层各层的神经元
五、总结
1.输入是一个图片样本。CNN模型的层数,所有隐藏层的参数和类型
2.若为卷积层,给出卷积核的个数、维度、填充、步幅
若为池化层,给出池化区域的大小k和池化标准
对于全连接层,给出各层的神经元数和激活函数的类型
3.根据填充,得到输入的张量a^1.并初始化所有隐藏层的参数w和b
4.for l in range(2,L):
最后补充一句:卷积层和全连接层表达式看似相同,实际有很大的区别:
在卷积层中W是卷积核,星号(*)表示卷积,W卷积核矩阵是右乘的。W是却别与被卷机矩阵a的矩阵。
在全连接层中,W是参数矩阵,b是偏置,是单纯的矩阵的乘法而不是卷积,且是左乘。W和b 都是该层神经网络附带的属性只不过在训练过程中要不断跳整。
参考:CNN 入门讲解:什么是全连接层(Fully Connected Layer)?
深度神经网络(DNN)的正则化
卷积神经网络(CNN)模型结构
卷积神经网络(CNN)前向传播算法