部分卷积网络结构(一)
文章目录
- 前言
- 一、LeNet
-
- 1.1 网络结构与亮点
- 1.2 代码
- 二、AlexNet
-
- 2.1 网络结构与亮点
- 2.2 代码
- 三、VGG
-
- 3.1 网络结构与亮点
- 3.2 代码
- 四、GoogLeNet
-
- 4.1 网络结构与亮点
- 4.2 代码
- 五、ResNet
-
- 5.1 网络结构与亮点
- 5.2 代码
- 六、MobileNet
-
- 6.1 网络结构与亮点
- 6.2 代码
前言
本文主要记录了一些经典的卷积网络架构,以及相应的pytorch代码。
提示:以下是本篇文章正文内容。
一、LeNet
1.1 网络结构与亮点
网络结构:
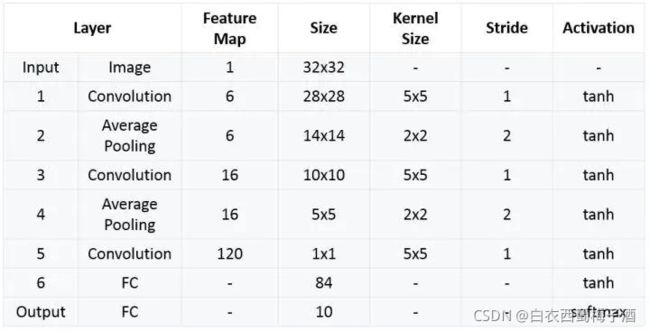
亮点:
1)卷积神经网络使用三个层作为一个系列: 卷积,池化,非线性
2)使用卷积提取空间特征
3)使用映射到空间均值下采样(subsample)
4)双曲线(tanh)或S型(sigmoid)形式的非线性
6)层与层之间的稀疏连接矩阵避免大的计算成本
1.2 代码
import torch
import torch.nn.functional as F
import torch.nn as nn
import torch.optim as optim
import torchvision
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image ##用该库来打开图片导入对应的数据
## 显示图片
def imshow(img):
npimg=img.numpy()
plt.imshow(np.transpose(npimg,(1,2,0))) ## 将图片的维度转换
plt.show()
class LeNet(nn.Module):
def __init__(self):
super(LeNet,self).__init__()
self.conv1=torch.nn.Conv2d(3,16,(5,5))
self.pool1=torch.nn.MaxPool2d(2,2) ## 不指定步长,则默认为kersize
self.conv2=torch.nn.Conv2d(16,32,(5,5))
self.pool2=torch.nn.MaxPool2d(2,2)
self.fc1=torch.nn.Linear(32*5*5,120)
self.fc2=torch.nn.Linear(120,84)
self.fc3=torch.nn.Linear(84,10)
def forward(self,X):
X=F.relu(self.conv1(X))
X=self.pool1(X)
X=F.relu(self.conv2(X))
X=self.pool2(X)
X=X.view(-1,32*5*5)
X=F.relu(self.fc1(X))
X=F.relu(self.fc2(X))
Z=self.fc3(X)
return Z
x_test=0
net=LeNet()
loss_func=torch.nn.CrossEntropyLoss()
optimizer=torch.optim.Adam(net.parameters(),lr=0.01)
outputs=0
for epoch in range(500):
running_loss=0.0
optimizer.zero_grad() ## 如果不请空,那就可以做到大batchsize的梯度计算
if(epoch % 500 ==499):
with torch.no_grad(): ## 不计算误差梯度
outputs=net(x_test)
predict_y=torch.max(outputs,dim=1)[1] ## 返回概率最大的index
pass
save_path=""
torch.save(net.state_dict(),save_path) ## 保存网络的参数
net=LeNet()
net.load_state_dict(torch.load(""))
二、AlexNet
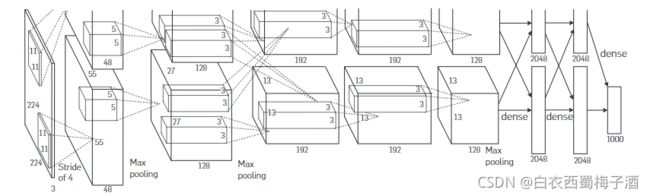
2.1 网络结构与亮点
亮点:
1.全部采用了非线性激活函数Relu
2.LRN(局部归一化层,后面证实无效果)overlapping pooling 网络的整体架构(pool的卷积核为stride < kernei_size,会出现重叠池化现象,有利于防止过拟合)
3.防止过拟合技术,数据增强和dropout(通过随机从256256的原始图像中截取224224的区域,来增加数据量,防止过拟合。)
2.2 代码
import torch
import torch.nn as nn
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torchvision.transforms as transforms
import torchvision.datasets as datasets
from tqdm import tqdm
class AlexNet(nn.Module):
def __init__(self,num_classes=5):
super(AlexNet,self).__init__()
self.features=nn.Sequential(
nn.Conv2d(3,48,kernel_size=11,stride=4,padding=2),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3,stride=2),
nn.Conv2d(48,128,kernel_size=5,padding=2),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3,stride=2),
nn.Conv2d(128,192,kernel_size=3,padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(192,192,kernel_size=3,padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(192,128,kernel_size=3,padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3,stride=2)
)
self.classifier=nn.Sequential(
nn.Dropout(p=0.5),
nn.Linear(128*6*6,4096),
nn.ReLU(inplace=True),
nn.Dropout(p=0.5),
nn.Linear(4096,4096),
nn.ReLU(inplace=True),
nn.Linear(4096,num_classes)
)
def forward(self,x):
x=self.features(x)
x=torch.flatten(x,start_dim=1)
x=self.classifier(x)
return x
device=torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
data_transform={
"train":transforms.Compose([transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize((0.5,0.5,0.5),(0.5,0.5,0.5))
]),
"val":transforms.Compose([transforms.Resize((224,224)),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])}
image_path=r'E:/MyCode/pythonProject1/MyPytorch/data_set/flower_data/'
train_data=datasets.ImageFolder(root=image_path+"train",transform=data_transform['train'])
validate_dataset = datasets.ImageFolder(root=image_path+"val",
transform=data_transform["val"])
val_num = len(validate_dataset)
validate_loader = torch.utils.data.DataLoader(validate_dataset,
batch_size=4, shuffle=False,
num_workers=0)
flower_index=train_data.class_to_idx
cla_dict=dict((val,key) for key,val in flower_index.items())
batch_size=32
data_loader=DataLoader(train_data,batch_size=batch_size,shuffle=True,num_workers=0)
net=AlexNet()
net.to(device)
loss_func=nn.CrossEntropyLoss()
optimizer=torch.optim.Adam(net.parameters(),lr=0.0002)
best_acc=0.0
epochs = 10
print(device)
for epoch in range(epochs):
net.train()
runnning_loss=0.0
train_steps = len(data_loader)
train_bar = tqdm(data_loader)
for step,data in enumerate(train_bar,start=0):
images,labels=data
optimizer.zero_grad()
output=net(images.to(device))
loss=loss_func(output,labels.to(device))
loss.backward()
optimizer.step()
runnning_loss+=loss.item()
train_bar.desc = "train epoch[{}/{}] loss:{:.3f}".format(epoch + 1,
epochs,
loss)
net.eval()
acc = 0.0 # accumulate accurate number / epoch
with torch.no_grad():
val_bar = tqdm(validate_loader)
for val_data in val_bar:
val_images, val_labels = val_data
outputs = net(val_images.to(device))
predict_y = torch.max(outputs, dim=1)[1]
acc += torch.eq(predict_y, val_labels.to(device)).sum().item()
val_accurate = acc / val_num
print('[epoch %d] train_loss: %.3f val_accuracy: %.3f' %
(epoch + 1, runnning_loss / train_steps, val_accurate))
if val_accurate > best_acc:
best_acc = val_accurate
三、VGG
3.1 网络结构与亮点
VGG网络的结构
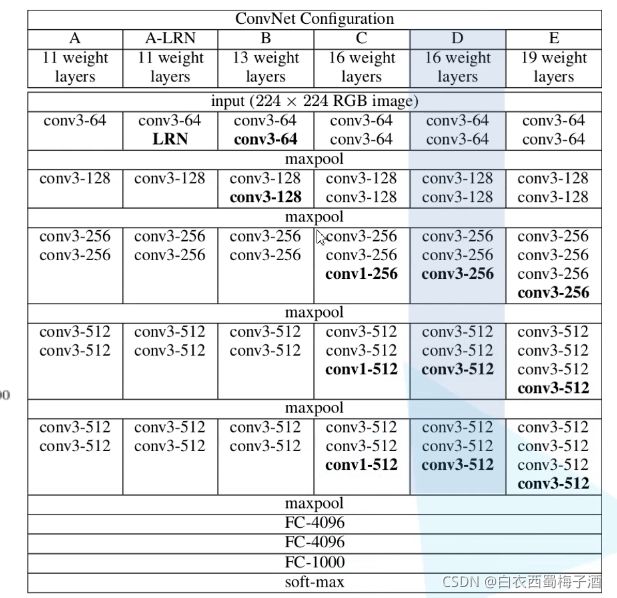
一般而言我们采用的是D的结构。其中conv层的stride=1,padding=1
maxpool的size=2,stride=2
相关亮点
1.通过堆叠多个33的卷积核来替代大尺度卷积核(减少所需参数),同时拥有更多的非线性变换,增加了CNN对特征的学习能力。(多个卷积层与非线性的激活层交替的结构,比单一卷积层的结构更能提取出深层的更好的特征。)
(因为多个非线性层会增加网络的深度,从而允许其学习更复杂的特征,并且计算成本更低)
比如通过堆叠两个33的卷积核可以替代55的卷积核。
通过堆叠三个33的卷积核可以替代7*7的卷积核。
上述的替代都有相同的感受野。
补充: CNN感受野 决定某一层输出结果中一个元素所对应的输入层的区域大小被称作感受野。通俗来说,即输出的feature map上的一个单元对应输入层上的区域大小。
感受野的计算公式如下:
2.在VGGNet的卷积结构中,引入1*1的卷积核,在不影响输入输出维度的情况下,引入非线性变换,增加网络的表达能力,降低计算量。
3.训练时,先训练级别简单(层数较浅)的VGGNet的A级网络,然后使用A网络的权重来初始化后面的复杂模型,加快训练的收敛速度。
4.采用了Multi-Scale的方法来训练和预测。可以增加训练的数据量,防止模型过拟合,提升预测准确率。
补充:多尺寸训练
每一幅图像单独的从[Smin,Smax]中随机选取S来进行尺寸缩放(Smin=256,Smax=512)。由于图像中的对象可能是各种尺寸的,因此在训练中采用这种方法是有利的。这同样可以看作是一种尺寸抖动(scale jittering)的训练集数据增强,使得一个单一模型能够识别各种尺寸的对象。考虑到训练速度,我们使用固定S=384预训练模型相同的配置对一个单尺度模型的所有层进行微调,来训练多尺度模型。
5.证明了局部归一化层的不起作用。
6.使用小卷积的好处:
(1)更少的参数量;(2)更多的非线性变换,使得CNN对特征的学习能力更强;
(3)隐式的正则化效果(收敛速度要快)。
可参考: OverFeat:Integrated Recognition, Localization and Detection using Convolutional Networks
参考文献
Very Deep Convolutional Networks for Large-Scale Image Recognition
3.2 代码
import torch
import torch.nn.functional as F
import numpy as np
import torch.nn as nn
class VGGNet(nn.Module):
def __init__(self,features,class_num=1000):
super(VGGNet,self).__init__()
self.features=features
self.classifier=nn.Sequential(
nn.Dropout(p=0.5),
nn.Linear(512*7*7,4096),
nn.ReLU(True),
nn.Dropout(p=0.5),
nn.Linear(2048,4096),
nn.ReLU(True),
nn.Linear(4096,class_num)
)
## 前向传播
def forward(self,x):
x=self.features(x)
x=torch.flatten(x,start_dim=1)
x=self.classifier(x)
return x
## 初始化参数
def _initialize_weights(self):
for m in self.modules():
if isinstance(m,nn.Conv2d):
nn.init.xavier_uniform(m.weight)
if m.bias is not None:
nn.init.constant_(m.bias,0)
if isinstance(m,nn.Linear):
nn.init.xavier_uniform(m.weight)
nn.init.constant_(m.bias,0)
## 生成提取特征网络结构
def make_feature(cfg:list):
layers=[]
## 默认输入channel
in_channels=3
for v in cfg:
if v=='M':
layers+=[nn.MaxPool2d(kernel_size=2,stride=(2,2))]
else:
conv2d=nn.Conv2d(in_channels,v,kernel_size=(3,3),padding=(1,1))
layers+=[conv2d,nn.ReLU(True)]
in_channels=v
## 非关键字参数传入参数
return nn.Sequential(*layers)
## VGGNet的配置参数字典
cfgs={
'VGG-11':[64,'M',128,'M',256,256,'M',512,512,'M',512,512,'M'],
'VGG-13':[64,64,'M',128,128,'M',256,256,'M',512,512,'M',512,512,'M'],
'VGG-16':[64,64,'M',128,128,'M',256,256,256,'M',512,512,512,'M',512,512,512,'M'],
'VGG-19':[64,64,'M',128,128,'M',256,256,256,256,'M',512,512,512,512,'M',512,512,512,512,'M']
}
def vgg(model_name='vgg-16',**kwargs):
try:
cfg=cfgs[model_name]
except:
raise BaseException
## kwargs 可变长度的字典变量
model=VGGNet(make_feature(cfg),**kwargs)
return model
## 采用gpu训练
device=torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
四、GoogLeNet
4.1 网络结构与亮点
网络的具体框架
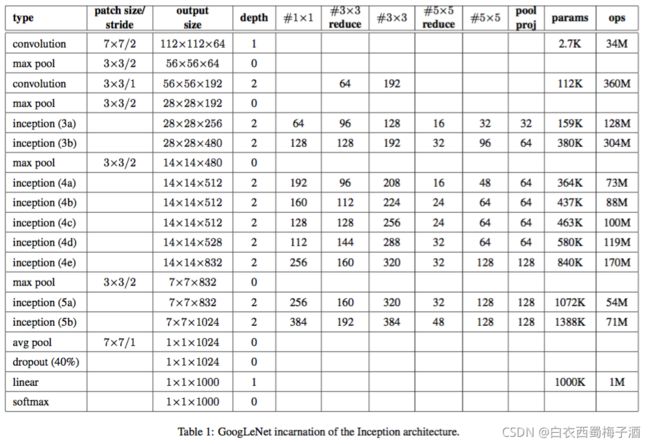
论文的动机或者思路:
直接提升深度神经网络的方法就是增加网络的尺寸,包括宽度和深度。深度也就是网络中的层数,宽度指每层中所用到的神经元的个数。但是这种简单直接的解决方式存在的两个重大的缺点。
(1)网络尺寸的增加也意味着参数的增加,也就使得网络更加容易过拟合。
(2)计算资源的增加。
该论文通过想到将全连接的方式改为稀疏连接来解决这两个问题。
数据集的概率分布由大又稀疏的深度神经网络表达时,网络拓扑结构可由逐层分析与输出高度相关的上一层的激活值和聚类神经元的相关统计信息来优化。(Provable bounds for learning some deep representations)
通常全连接是为了更好的优化并行计算,而稀疏连接是为了打破对称来改善学习,于是思索是否有方法能够既能保持网络结构的稀疏性,又能利用密集矩阵的高计算性能。通过已有文献可知将稀疏矩阵聚类为较为密集的子矩阵能提高计算性能,于是提出了Inception结构。
相关亮点:
1.增加了inception结构,在不增加计算负载的情况下,增加网络的宽度和深度。
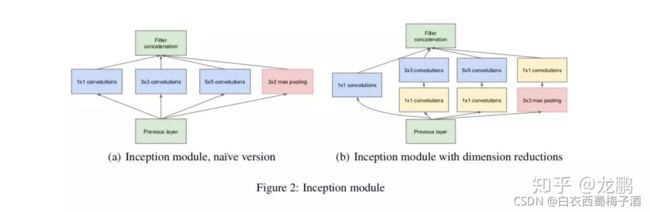
补充 对于inception结构的一些想法
(1)1*1卷积核:
在相同尺寸的感受野中叠加更多的卷积,能提取到更丰富的特征。(Network in Network)
同时降维来降低计算复杂性。
(2)在特征维度进行拼接的原因(融合不同尺度的特征信息)
利用稀疏矩阵分解成密集矩阵计算的原理来加快收敛速度
在多个尺度上同时进行卷积,能提取到不同尺度的特征。特征更为丰富也意味着最后分类判断时更加准确。
(通过多个卷积核提取图像不同尺度的信息,最后进行融合,可以得到图像更好的表征。)
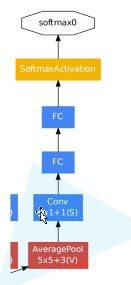
2.添加了两个辅助分类器帮助训练
3.丢弃了全连接层层,使用平均池化层(大大减少模型的参数)
参考文献
Going Deeper with Convolutions
4.2 代码
import telnetlib
import torch
import torchvision.transforms as transforms
import torch.nn.functional as F
import torch.nn as nn
import torchvision.datasets as datasets
from torch.utils.data import DataLoader
from tqdm import tqdm
## 定义GooLeNet类
class GooLeNet(nn.Module):
def __init__(self,num_classes=1000,use_aux=True):
super(GooLeNet, self).__init__()
self.use_aux=use_aux
self.conv1=BasicConv2d(3,64,kernel_size=7,stride=2,padding=3)
## ceil_mode 如果计算为小数,则向上取整, false 为向下取整
self.maxPool1=nn.MaxPool2d(3,stride=2,ceil_mode=True)
self.conv2=BasicConv2d(64,64,kernel_size=1)
self.conv3=BasicConv2d(64,192,kernel_size=3,padding=1)
self.maxPool2=nn.MaxPool2d(3,stride=2,ceil_mode=True)
self.inception3a=Inception(192,64,96,128,16,32,32)
self.inception3b=Inception(256,128,128,192,32,96,64)
self.maxPool3=nn.MaxPool2d(3,stride=2,ceil_mode=True)
self.inception4a=Inception(480,192,96,208,16,48,64)
self.inception4b=Inception(512,160,112,224,24,64,64)
self.inception4c=Inception(512,128,128,256,24,64,64)
self.inception4d=Inception(512,112,144,288,32,64,64)
self.inception4e=Inception(528,256,160,320,32,128,128)
self.maxPool4=nn.MaxPool2d(kernel_size=3,stride=2,ceil_mode=True)
self.inception5a=Inception(832,256,160,320,32,128,128)
self.inception5b=Inception(832,384,192,384,48,128,128)
if use_aux:
self.aux1=AuxiliaryClassifier(512,num_classes)
self.aux2=AuxiliaryClassifier(528,num_classes)
## 自适应 给定输出矩阵的高和宽
self.avgPool=nn.AdaptiveAvgPool2d((1,1))
self.dropout=nn.Dropout(0.4)
self.fc=nn.Linear(1024,num_classes)
def forward(self,x):
x=self.conv1(x)
x=self.maxPool1(x)
x=self.conv2(x)
x=self.conv3(x)
x = self.maxPool2(x)
x=self.inception3a(x)
x=self.inception3b(x)
x=self.maxPool3(x)
x=self.inception4a(x)
if self.training and self.use_aux:
aux1=self.aux1(x)
x=self.inception4b(x)
x=self.inception4c(x)
x=self.inception4d(x)
if self.training and self.use_aux:
aux2=self.aux2(x)
x=self.inception4e(x)
x=self.maxPool4(x)
x=self.inception5a(x)
x=self.inception5b(x)
x=self.avgPool(x)
x=torch.flatten(x,1)
x=self.dropout(x)
x=self.fc(x)
if self.training and self.use_aux:
return x,aux2,aux1
return x
## 定义辅助分类器
class AuxiliaryClassifier(nn.Module):
def __init__(self,in_channel,num_classes):
super(AuxiliaryClassifier,self).__init__()
self.avgPool=nn.AvgPool2d(kernel_size=5,stride=3)
self.conv=BasicConv2d(in_channel,128,kernel_size=1)
self.fc1=nn.Linear(2048,1024)
self.fc2=nn.Linear(1024,num_classes)
def forward(self,x):
x=self.avgPool(x)
x=self.conv(x)
x=torch.flatten(x,start_dim=1)
## self.training 可以由model.train() 或者model.eval() 来修改
x=F.dropout(x,p=0.7,training=self.training)
x=F.relu(self.fc1(x),inplace=True)
x=F.dropout(x,p=0.7,training=self.training)
x=self.fc2(x)
return x
## 定义Inception 结构
## ch1v1 等为对应的卷积核个数
class Inception(nn.Module):
def __init__(self,in_channels,ch1v1,ch3v3red,ch3v3,ch5v5red,ch5v5,pool_proj):
super(Inception,self).__init__()
self.branch1=BasicConv2d(in_channels,ch1v1,kernel_size=1)
self.branch2=nn.Sequential(
BasicConv2d(in_channels,ch3v3red,kernel_size=1),
BasicConv2d(ch3v3red,ch3v3,kernel_size=3,padding=1)
)
self.branch3=nn.Sequential(
BasicConv2d(in_channels,ch5v5red,kernel_size=1),
BasicConv2d(ch5v5red,ch5v5,kernel_size=5,padding=2)
)
self.branch4=nn.Sequential(
nn.MaxPool2d(kernel_size=3,stride=1,padding=1),
BasicConv2d(in_channels,pool_proj,kernel_size=1)
)
def forward(self,x):
branch1=self.branch1(x)
branch2=self.branch2(x)
branch3=self.branch3(x)
branch4=self.branch4(x)
outputs=[branch1,branch2,branch3,branch4]
## 输入参数为 矩阵, 合并的维度 这里是channel
return torch.cat(outputs,1)
## 定义基础的卷积层(包括激活函数)
class BasicConv2d(nn.Module):
def __init__(self,in_channels,out_channels,**kwargs):
super(BasicConv2d,self).__init__()
self.conv=nn.Conv2d(in_channels,out_channels,**kwargs)
## inplace 增加计算量来减少内存使用
self.relu=nn.ReLU(inplace=True)
def forward(self,x):
x=self.conv(x)
x=self.relu(x)
return x
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
data_transform = {
"train": transforms.Compose([transforms.RandomResizedCrop(224),
transforms.ToTensor(),
transforms.RandomHorizontalFlip(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))]),
"eval": transforms.Compose([transforms.RandomSizedCrop((224, 224)),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
}
image_path = r'E:/MyCode/pythonProject1/MyPytorch/data_set/flower_data/'
train_data = datasets.ImageFolder(root=image_path + "train", transform=data_transform['train'])
eval_data = datasets.ImageFolder(root=image_path + "val", transform=data_transform['eval'])
train_num = len(train_data)
eval_num = len(eval_data)
batch_size = 32
train_loader = DataLoader(train_data, batch_size=batch_size, shuffle=True, num_workers=0)
validate_loader = torch.utils.data.DataLoader(eval_data,
batch_size=batch_size, shuffle=False,
num_workers=0)
##
net = GooLeNet(num_classes=5)
epoches = 10
loss_func = nn.CrossEntropyLoss()
net.to(device)
optimizer = torch.optim.Adam(net.parameters(), lr=0.0002)
train_steps = len(train_loader)
for epoch in range(epoches):
net.train()
running_loss = 0.0
train_bar = tqdm(train_loader)
for step, data in enumerate(train_bar,start=0):
optimizer.zero_grad()
images,labels=data
output,aux1,aux2=net(images.to(device))
loss1=loss_func(output,labels.to(device))
loss2=loss_func(aux1,labels.to(device))
loss3=loss_func(aux2,labels.to(device))
loss = loss1 + loss2 * 0.3 + loss3 * 0.3
loss.backward()
optimizer.step()
running_loss += loss.item()
train_bar.desc = "train epoch[{}/{}] loss:{:.3f}".format(epoch + 1,
epoches,
loss)
net.eval()
acc = 0.0
with torch.no_grad():
val_bar = tqdm(validate_loader)
for data in val_bar:
val_images, val_labels = data
output = net(val_images.to(device))
predict_y = torch.max(output, dim=1)[1]
acc += torch.eq(predict_y, val_labels.to(device)).sum().item()
val_accurate = acc / eval_num
print('[epoch %d] train_loss: %.3f val_accuracy: %.3f' %
(epoch + 1, running_loss / train_steps, val_accurate))
五、ResNet
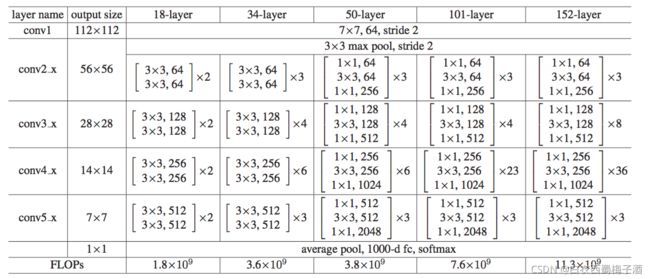
5.1 网络结构与亮点
论文的一些思路想法
1.当神经网络更深时,会出现梯度爆炸/消失的情况。出现该情况的原因并非是神经网络的过拟合,而是在适当的深度模型上添加更多的层会导致更高的训练误差,所导致的。
论文采用残差块以及跳跃链接的方式来解决上述问题。即提出residual层,明确地让这些层拟合残差映射,而不是希望每几个堆叠的层直接拟合期望的基础映射。
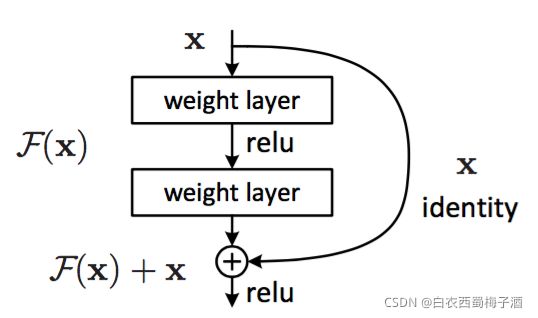
跳跃连接既不增加额外的参数也不增加计算复杂度。
补充: 残差表示:
在图像识别中,VLAD是一种通过关于字典的残差向量进行编码的表示形式,Fisher矢量可以表示为VLAD的概率版本。它们都是图像检索和图像分类中强大的浅层表示。对于矢量量化,编码残差矢量被证明比编码原始矢量更有效。
跳跃链接: 训练多层感知机(MLP)的早期实践是添加一个线性层来连接网络的输入和输出。
残差结构更易于学习:
1.如果恒等映射是最优的,求解器可能简单地将多个非线性连接的权重推向零来接近恒等映射。
2.在实际情况下,恒等映射不太可能是最优的,但是我们的重构可能有助于对问题进行预处理。
残差:
在线性拟合中的残差说的是数据点距离拟合直线的函数值的差,那么这里我们可以类比,这里的X就是我们的拟合的函数,而H(x)的就是具体的数据点,那么我通过训练使的拟合的值加上F(x)的就得到具体数据点的值,因此这 F(x)的就是残差了,还是画个图吧,如下图:
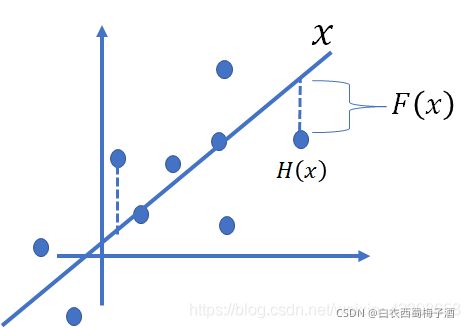
如果已经学习到较饱和的准确率(或者当发现下层的误差变大时),那么接下来的学习目标就转变为恒等映射的学习,也就是使输入x近似于输出H(x),以保持在后面的层次中不会造成精度下降。
在上图的残差网络结构图中,通过“shortcut connections(捷径连接)”的方式,直接把输入x传到输出作为初始结果,输出结果为H(x)=F(x)+x,当F(x)=0时,那么H(x)=x,也就是上面所提到的恒等映射。于是,ResNet相当于将学习目标改变了,不再是学习一个完整的输出,而是目标值H(X)和x的差值,也就是所谓的残差F(x) := H(x)-x,因此,后面的训练目标就是要将残差结果逼近于0,使到随着网络加深,准确率不下降。
补充: 设计网络的规则:
1.对于输出feature map大小相同的层,有相同数量的filters,即channel数相同;
2.当feature map大小减半时(池化),filters数量翻倍。
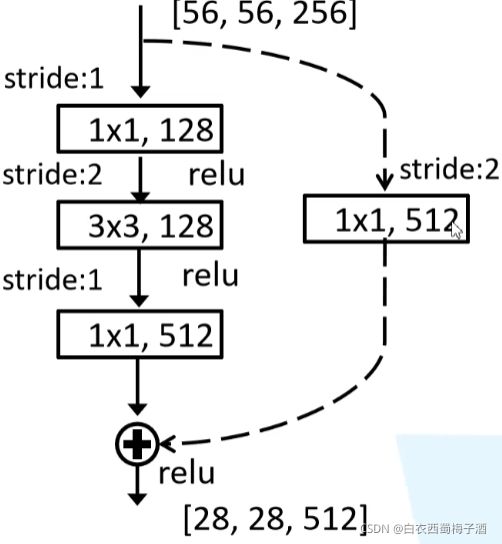
对于残差网络,维度匹配的shortcut连接为实线,反之为虚线。维度不匹配时,同等映射有两种可选方案:1)直接通过zero padding 来增加维度(channel)。
2)乘以W矩阵投影到新的空间。实现是用1x1卷积实现的,直接改变1x1卷积的filters数目。这种会增加参数。
亮点
1.相比传统的卷积神经网络如VGG复杂度降低,需要的参数下降。
2.可以做到更深,不会出现梯度弥散的问题。
3.优化简单,分类准确度加深由于使用更深的网络。
4.解决深层次网络的退化问题。
参考文献:
Deep Residual Learning for Image Recognition
5.2 代码
import torch
import torchvision
import torch.nn.functional as F
import torch.nn as nn
from torch.utils.data import DataLoader
import torch.optim as optim
class ResNet(nn.Module):
## block 所使用的的块, 每个conv的残差块的个数 列表
def __init__(self,block,block_num,num_classes=1000):
super(ResNet,self).__init__()
## 根据论文默认为64
self.in_channels=64
self.conv1=nn.Conv2d(3,self.in_channels,kernel_size=7,stride=2,padding=3,bias=False)
self.bn1=nn.BatchNorm2d(self.in_channels)
self.relu=nn.ReLU(inplace=True)
## 需要为原来的一般,默认向下取整
self.maxpool=nn.MaxPool2d(kernel_size=3,stride=2,padding=1)
self.layer1=self._make_layer(block,64,block_num[0])
self.layer2=self._maker_layer(block,128,block_num[1],stride=2)
self.layer3=self._maker_layer(block,256,block_num[2],stride=2)
self.layer4=self._maker_layer(block,512,block_num[3],stride=2)
self.avgpool=nn.AdaptiveAvgPool2d((1,1))
self.fc=nn.Linear(512*block.expansion,num_classes)
def _maker_layer(self,block,channel,block_num,stride=1):
downsample=None
if stride!=1 or self.in_channels !=channel*block.expansion:
downsample=nn.Sequential(
nn.Conv2d(self.in_channels,channel*block.expansion,kernel_size=1,stride=stride,bias=False),
nn.BatchNorm2d(channel*block.expansion)
)
layers=[]
layers.append(block(self.in_channels,channel,downsample=downsample,stride=stride))
self.in_channels=channel*block.expansion
for _ in range(1,block_num):
layers.append(block(self.in_channels,channel))
return nn.Sequential(*layers)
def forward(self,x):
x=self.conv(x)
x=self.bn1(x)
x=self.relu(x)
x=self.maxpool(x)
x=self.layer1(x)
x=self.layer2(x)
x=self.layer3(x)
x=self.layer4(x)
x=self.avgpool(x)
x=torch.flatten(x,1)
x=self.fc(x)
return x
## 18 30 层的基本残差块
class BasicBlock(nn.Module):
## 残差结构的卷积核个数是否变动 ,如果为1则不变
expansion=1
## downsample 下采样 捷径是否有对应的修改维度的操作
def __init__(self,in_channels,out_channels,stride=1,downsample=None):
super(BasicBlock,self).__init__()
self.conv1=nn.Conv2d(in_channels=in_channels,out_channels=out_channels,kernel_size=3,stride=stride,padding=1,bias=False)
self.bn1=nn.BatchNorm2d(out_channels)
self.relu=nn.ReLU()
self.conv2=nn.Conv2d(in_channels=out_channels,out_channels=out_channels,kernel_size=3,stride=1,padding=1,bias=False)
self.bn2=nn.BatchNorm2d(out_channels)
self.downsample=downsample
def forward(self,x):
identity=x
if self.downsample is not None:
identity=self.downsample(x)
out=self.conv1(x)
out=self.bn1(out)
out=self.relu(out)
out=self.conv2(out)
out=self.bn2(out)
out+=identity
out=self.relu(out)
return out
## 50层的基本类
class Bottleneck(nn.Module):
## 类似的由论文可知 50层,101层,152层的每个残差结构的最后一个的卷积核个数为之前的4倍,所以为4
expansion=4
def __init__(self,in_channels,out_channels,stride=1,downsample=None):
super(Bottleneck,self).__init__()
self.conv1=nn.Conv2d(in_channels=in_channels,out_channels=out_channels,kernel_size=1,stride=1,bias=False)
self.bn1=nn.BatchNorm2d(out_channels)
self.conv2=nn.Conv2d(in_channels=out_channels,out_channels=out_channels,kernel_size=3,stride=stride,padding=1,bias=False)
self.bn2=nn.BatchNorm2d(out_channels)
self.conv3=nn.Conv2d(in_channels=out_channels,out_channels=out_channels*self.expansion,kernel_size=1,stride=1,bias=False)
self.bn3=nn.BatchNorm2d(out_channels*self.expansion)
self.relu=nn.ReLU(inplace=True)
self.downsample=downsample
def forward(self,x):
identity=x
if self.downsample is not None:
identity=self.downsample(x)
out=self.conv1(x)
out=self.bn1(out)
out=self.relu(out)
out=self.conv2(out)
out=self.bn2(out)
out=self.relu(out)
out=self.conv3(out)
out=self.bn3(out)
out+=identity
out=self.relu(out)
return out
def resnet34(num_classes=1000):
return ResNet(BasicBlock,[3,4,6,4],num_classes=num_classes)
def resnet101(num_classes=1000):
return ResNet(Bottleneck,[3,4,23,3],num_classes=num_classes)
补充
ResNet 有两种残差结构,一种是虚线残差(因为输入与输出的维度不同,所以在shortcut上需要通过1*1的矩阵进行维度变换)另一种是实线残差(输入输出维度相同,之间线性组合)
同时在ResNet 层数18.24层,conv2的输入与输出相同所以为实线,但是其余的则不相同,在该conv2的第一个残差块需要用虚线残差。
同理,后续的conv3,conv4,conv5的第一个残差结构都需要使用虚线残差。
六、MobileNet
6.1 网络结构与亮点
MobileNet_v1网络结构:
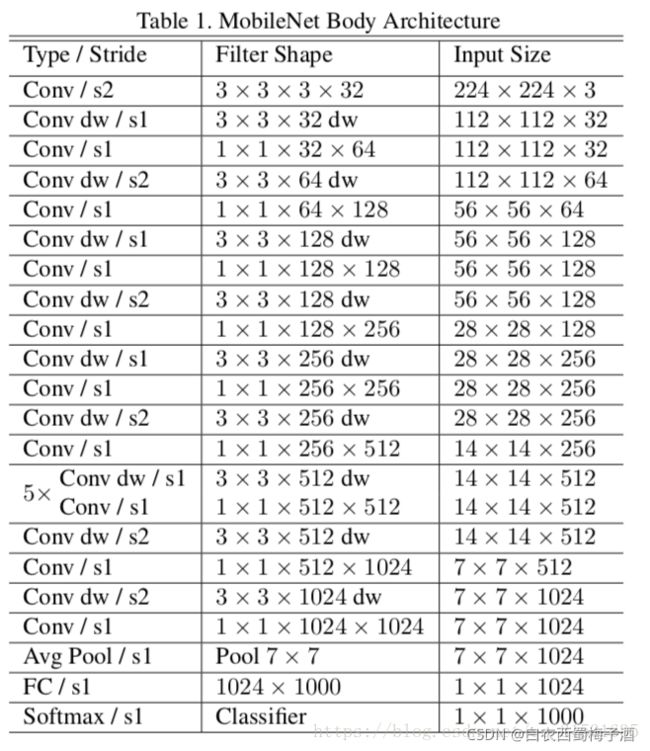
论文的一些思路与动机:
为了能够在移动设备上完成相应的计算机视觉方面的实现,需要能够在不大幅度降低准确率的情况下,大量减少计算所需的参数。
由此提出了深度可分离卷积,同时增加两个模型收缩超参数即宽度乘法器和分辨率乘法器。
亮点:
1.深度可分离卷积(Depthwise Separable Conv):
深度卷积(Depthwise Conv,DW)对每个通道使用一种卷积核,即第m个卷积核应用于F中的第m个通道来产生第m个通道的卷积输出特征图。由此可以大幅降低所需的参数量。
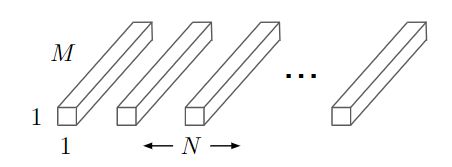
但是,深度卷积只对输入通道进行卷积,没有对其进行组合来产生新的特征。由此,需要在下一层来加上一个11的卷积来对深度卷积的输出计算一个线性组合从而产生新的特征。(Pointwise Conv,PW)
通过深度卷积加上1x1卷积的逐点卷积的结合而产生的深度可分离卷积,在理论上能够比标准卷积少了8-9倍的计算量,同时只有极小的准确率下降。
2.增加了超参数宽度乘法器α,分辨率乘法器β。
其中宽度乘法器α:主要是对每一层薄化,使其输入通道数与输出通道数同为α倍,一般设置为1\0.75\0.5\0.25。(通过实验可知薄化操作比浅化操作效果更好)
分辨率乘法器β:设置输入的分辨率大小,即βDF。
补充 深度可分离卷积 用于空间滤波的轻量深度深度卷积和用于特征生成的较重的1x1点向卷积。
MobileNet_v2:
论文的一些思路和动机:
优化MobileNet_v1,希望能够在更小的数据量的情况下,有更好的准确性。
网络结构:
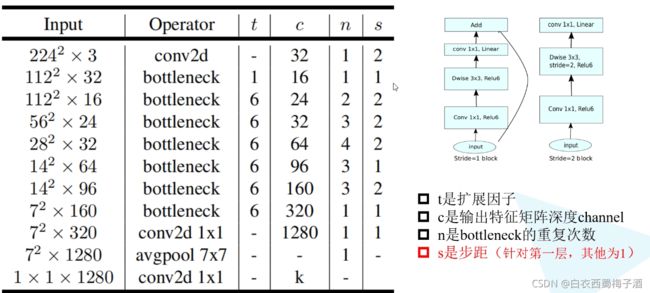
亮点:
1.倒残差结构(inverted residual structure):首先将输入从低维扩展到高维,然后用深度卷积做过滤,再将其从高维压缩到低维。同时采用relu6激活函数。
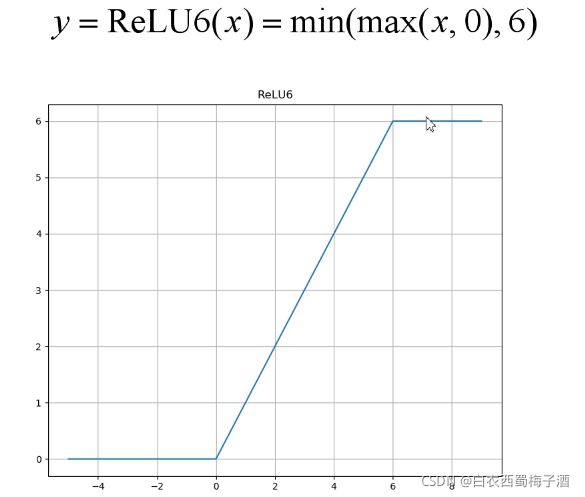
2.Linear Bottlenecks
我们认为在神经网络中,相应的manifold of interest(被翻译为兴趣流行,即通过一连串的卷积和激活层形成),是可以嵌入到低维子空间的。
补充:从某种意义上来说,MobileNetv1的宽度控制因子α也是控制激活空间的维度,使得manifold of interest 横跨整个空间。
但是如果当前的激活空间内的manifold of interest 有较高的完整度,那么经过Relu会丢失掉部分的信息。

从上图,我们可以看到,对于低纬度的,Relu会丢失大量的信息。
由此,我们知道,如果我们想要让manifold of interest 能够较完整的保留在低维空间,那么Relu很可能会过滤掉很多的有用信息,而对于没有过滤的部分,relu的作用是一个线性的分类器。
于是论文中提出使用linear bottleneck来代替Relu的非线性激活变换。(在结构的最后一个PW后不通过relu激活函数而是直接输出)
补充:如果manifold of interest 可通过激活空间嵌入到显著的低维子空间,那么通常ReLU变换可保留信息
参考文献
1.MobileNets: Efficient Convolutional Neural Networks for MobileVision Applications
2.MobileNetV2: Inverted Residuals and Linear Bottlenecks
6.2 代码
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import torch.optim as optim
class ConvBNReLu(nn.Sequential):
def __init__(self,in_channels,out_channels,kernel_size=3,stride=1,groups=1):
padding=(kernel_size-1)//2
super(ConvBNReLu,self).__init__(nn.Conv2d(in_channels=in_channels,out_channels=out_channels,kernel_size=kernel_size,stride=stride,groups=groups,bias=False,padding=padding),
nn.BatchNorm2d(out_channels),
nn.ReLU6(inplace=True)
)
class InvertResidual(nn.Module):
## expand_ratio 扩展因子
def __init__(self,in_channel,out_channel,stride,expand_ratio):
super(InvertResidual,self).__init__()\
## tk
hidden_channel=in_channel*expand_ratio
## 是否使用shortcut
self.use_shortcut=stride==1 and in_channel==out_channel
layers=[]
if expand_ratio!=1:
## 添加一个1*1的升维卷积
layers.append(ConvBNReLu(in_channel,hidden_channel,kernel_size=1))
layers.extend([
##dw卷积
ConvBNReLu(hidden_channel,hidden_channel,kernel_size=3,stride=stride,groups=hidden_channel),
## 使用的是线性激活函数
nn.Conv2d(hidden_channel,out_channel,kernel_size=1,bias=False),
nn.BatchNorm2d(out_channel)
])
self.conv=nn.Sequential(*layers)
def forward(self,x):
if self.use_shortcut:
return x+self.conv(x)
else:
return self.conv(x)
## min_ch 采用的channel的最小个数
def _make_divisible(ch,divisor=8,min_ch=None):
if min_ch is None:
min_ch=divisor
## 将输入的channels 调整到最近的8的整数倍的数值 当ch=12 时为16
new_ch=max(min_ch,int(ch+divisor/2)//divisor*divisor)
## 调整后的channel不能减少超过10%
if new_ch<0.9*ch:
new_ch+=divisor
return new_ch
class MobileNetV2(nn.Module):
def __init__(self,num_classes=1000,alpha=1.0,round_nearest=8):
super(MobileNetV2,self).__init__()
block=InvertResidual
## 将输入的维度调整维roundnestest的整数倍
input_channels=_make_divisible(32*alpha,round_nearest)
last_channels=_make_divisible(1280*alpha,round_nearest)
## 残差块的参数设置
inverted_residual_setting=[
[1,16,1,1],
[6,24,2,2],
[6,32,3,2],
[6,64,4,2],
[6,96,3,1],
[6,160,3,2],
[6,320,1,1],
]
features=[]
features.append(ConvBNReLu(3,input_channels,stride=2))
for t,c,n,s in inverted_residual_setting:
## 调整每层的输出channel
output_channel=_make_divisible(c*alpha,round_nearest)
for i in range(n):
## s是每个残差结构第一层的stride,后续的都为1
stride=s if i==0 else 1
features.append(block(input_channels,output_channel,stride,expand_ratio=t))
input_channels=output_channel
features.append(ConvBNReLu(input_channels,last_channels,1))
self.features=nn.Sequential(*features)
self.avgpool=nn.AdaptiveAvgPool2d((1,1))
## 全连接层
## 或者可以按照论文结构直接使用Conv2d ,Conv2d与linear两者效果一样
# self.classifier=nn.Sequential(
# nn.Conv2d(last_channels,num_classes,kernel_size=1,stride=1)
# )
self.classifier=nn.Sequential(
nn.Dropout(0.2),
nn.Linear(last_channels,num_classes)
)
def forward(self,x):
x=self.features(x)
x=self.avgpool(x)
x=torch.flatten(x,1)
x=self.classifier(x)
return x
补充:并非每个残差结构都有shortcut,而是当stride=1且输入特征矩阵与输出特征矩阵shape相同时才有shortcut连接。