卷积神经网络参数量和计算量的计算
前言
本文主要是介绍卷积神经网络模型的中的参数量和计算量公式推导及其计算公式。先区分FLOPS和FLOPs,再介绍stride = 1情况下CNN的参数量和计算量。文末的Reference1附上不同stride的计算CNN参数量。
区分FLOPS和FLOPs
- FLOPS 注意全部大写 是floating point of per second的缩写,意指每秒浮点运算次数。可以理解为计算速度,用来衡量硬件的性能。
- FLOPs 是floating point of operations的缩写,是浮点运算次数,理解为计算量,可以用来衡量算法/模型复杂度。
同一硬件,它的最大FLOPS(每秒运算浮点数代表着硬件性能,区分FLOPs)是相同的,不同网络,处理每张图片所需的FLOPs(浮点操作数)是不同的,所以同一硬件处理相同图片所需的FLOPs越小,相同时间内,就能处理更多的图片,速度也就越快,处理每张图片所需的FLOPs与许多因素有关,比如你的网络层数,参数量,选用的激活函数等等,这里仅谈一下网络的参数量对其的影响,一般来说参数量越低的网络,FLOPs会越小,保存模型所需的内存小,对硬件内存要求比较低,因此比较对嵌入式端较友好。
普通卷积的参数量(parameters)和计算量(FLOPs)
先放一张图,理解了这张图对于下面公式的推导很有帮助。
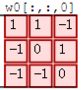
如上图,注意:上图有两个卷积核,分别为Filter W0和Filter W1。输入通道数 C i C_i Ci为3,输出通道数 C o C_o Co为2,输出通道数和卷积核个数是相等的,也等于偏置的个数。
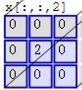
其中,Output Volume中的o[:, :, 0]的输出结果1的计算方法为:
$0 * 1+ 0 * 1 + 0 * -1 + 0 * -1 + 0 * 0 + 1 * 1 + 0 * -1 + 0 * -1 + 1 * 0 + $

$-1 * 0 + 0 * 0 + -1 * 0 + 0 * 0 +0 * 1 + -1 * 1 + 1 * 0 + 0 * 0 + 0 * 2 + $
$0 * 0 + 1 * 0 + 0 * 0 + 1 * 0 + 0 * 2 + 1 * 0 + 0 * 0 + -1 * 0 + 1 * 0 + $
ok,如果能理解到这,下面的公式推导就会简单很多。注意:以下的计算均默认stride = 1和“same”填充,stride > 1的情况在Reference1里面有详细的公式推导。
1.对CNN而言,每个卷积层的参数量计算如下:
![]()
其中表示 C o C_o Co输出通道数, C i C_i Ci表示输入通道数, k w k_w kw表示卷积核宽, k h k_h kh表示卷积核高。
k w ∗ k h ∗ C i k_w*k_h*C_i kw∗kh∗Ci括号内的表示一个卷积核的权重数量,+1表示bias,括号表示一个卷积核的参数量, C o C_o Co表示该层有 C o C_o Co个卷积核。
若卷积核是方形的,即 k w = k h = k k_w=k_h=k kw=kh=k,则上式变为:
![]()
需要注意的是,使用Batch Normalization时不需要bias,此时计算式中的+1项去除。
2.对CNN而言,每个卷积层的运算量计算如下:
![]()
FLOPs是英文floating point operations的缩写,表示浮点运算量,中括号内的值表示卷积操作计算出feature map中一个点所需要的运算量(乘法和加法), C i ∗ k w ∗ k h C_i*k_w*k_h Ci∗kw∗kh 表示一次卷积操作中的乘法运算量, C i ∗ k w ∗ k h − 1 C_i*k_w*k_h-1 Ci∗kw∗kh−1表示一次卷积操作中的加法运算量,+ 1 表示bias,W和H分别表示feature map的长和宽, ∗ C o ∗ W ∗ H *C_o*W*H ∗Co∗W∗H表示feature map的所有元素数。
若是方形卷积核,即 k w = k h = k k_w=k_h=k kw=kh=k,则有:
![]()
上面是乘运算和加运算的总和,将一次乘运算或加运算都视作一次浮点运算。
在计算机视觉论文中,常常将一个’乘-加’组合视为一次浮点运算,英文表述为’Multi-Add’,运算量正好是上面的算法减半,此时的运算量为:
![]()
全连接层的参数量(parameters)和计算量(FLOPs)
在 CNN 结构中,经多个卷积层和池化层后,连接着1个或1个以上的全连接层.与 MLP 类似,全连接层中的每个神经元与其前一层的所有神经元进行全连接.全连接层可以整合卷积层或者池化层中具有类别区分性的局部信息.为了提升 CNN 网络性能,全连接层每个神经元的激励函数一般采用 ReLU 函数。最后一层全连接层的输出值被传递给一个输出,可以采用 softmax 逻辑回归(softmax regression)进行 分 类,该层也可 称为 softmax 层(softmax layer).对于一个具体的分类任务,选择一个合适的损失函数是十分重要的,CNN 有几种常用的损失函数,各自都有不同的特点.通常,CNN 的全连接层与 MLP 结构一样,CNN 的训练算法也多采用BP算法。
全连接层的每一个结点都与上一层的所有结点相连,用来把前边提取到的特征综合起来。由于其全相连的特性,一般全连接层的参数也是最多的。例如在VGG16中,第一个全连接层FC1有4096个节点,上一层POOL2是77512 = 25088个节点,则该传输需要4096*25088个权值,需要耗很大的内存。
其中,x1、x2、x3为全连接层的输入,a1、a2、a3为输出,
a 1 = W 1 1 ∗ x 1 + W 1 2 ∗ x 2 + W 1 3 ∗ x 3 + b 1 a_1 = W_11 * x_1 + W_12* x_2 + W_13 * x_3 + b_1 a1=W11∗x1+W12∗x2+W13∗x3+b1
a 2 = W 2 1 ∗ x 1 + W 2 2 ∗ x 2 + W 2 3 ∗ x 3 + b 2 a_2 = W_21 * x_1 + W_22* x_2 + W_23 * x_3 + b_2 a2=W21∗x1+W22∗x2+W23∗x3+b2
a 3 = W 3 1 ∗ x 1 + W 3 2 ∗ x 2 + W 3 3 ∗ x 3 + b 3 a_3 = W_31 * x_1 + W_32* x_2 + W_33 * x_3 + b_3 a3=W31∗x1+W32∗x2+W33∗x3+b3
其实现在全连接层已经基本不用了,CNN基本用FCN来代表,可用卷积层来实现全连接层的功能。
3.对全连接层而言,其参数量非常容易计算:
![]()
值得注意的是,最初由feature map flatten而来的向量视为第一层全连接层,即此处的 I I I。
可以这样理解上式:每一个输出神经元连接着所有输入神经元,所以有 I I I个权重,每个输出神经元还要加一个bias。
也可以这样理解:每一层神经元(O这一层)的权重数为I×O,bias数量为O。
4.对全连接层而言,其运算量计算如下:
![]()
其中 I = i n p u t n e r o n s , O = o u t p u t n e r o n s I = input\ nerons, O = output\ nerons I=input nerons,O=output nerons
中括号的值表示计算出一个神经元所需的运算量,第一个 I I I表示乘法运算量, I − 1 I-1 I−1表示加法运算量,+1表示bias, × O ×O ×O表示计算O个神经元的值。
分组卷积

将图一卷积的输入feature map分成组,每个卷积核也相应地分成组,在对应的组内做卷积,如上图2所示,图中分组数,即上面的一组feature map只和上面的一组卷积核做卷积,下面的一组feature map只和下面的一组卷积核做卷积。每组卷积都生成一个feature map,共生成个feature map。
-
输入每组feature map尺寸: W ∗ H ∗ C g W * H * \frac{C}{g} W∗H∗gC ,共有g组;
-
单个卷积核每组的尺寸: k ∗ k ∗ C g k * k * \frac{C}{g} k∗k∗gC , 一个卷积核被分成了g组;
-
输出feature map尺寸: W ′ ∗ H ′ ∗ g W' * H' * g W′∗H′∗g , 共生成g个feature map。
分组卷积时的参数量和运算量:
-
参数量: p a r a m s = k 2 ∗ C g ∗ g = k 2 C params = k^2 * \frac{C}{g} * g = k^2C params=k2∗gC∗g=k2C
-
运算量: F L O P s = k 2 ∗ C g ∗ W ′ ∗ H ′ ∗ g = k 2 C W ′ H ′ FLOPs = k^2 * \frac{C}{g} * W' * H' * g = k^2CW'H' FLOPs=k2∗gC∗W′∗H′∗g=k2CW′H′
group conv常用在轻量型高效网络中,因为它用少量的参数量和运算量就能生成大量的feature map,大量的feature map意味着能够编码更多的信息!
深度分离卷积
从分组卷积的角度来看,分组数g就像一个控制旋钮,最小值是1,此时g = 1的卷积就是普通卷积;最大值是输入feature map的通道数C,此时g=C的卷积就是depthwise sepereable convolution,即深度分离卷积,又叫逐通道卷积。
如上图所示,深度分离卷积是分组卷积的一种特殊形式,其分组数为C,其中是feature map的通道数。即把每个feature map分为一组,分别在组内做卷积,每组内的单个卷积核尺寸为,组内一个卷积核生成一个feature map。这种卷积形式是最高效的卷积形式,相比普通卷积,用同等的参数量和运算量就能够生成个feature map,而普通卷积只能生成一个feature map。
所以此时的参数量和运算量和上面的分组卷积一样。
借助工具自动计算FLOPs值
推荐两个工具pytorch-OpCounter和torchstat,调用方法很简单,具体看github项目里面的readme。
1.pytorch-OpCounter
2.torchstat
总结
对比上面的参数量(parameters)和计算量(FLOPs)的计算结果,可以得到结论:
- FLOPs = paras * H * W
其中的H和W分别为feature map的尺寸。
这里只是给了几种常用卷积神经网络的参数量(parameters)和计算量(FLOPs)的公式推导,一个完整的神经网路还包括激活层,Batch Normalization等等,这些层肯定也是有FLOPs的。
本人水平有限,如有错误,望及时指出,谢谢!
Reference
1.不同stride下CNN参数计算
2.自动计算模型参数量、FLOPs、乘加数以及所需内存等数据
3.group convolution (分组卷积)详解
4.CNN 模型所需的计算力(flops)和参数(parameters)数量是怎么计算的?
5.目标检测的性能评价指标
6.卷积神经网络模型参数量和运算量计算方法
长按关注我的公众号哦!