pytorch常用优化器总结(包括warmup介绍及代码实现)

优化算法大致分为：梯度下降法，动量优化法，自适应学习率三种。

梯度下降法

梯度下降 GD

通过loss对$\omega$的一阶导数来找下降方向，并且以迭代的方式来更新参数。

$$W_{t+1}=W_t-\eta \nabla L(W_t)$$, 其中$\eta$为学习率。

随机梯度下降 （SGD)

均匀的随机选择其中一个样本（$X^{(i)},Y^{(i)}$)，用它代表整个样本，即把它的值乘以N，就相当于获得了梯度的无偏估计值。

公式：${\mathbf{W}}_{t+1}={\mathbf{W}}_t-\eta N\nabla J\left({\mathbf{W}}_t,X^{(i)},Y^{(i)}\right)$

小批量梯度下降法（MBGD）

每次迭代使用m个样本来对参数进行更新，公式：

${\mathbf{W}}_{t+1}={\mathbf{W}}_t-\eta \frac{1}{m}{\sum }_{k=i}^{i+m-1}\nabla J\left({\mathbf{W}}_t,X^{(k)},Y^{(k)}\right)$

梯度下降法优点：简单

缺点：训练速度慢，会进入局部极小值点，随机选择梯度的同时会引入噪声，使得权重更新的方向不一定正确

动量优化

SGD+Momentum

增加一个动量，使当前训练数据的梯度受到之前训练数据的影响。

$\{\begin{array}{l}{v}_t=\alpha v_{t-1}+{\eta }_t\nabla J\left(W_t,X^{\left(i_s\right)},Y^{\left(i_s\right)}\right)\\ W_{t+1}=W_t-v_t\end{array}$

加速收敛，有一定摆脱局部最优的能力

但仍具有SGD一部分的缺点

实际中可以尝试

NAG

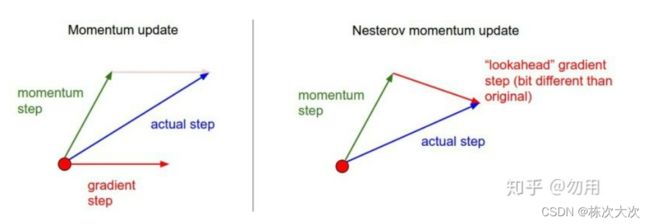
牛顿加速梯度动量优化方法(NAG, Nesterov accelerated gradient)：用上一步的速度先走一小步，再看当前的梯度然后再走一步，

$\{\begin{array}{l}{v}_t=\alpha v_{t-1}+{\eta }_t\Delta J\left(W_t-\alpha v_{t-1}\right)\\ W_{t+1}=W_t-v_t\end{array}$

https://zhuanlan.zhihu.com/p/62585696

可以理解为在标准动量中添加一个校正因子。

理解：在momentum中小球会盲目的跟从下坡的梯度，容易发生错误，所以需要一个更聪明的小球，能提前知道它要去哪，还有知道走到坡地的时候速度慢下来，而不是又崇尚另一坡。

优点：梯度下降的方向更加准确

缺点：对收敛率作用不是很大

pytorch中SGD:

模型每次反向传播都会给可学习参数p计算出一个偏导数$g_t$，用于更新对应的参数p。通常$g_t$不会直接作用到对应的可学习参数p上，而是通过优化器做一下处理，得到新的值${\hat{g}}_t$,即$F(g_t)$，然后和学习率lr一起用于更新参数

torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)

参数：

• params(iterable): iterable of parameters to optimize or dicts defining parameter groups

• lr(float): 学习率

• momentum (float, optional) : 动量因子 默认 0。通过上一次的v和当前的偏导数，得到本次的v。即：$v_t=v_{t-1}\ast momentum+g_t$, 这就是F。

  怎么理解：动量使得v具有惯性，这样可以缓和v的抖动，有时可以跳出局部极小。如：上次计算得到v=10，参数更新后本次的偏导是0，那么使用momentum=0.9后，最终用于更新可学习参数的v=9, 而不是0，这样参数仍会得到较大的更新，增加挑出局部极小值的可能性。

• dampening: 是乘到偏导g上的一个数，即：$v_t=v_{t-1}\ast momentum+g_t\ast (1-dampening)$，dampening在优化器第一次更新时不起作用。

• weight_decay (float, optional): 权重衰减 （L2 penalty）默认为0，即：L2 正则化，选择合适的权重衰减很重要，需要根据具体的情况取尝试，初步尝试可以选择 1e-4 或者 1e-3。

  作用于当前可学习参数p的值，即：$g_t=g_t+(p\ast weigh{t}_{d}ecay)$这里待更新的参数p的偏导就是$g_t$。

• nesterov (bool, optional): 当nesterov为True时，在上述$v_t$的基础上，最终得到$v_t=g_t+v_t\ast momentum$

  pytorch中SGD更新公式和其他框架略有不同。

  pytorch中是：v=m*v+g p=p-lr*v=p-lr*p*v-lr*g

  其他框架：v=m*v+lr*g p=p-v=p-m*v-lr*g

  动量的小知识：

  其物理意义和摩擦系数一致，有效抑制了速度，降低了系统的动能。通过交叉验证，这个参数通常设置为[0.5,0.9,0.95,0.99]中的一个。

  和学习率随着时间退火类似，momentum随时间变化的设置有时能略微改善效果，其中动量在学习过程的后阶段会上升。

  一个典型的设置是，刚开始将动量设为0.5，而在后面的多个周期中慢慢升到0.99.

自适应学习率

AdaGrad

AdaGrad算法通过记录历史梯度，能够随着训练过程自动减小学习率

${\theta }_t={\theta }_{t-1}-\frac{\eta }{\sqrt{{\sum }_{i=0}^{t-1}{\left(g_i\right)}^2}}{g}_{t-1}$

之前的方法是对所有的参数都是一个学习率，现在对不同的参数有不同的学习率。（接收到较大梯度值的权重更新的学习率将减小，而接收到较小梯度值的权重学习率将会变大）,适用于数据稀疏或者分布不平衡的数据集。

torch.optim.Adagrad(params,lr=0.01,lr_decay=0,weight_decay=0,initial_accumulator_value=0)

参数：

• params(iterable): 学习参数

• lr(float, optional) 学习率，默认0.01

• lr_decay(float, optional): 学习率衰减，默认0

• weight_decay(float, optional): L2惩罚系数 默认0

• initial_accumulator_value: 初始加速值，默认为0

优点：自动调整学习率

缺点：依赖一个人工设置的全局学习率，随着迭代次数增多，学习率会越来越小，最后趋于0（因为Adagrad累加之前所有梯度平方作为分母）

实际中不推荐

Adadelta

对Adagrad的改进，Adadelta分母中采用距离当前时间点比较近的累加项，这样可以避免训练后期，学习率过小。

torch.optim.Adadelta(params, lr=1.0,rho=0.9,eps=1e-6,weight_decay=0)

参数：

• params: 待优化的参数
• rho(float, optional) 用于计算平方梯度的运行平均值的系数 （默认0.9)
• eps(float, optional) 防止分母为0
• lr(float, optional) 学习率，默认为0
• weight_decay(float, optional) L2 默认为0

优点：避免后期，学习率过小，初期和中期，加速效果不错，训练速度快

缺点：还需要手动指定初始学习率，初始梯度很大的话，会导致整个训练过程学习率一直很小，在模型训练后期，模型会反复的在局部最小值附近抖动，从而导致学习时间变长。

RMSProp

Root Mean Square Prop，均方根传递

RMSProp简单修改了AdaGrad方法，它做了一个梯度平方的滑动平均。

${\theta }_t={\theta }_{t-1}-\frac{\eta }{\sqrt{v_t}}{g}_{t-1}$
$v_1=g_0^2$
$v_t=\alpha v_{t-1}+(1-\alpha ){\left(g_{t-1}\right)}^2$

通过累计各个变量的梯度的平法v，然后用每个变量的梯度除以v，即可有效缓解变量间的梯度差异。以下伪代码：

1. 初始化 x,y (假设只有两个学习参数)
2. 初始化学习率 lr
3. 初始化平滑常数（或者叫衰减速率）$\alpha$
4. 初始化 e 防止分母为0
5. 初始化，梯度的平方$v_x=0$, $v_y=0$ (有几个参数就有几个v)
6. while 没有停止训练 do
7. ​ 计算梯度 $g_x,g_y$
8. ​ 累计梯度的平方：$v_x=\alpha v_x+(1-\alpha )(g_x{)}^2$ （$v_y$ 同理)
9. ​ 更新可学习参数：$x=x-\frac{g_x}{\sqrt{v_x}+e}lr$ (y的更新同理)
10. end while

思想：梯度震动较大的项，在下降时，减小其下降速度，对于震动幅度较小的项，在下降时，加速其下降速度。采用均方根作为分母，可缓解Adagrad学习率下降较快的问题。

torch.optim.RMSProp(params,lr=0.01,alpha=0.99,eps=1e-8,weight_decay=0,momentum=0,centered=False)

参数：

• params (iterable): 待优化参数

• lr(float, optional) 学习率 默认0.01

• momentum (float, optional) 动量因子，默认0。

  在伪代码第8行，如果momentum=0，则继续后边的计算；

  否则计算过程变为：${\hat{v}}_x={\hat{v}}_x\ast momentum+\frac{g_x}{\sqrt{v_x}+e},x=x-{\hat{v}}_x\ast lr$, 其中${\hat{v}}_x$初始化为0，$g_x$是x的梯度，$v_x$是上述累计的x的梯度的平方。

• alpha (float, optional) 平滑常数，默认0.99

• eps (float, optional) 防止分母为0， 默认1e-8

• centered(bool, optional) 如果是false，按照伪代码计算

  如果为True，即：${\hat{g}}_x=\alpha {\hat{g}}_x+(1-\alpha )g_x,v_x=v_x-({\hat{g}}_x{)}^2$, 这里${\hat{g}}_x$初始化为0

  centered 和 RMSProp并无直接联系，是为了让结果更加平稳

• weight_decay (float, optional) L2惩罚 默认为0

优点：可缓解Adagrad学习率下降较快的问题，并且引入均方根，可减少摆动，对于RNN效果很好。

缺点：依然依赖全局学习率

推荐尝试，已经被证明是一种有效且实用的深度神经网络优化算法。

Adam

Adam看起来像是RMSProp的动量版本，做了两个改进：梯度滑动平均和偏差纠正。

梯度滑动平均

在RMSProp中，梯度的平方是通过平滑常数得到的，但并没有对梯度本身做平滑处理。在Adam中，对梯度也做了平滑处理，平滑后的滑动均值用m表示：即$m_t=\beta \ast m_{t-1}+(1-\beta )\ast g_t$

偏差纠正

上述m的滑动均值计算，当t=1，$m_1=\beta \ast m_0+(1-\beta )\ast g_1$，由于$m_0$初始为0，且$\beta$接近1，因此t较小时，m的值偏向于0，v也一样。这里通过除以$1-{\beta }^t$来进行偏差纠正，即${\hat{m}}_t=\frac{m_t}{1-{\beta }^t}$

伪代码：

初始lr, ${\beta }_1,{\beta }_2$分别用于平滑m和v，可学习参数${\theta }_0$, $m_0=0,v_0=0,t=0$

while 没有停止训练 do

​ 训练次数更新 t=t+1

​ 计算梯度：$g_t$ (所有学习参数都有自己的梯度，因此$g_t$表示的是全部梯度的集合)

​ 累计梯度：$m_t={\beta }_1\ast m_{t-1}+(1-{\beta }_1)\ast g_t$ (每个梯度对应一个m，m是一个集合)

​ 累计梯度的平方: $v_t={\beta }_2\ast v_{t-1}+(1-{\beta }_2)\ast (g_t{)}^2$ (v是一个集合)

​ 偏差纠正m：${\hat{m}}_t=\frac{m_t}{1-({\beta }_1{)}^t}$

​ 偏差纠正v: ${\hat{v}}_t=\frac{v_t}{1-({\beta }_2{)}^t}$

​ 更新参数：${\theta }_t={\theta }_{t-1}-\frac{{\hat{m}}_t}{\sqrt{{\hat{v}}_t}+e}lr$

将momentum算法和RMSProp算法结合起来使用的一种算法，既用动量来累积梯度，又使得收敛速度更快，同时使得波动的幅度更小，并进行了偏差修正。

torch.optim.Adam(params, lr=0.001, betas=(0.9,0.999),eps=1e-8,weight_decay=0,amsgrad=False)

参数：

• params

• lr (float, optional) 学习率 默认1e-3

• betas (Tuple[float, float], optional) 用于计算梯度以及梯度平法的滑动平均值的系数 （默认[0.9,0.99])

• eps (float, optional) 防止分母为0 默认1e-8

• weight_decay (float, optional) L2惩罚

• amsgrad(bool, optional) 是否使用amsgrad。如果为true，在上述伪代码基础上，保留历史最大的$v_t$, 记为$v_{max}$，每次计算都用最大的$v_{max}$，否则用当前$v_t$

优点：

1. 对目标函数没有平稳要求，即loss function可以随时间变化
2. 参数的更新不受梯度的伸缩变换影响
3. 更新步长和梯度大小无关，

性能比较

论文中的给出的结论，在训练数据上Adam比较好，在验证数据上SGDM表现比较好，一般选择Adam或者SGDM。或者在训练后期，使用SGDM。

常用SGDM，adam, RMSProp

warmup

学习率调整时模型训练中重要的参数之一，针对学习率的优化方法有很多种，warmup是重要的一种

什么是warmup

warmup是一种学习率优化方法，最早出现在resnet论文中，在模型训练初期选用较小的学习率，训练一段时间之后（10epoch 或者 10000steps）使用预设的学习率进行训练

为什么使用

1. 模型训练初期，权重随机化，对数据的理解为0，在第一个epoch中，模型会根据输入的数据进行快速的调参，此时如果采用较大的学习率，有很大的可能使模型学偏，后续需要更多的轮次才能拉回来
2. 当模型训练一段时间之后，对数据有一定的先验知识，此时使用较大的学习率模型不容易学偏，可以使用较大的学习率加速训练。
3. 当模型使用较大的学习率训练一段时间之后，模型的分布相对比较稳定，此时不宜从数据中再学到新的特点，如果继续使用较大的学习率会破坏模型的稳定性，而使用较小的学习率更获得最优。

实现：

wenet

class WarmupLR(_LRScheduler):
    """The WarmupLR scheduler

    This scheduler is almost same as NoamLR Scheduler except for following
    difference:

    NoamLR:
        lr = optimizer.lr * model_size ** -0.5
             * min(step ** -0.5, step * warmup_step ** -1.5)
    WarmupLR:
        lr = optimizer.lr * warmup_step ** 0.5
             * min(step ** -0.5, step * warmup_step ** -1.5)

    Note that the maximum lr equals to optimizer.lr in this scheduler.

    """
    def __init__(
        self,
        optimizer: torch.optim.Optimizer,
        warmup_steps: Union[int, float] = 25000,
        last_epoch: int = -1,
    ):
        assert check_argument_types()
        self.warmup_steps = warmup_steps

        # __init__() must be invoked before setting field
        # because step() is also invoked in __init__()
        super().__init__(optimizer, last_epoch)

    def __repr__(self):
        return f"{self.__class__.__name__}(warmup_steps={self.warmup_steps})"

    def get_lr(self):
        step_num = self.last_epoch + 1
        return [
            lr
            * self.warmup_steps ** 0.5
            * min(step_num ** -0.5, step_num * self.warmup_steps ** -1.5)
            for lr in self.base_lrs
        ]

    def set_step(self, step: int):
        self.last_epoch = step

欢迎关注个人公众号，分享知识和日常