LeetCode刷题day15

算法打卡第十五天,今天你刷题了吗


大家一起来刷题!

144. 二叉树的前序遍历

94. 二叉树的中序遍历

145. 二叉树的后序遍历

思路分析:

递归和迭代两种方法都可进行处理

方法一:递归

参考代码

//前序
void preorder(TreeNode* T) {
	if(T) {
		V.push_back(T->val);
		preorder(T->left);
		preorder(T->right);
	}
}
//中序
void inorder(TreeNode* T) {
	if(T) {	
		inorder(T->left);
		V.push_back(T->val);
		inorder(T->right);
	}
}
//后序
void postorder(TreeNode* T) {
	if(T) {
		postorder(T->left);
		postorder(T->right);
		V.push_back(T->val);
	}
}

vector<int> V;
vector<int> xxxorderTraversal(TreeNode* root) {
	xxxorder(root);
	return V;
}

方法二:迭代

本质上是在模拟递归，因为在递归的过程中使用了系统栈，所以在迭代的解法中常用Stack来模拟系统栈。

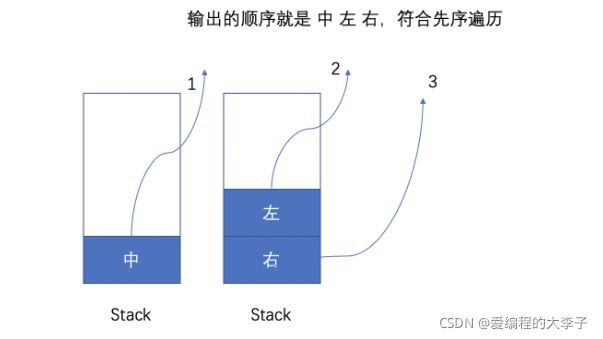
以前序遍历为例

• 首先我们应该创建一个Stack用来存放节点，首先我们想要打印根节点的数据，此时Stack里面的内容为空，所以我们优先将头结点加入Stack，然后打印。
• 之后我们应该先打印左子树，然后右子树。所以先加入Stack的就是右子树，然后左子树。

此时你能得到的流程如下:

参考代码2

//迭代做法. 
vector<int> preorderTraversal(TreeNode* root) {	
	if(root==null){
		return {};
	}
	vector<int> V;
	TreeNode* cur = root; 
	stack<TreeNode*> S;
	S.push(root); 	
	while(!stack.empty()){
		TreeNode* node = S.top();
		S.pop();
		V.push_back(node->val);//通过改变该语句的顺序,来决定是先序,中序和后序..
		if(node->right != NULL){
			S.push(node->right);
		} 
		if(node->left!=NULL){
			S.push(node->left);
		}
	}
	return V;
}

102. 二叉树的层序遍历

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

示例：

二叉树：[3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7
返回其层序遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

思路分析:

参考 BFS的使用场景总结

参考代码

#include
using namespace std;

https://leetcode-cn.com/problems/binary-tree-level-order-traversal/ 
struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode() : val(0), left(nullptr), right(nullptr) {}
	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
	TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

vector<vector<int>> levelOrder(TreeNode* root) {
	vector<vector<int>> V;
	queue<TreeNode*> Q;
	if(root==NULL){
		return {};
	}
	Q.push(root);
	while(!Q.empty()){
		int n  = Q.size();//计算当前层元素的个数 
		vector<int> v;
		for(int i = 0;i <n;i++){//将当前层元素弹出放到v中. 
			TreeNode* node = Q.front();
			Q.pop();
		
			v.push_back(node->val);
			if(node->left){
				Q.push(node->left);
			}
			if(node->right){
				Q.push(node->right);
			}			
		}
		V.push_back(v); 
	}
	return V;
}

104. 二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：

给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7
返回它的最大深度 3 。

参考代码

int maxDepth(TreeNode* root) {
	int m,n;
	if(root){
		return 0;
	}else{
		m = maxDepth(root->left);//递归计算左子树深度 
		n = maxDepth(root->right);//递归计算右子树深度 
		if(m>n){
			return m+1;//返回左右子树的最大值+1 
		}else{
			return n+1;
		}
	}

}

101. 对称二叉树

给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

   1
   / \
  2   2
 / \ / \
3  4 4  3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

    1
   / \
  2   2
   \   \
   3    3

方法一:递归

根据题目的描述，镜像对称，就是左右两边相等，也就是左子树和右子树是相当的。
注意这句话，左子树和右子相等，也就是说要递归的比较左子树和右子树。

• 我们将根节点的左子树记做 left，右子树记做 right。比较 left 是否等于 right，不等的话直接返回就可以了。
• 如果相当，比较 left 的左节点和 right 的右节点，再比较 left 的右节点和 right 的左节点

比如看下面这两个子树(他们分别是根节点的左子树和右子树)，能观察到这么一个规律：

• 左子树 2 的左孩子 == 右子树 2 的右孩子
• 左子树 2 的右孩子 == 右子树 2 的左孩子

   2         2
   / \       / \
  3   4     4   3
 / \ / \   / \ / \
8  7 6  5 5  6 7  8

根据上面信息可以总结出递归函数的两个条件：
终止条件：

• left 和 right 不等，或者 left 和 right 都为空
• 递归的比较 left.left 和 right.right，递归比较 left.right 和 right.left
  动态图如下:
  

时间复杂度:O(n)，因为要遍历 n 个节点
空间复杂度是 O(n),空间复杂度是递归的深度，也就是跟树高度有关，最坏情况下树变成一个链表结构，高度是n。

参考代码:

#include
using namespace std;
//https://leetcode-cn.com/problems/symmetric-tree/
struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode() : val(0), left(nullptr), right(nullptr) {}
	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
	TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
// 递归+dfs 
bool dfs(TreeNode* left,TreeNode* right){
	//递归终止的条件
	if(left==NULL&&right==NULL){
		return true;//肯定对称 
	} 
	if(left==NULL||right==NULL){
		return false;
	} 
	if(left->val!=right->val){
		return false;
	} 
	return dfs(left->left,right->right)&&dfs(left->right,right->left);
}

bool isSymmetric(TreeNode* root) {
	if(root==NULL){
		return true;
	}
	//调用递归函数,比较左节点和右节点
	return dfs(root->left,root->right); 
}





int main()
{
	return 0;
}

方法二:迭代

回想下递归的做法:
当两个子树的根节点相等时，就比较:左子树的 left 和 右子树的 right.
现在我们改用队列来实现，思路如下：

• 首先从队列中拿出两个节点(left 和 right)比较
• 将 left 的 left 节点和 right 的 right 节点放入队列
• 将 left 的 right 节点和 right 的 left 节点放入队列

时间复杂度是O(n)，空间复杂度是 O(n)

参考代码:

#include
using namespace std;
//https://leetcode-cn.com/problems/symmetric-tree/
struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode() : val(0), left(nullptr), right(nullptr) {}
	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
	TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
// 迭代 
bool isSymmetric(TreeNode* root) {
	if(root==NULL || (root->left==NULL && root->right==NULL)){
		return true;
	} 
	//用队列保存左右节点
	queue<TreeNode*> Q;
	Q.push(root->left);
	Q.push(root->right);
	while(!Q.empty()){
		TreeNode* left = Q.front();
		Q.pop();
		TreeNode *right = Q.front();
		Q.pop();
		if(left==NULL&&right==NULL){
//			return true;
			continue;//进行下一组节点的判断 
		}
		if(left==NULL||right==NULL){
			return false;
		}
		if(left->val!=right->val){
			return false;
		}
		//将左节点的左孩子,右节点的右孩子放入队列.
		Q.push(left->left);
		Q.push(right->right); 
		//将左节点的右孩子,右节点的左孩子放入队列 
		Q.push(left->right);
		Q.push(right->left);
	}
	return true;
}

大家卷起来!