哎呦-_-不错

数据预处理与特征工程—12.常见的数据预处理与特征工程手段总结

文章目录

- 引言
- 1.数据预处理
- - 1.1 数据清洗
  - - 1.1.1 异常值处理
    - 1.1.2 缺失值处理
  - 1.2 特征预处理
  - - 1.2.1 数值型特征无量纲化
    - 1.2.2 连续数值型特征分箱
    - - 1.2.2.1 无监督分箱法
      - 1.2.2.2 有监督分箱法
    - 1.2.3 统计变换
    - 1.2.4 类别特征编码
- 2.特征选择
- - 2.1 Filter(过滤式)
  - - 2.1.1 Pearson相关系数
    - 2.1.2 卡方验证
    - 2.1.3 互信息和最大信息系数
    - 2.1.4 距离相关系数
    - 2.1.5 方差选择法
  - 2.2 Wrapper(包裹式)
  - - 2.2.1 向前逐步选择
    - 2.2.2 向后逐步选择
    - 2.2.3 双向挑选
    - 2.2.4 递归特征消除法
  - 2.3 嵌入法
- 3.特征提取
- - 3.1 主成分分析PCA
  - 3.2 线性判别分析LDA
- 4.特征构造—创造新特征
- - 4.1. 数值特征的简单变换
  - 4.2 类别特征与数值特征的组合
  - 4.3 分组统计和基础特征工程方法结合
  - 4.3 笛卡尔乘积创造新特征
  - - 4.3.1 类别特征进行笛卡尔乘积特征组合
    - 4.3.2 连续特征与类别特征之间的笛卡尔乘积特征组合
    - 4.3.3 连续特征之间的笛卡尔乘积特征组合
  - 4.4 用基因编程创造新特征
  - 4.5 GBDT特征构造
  - 4.6 聚类特征构造
  - 4.7 日期/时间变量处理

引言

数据预处理与特征工程包括Data PreProcessing（数据预处理）、Feature Extraction（特征提取）、Feature Selection（特征选择）和Feature construction（特征构造）等步骤

1.数据预处理

数据预处理又包括数据清洗与特征预处理两步

1.1 数据清洗

数据清洗主要是删除原始数据集中的无关数据、重复数据，平滑噪声数据，筛选掉与挖掘主题无关的数据，处理缺失值、异常值等

1.1.1 异常值处理

异常值是否需要处理需要视具体情况而定，因为有些异常值可能蕴含着有用的信息。

简单统计量分析
在进行异常值分析时，可以先对变量做一个描述性统计，进而查看哪些数据是不合理的。最常用的统计量是最大值和最小值，用来判断这个变量的取值是否超出了合理范围。如客户年龄的最大值为199岁，则判断该变量的取值存在异常。

通过箱线图分析删除异常值；
箱型图提供了识别异常值的一个标准:异常值通常被定义为小于 $Q_L-1.5IQR$ 或大于 $Q_U+1.5IQR$ 的值。 $Q_L$ 称为下四分位数，表示全部观察值中有四分之一的数据取值比它小; $Q_U$ 称为上四分位数，表示全部观察值中有四分之一的数据取值比它大;IQR称为四分位数间距，是上四分位数 $Q_U$ 与下四分位数 $Q_L$ 之差，其间包含了全部观察值的一半。这里的1.5可以根据问题的不同进行改变。

箱型图依据实际数据绘制，对数据没有任何限制性要求，如服从某种特定的分布形式，它只是真实直观地表现数据分布的本来面貌;另一方面,箱型图判断异常值的标准以四分位数和四分位距为基础,四分位数具有一定的鲁棒性:多达25%的数据可以变得任意远而不会严重扰动四分位数,所以异常值不能对这个标准施加影响。由此可见,箱型图识别异常值的结果比较客观,在识别异常值方面有一定的优越性

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns


def box_plot_outliers(data_ser, box_scale):
    """
    利用箱线图去除异常值
    :param data_ser: 接收 pandas.Series 数据格式
    :param box_scale: 箱线图尺度，
    :return:
    """
    iqr = box_scale*(data_ser.quantile(0.75) - data_ser.quantile(0.25))
    # Q_L - 1.5IQR为下界
    val_low = data_ser.quantile(0.25) - iqr
    # Q_U + 1.5IQR为上界
    val_up = data_ser.quantile(0.75) + iqr
    rule_low = (data_ser < val_low)
    rule_up = (data_ser > val_up)
    return (rule_low, rule_up), (val_low, val_up)

def outliers_proc(data, col_name, scale=1.5):
    """
    用于清洗异常值，默认用 box_plot（scale=1.5）进行清洗
    :param data: 接收 pandas 数据格式
    :param col_name: pandas 列名
    :param scale: 尺度
    :return:
    """
    # 复制数据
    data_n = data.copy()
    # 针对哪一个特征清洗异常值
    data_series = data_n[col_name]
    # 返回异常值索引(bool格式)与上下边界
    rule, value = box_plot_outliers(data_series, box_scale=scale)
    # 得到异常值得索引
    # |会先转化成二进制，然后相同位数的数字有1则为1，否则为0
    index = np.arange(data_series.shape[0])[rule[0] | rule[1]]
    print("Delete number is: {}".format(len(index)))

    # 删除异常值
    data_n = data_n.drop(index)
    # 重置索引
    data_n.reset_index(drop=True, inplace=True)
    print("Now column number is: {}".format(data_n.shape[0]))
    # 统计低于下界的异常值
    index_low = np.arange(data_series.shape[0])[rule[0]]
    outliers = data_series.iloc[index_low]
    print("Description of data less than the lower bound is:")
    print(pd.Series(outliers).describe())

    # 统计高于上界的异常值
    index_up = np.arange(data_series.shape[0])[rule[1]]
    outliers = data_series.iloc[index_up]
    print("Description of data larger than the upper bound is:")
    print(pd.Series(outliers).describe())

    # 查看删除异常值前后图形的区别
    fig, ax = plt.subplots(1, 2, figsize=(10, 7))
    sns.boxplot(y=data[col_name], data=data, palette="Set1", ax=ax[0])
    sns.boxplot(y=data_n[col_name], data=data_n, palette="Set1", ax=ax[1])
    return data_n

通过 $3 σ$ 原则删除异常值

如果数据服从正态分布，在 $3 σ$ 原则下，异常值被定义为一组测定值中与平均值的偏差超过3倍标准差的值。在正态分布的假设下，距离平均值 $3 σ$ 之外的值出现的概率为P(x-u |> $3 σ$ )≤0.003，属于极个别的小概率事件。
如果数据不服从正态分布，也可以用远离平均值的标准差倍数来描述。
长尾截断；

长尾截断主要也是分布不符合正态分布，而是类似于“长尾”。例如房价中，低价占大部分，豪宅属于小部分。应对这种数据分布，一般可以通过神奇的log化处理转化类近似正态分布或者使用Box-Cox转换将数据转换为正态。数据预处理—5.box-cox变换及python实现
将异常值视为缺失值，利用缺失处理方法进行处理

1.1.2 缺失值处理

缺失值处理的方法可分为3种：删除记录、数据插补和不处理

不处理（针对类似 XGBoost 等树模型）；
删除（缺失数据太多）；
插值补全，包括均值/中位数/众数/使用固定值/最近邻插补/回归方法/插值法(拉格朗日插值法、牛顿插值法)等；
前面几种方面使用pandas中的fillna函数可以轻松实现
插值法：数据预处理—7.数据插补之拉格朗日插值法、牛顿差值法及python实现
回归方法：对带有缺失值的变量，根据已有数据和其有关的其他变量(因变量)的数据建立拟合模型来预测缺失的属性值。6.4 随机森林实战这里面使用了随机森林来预测年龄中的缺失值作为填充
分箱，缺失值一个箱；
见后面

1.2 特征预处理

1.2.1 数值型特征无量纲化

数值型特征无量纲化是为了消除样本不同属性具有不同量级（大小）时的影响，不仅提高精度，而且提高迭代精度

标准化（转换为标准正态分布）；
```
from sklearn.preprocessing import MinMaxScaler,StandardScaler
# 标准化
scaler = StandardScaler()
result = scaler.fit_transform(data)  # 将data标准化

scaler.inverse_transform(result)  # 将标准化结果逆转
```
优点：
标准化最大的优点就是简单，容易计算，Z-Score能够应用于数值型的数据，并且不受数据量级（数据多少）的影响，因为它本身的作用就是消除量级给分析带来的不便。
缺点：
- 估算Z-Score需要总体的平均值与方差，但是这一值在真实的分析与挖掘中很难得到，大多数情况下是用样本的均值与标准差替代。
- Z-Score对于数据的分布有一定的要求，正态分布是最有利于Z-Score计算的。
- Z-Score消除了数据具有的实际意义，属性A的Z-Score与属性B的Z-Score与他们各自的分数不再有关系，因此Z-Score的结果只能用于比较数据间的结果，数据的真实意义还需要还原原值。
- 在存在异常值时无法保证平衡的特征尺度。

归一化（转换到 [0,1] 区间）；

from sklearn.preprocessing import MinMaxScaler,StandardScaler
# 归一化
scaler = MinMaxScaler()
result = scaler.fit_transform(data)  # 将data归一化

scaler.inverse_transform(result) # 将归一化结果逆转

缺点：

这种方法有一个缺陷就是当有新数据加入时，可能导致max和min的变化，需要重新定义。
MinMaxScaler对异常值的存在非常敏感。

MaxAbs归一化
定义：单独地缩放和转换每个特征，使得训练集中的每个特征的最大绝对值将为1.0，将属性缩放到[-1,1]。它不会移动/居中数据，因此不会破坏任何稀疏性。
```
from sklearn.preprocessing import MaxAbsScaler
maxAbsScaler = MaxAbsScaler().fit(X_train) 
maxAbsScaler.transform(X_train)
```
缺点：
1. 这种方法有一个缺陷就是当有新数据加入时，可能导致max和min的变化，需要重新定义；
2. 对异常值的存在非常敏感
正态分布化（Normalization）
定义：正则化的过程是将每个样本缩放到单位范数(每个样本的范数为1)。Normalization主要思想是对每个样本计算其p-范数，然后对该样本中每个元素除以该范数，这样处理的结果是使得每个处理后样本的p-范数(l1-norm,l2-norm)等于1。

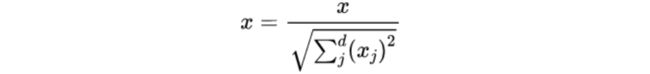
适用情形：如果要使用如二次型(点积)或者其它核方法计算两个样本之间的相似性这个方法会很有用。该方法是文本分类和聚类分析中经常使用的向量空间模型（Vector Space Model)的基础。
```
from sklearn.preprocessing import Normalizer
#正态归一化，返回值为正态归一化后的数据 
normalizer = Normalizer(norm='l2').fit(X_train) 
normalizer.transform(X_train)
```
针对幂律分布，可以采用公式： $log\frac{1+x}{1+median}$

1.2.2 连续数值型特征分箱

一些数据挖掘算法，特别是某些分类算法，如ID3算法、Apriori算法等，要求数据是分类属性形式。这样，常常需要将连续属性变换成分类属性，即连续属性离散化。
连续属性离散化的优势：

离散后稀疏向量内积乘法运算速度更快，计算结果也方便存储，容易扩展；

离散后的特征对异常值更具鲁棒性，如 age>30 为 1 否则为 0，对于年龄为 200 的也不会对模型造成很大的干扰；

LR 属于广义线性模型，表达能力有限，经过离散化后，每个变量有单独的权重，这相当于引入了非线性，能够提升模型的表达能力，加大拟合；

离散后特征可以进行特征交叉，提升表达能力，由 M+N 个变量编程 M*N 个变量，进一步引入非线形，提升了表达能力；

特征离散后模型更稳定，如用户年龄区间，不会因为用户年龄长了一岁就变化

连续属性离散化就是在数据的取值范围内设定若干个离散的划分点，将取值范围划分为一些离散化的区间，最后用不同的符号或整数值代表落在每个子区间中的数据值。所以，连续属性离散化涉及两个子任务:确定分类数以及如何将连续属性值映射到这些分类值。特征分箱可分为无监督分箱与有监督分箱方法。

1.2.2.1 无监督分箱法

自定义分箱
定义：自定义分箱，是根据业务经验或者常识等自行设定划分的区间，然后将原始数据归类到各个区间中。

等距分箱
将属性的值域分成具有相同宽度的区间，区间的个数由数据本身的特点决定或者用户指定。等距分箱只考虑区间宽度相同，每个区间里面的实例数量可能不等。

	import pandas as pd
import numpy as np

df = pd.DataFrame([[22, 1], [13, 1], [33, 1],
                   [52, 0], [16, 0], [42, 1], [53, 1], [39, 1], [26, 0], [66, 0]], columns=['age', 'Y'])
k = 4
# 等宽离散化，各个类别依次命名为0,1,2,3
df['age_bin'] = pd.cut(df['age'], k)
df['age_bin_label'] = pd.cut(df['age'], k, labels=range(k))
print(df)

   age  Y          age_bin age_bin_label
0   22  1  (12.947, 26.25]             0
1   13  1  (12.947, 26.25]             0
2   33  1    (26.25, 39.5]             1
3   52  0    (39.5, 52.75]             2
4   16  0  (12.947, 26.25]             0
5   42  1    (39.5, 52.75]             2
6   53  1    (52.75, 66.0]             3
7   39  1    (26.25, 39.5]             1
8   26  0  (12.947, 26.25]             0
9   66  0    (52.75, 66.0]             3

缺点：一方面需要人为规定划分的区间个数，另一方面，它对离群点比较敏感，倾向于不均匀地把属性值分布到各个区间。有些区间包含许多数据，而另外一些区间的数据极少，这样会严重损坏建立的决策模型。

等频分箱；
将相同数量的记录放进每个区间。

import pandas as pd
import numpy as np

df = pd.DataFrame([[22, 1], [13, 1], [33, 1],
                   [52, 0], [16, 0], [42, 1], [53, 1], [39, 1], [26, 0], [66, 0]], columns=['age', 'Y'])
k = 5
# 等频离散化，各个类别依次命名为0,1,2,3，4
df['age_bin'] = pd.qcut(df['age'], k)
df['age_bin_label'] = pd.qcut(df['age'], k, labels=range(k))
print(df)

   age  Y         age_bin age_bin_label
0   22  1    (20.8, 30.2]             1
1   13  1  (12.999, 20.8]             0
2   33  1    (30.2, 40.2]             2
3   52  0    (40.2, 52.2]             3
4   16  0  (12.999, 20.8]             0
5   42  1    (40.2, 52.2]             3
6   53  1    (52.2, 66.0]             4
7   39  1    (30.2, 40.2]             2
8   26  0    (20.8, 30.2]             1
9   66  0    (52.2, 66.0]             4

缺点：
等频法虽然避免了等距分箱问题的产生，却可能将相同的数据值分到不同的区间，以满足每个区间中固定的数据个数。

基于聚类分箱
定义：基于k均值聚类的分箱方法，k均值聚类法将观测值聚为k类，但在聚类过程中需要保证分箱的有序性，第一个分箱中所有观测值都要小于第二个分箱中的观测值，第二个分箱中所有观测值都要小于第三个分箱中的观测值，以此类推。
聚类分箱具体步骤：

对预处理后的数据进行归一化处理。
将归一化处理过的数据，应用k-means聚类算法，划分为多个区间：采用等距法设定k-means聚类算法的初始中心，得到聚类中心。
在得到聚类中心后将相邻的聚类中心的中点作为分类的划分点，将各个对象加入到距离最近的类中，从而将数据划分为多个区间。
重新计算每个聚类中心，然后重新划分数据，直到每个聚类中心不再变化，得到最终的聚类结果。

import pandas as pd
import numpy as np
from sklearn.cluster import KMeans

k = 4
df = pd.DataFrame([[22, 1], [13, 1], [33, 1],
                   [52, 0], [16, 0], [42, 1], [53, 1], [39, 1], [26, 0], [66, 0]],
                  columns=['age', 'Y'])
# k为聚成几类
kmodel = KMeans(n_clusters=k)
# 训练模型
kmodel.fit(df['age'].values.reshape(len(df), 1))
# 求聚类中心
c = pd.DataFrame(kmodel.cluster_centers_,columns=['聚类中心'])
# 排序　　
c = c.sort_values(by='聚类中心')
# 用滑动窗口求均值的方法求相邻两项求中点，作为边界点
w = c.rolling(window=2).mean().iloc[1:]
# 把首末边界点加上
w = [0] + list(w['聚类中心'].values) +[df['age'].max()]
#
df['age_bins'] = pd.cut(df['age'], w)
df['age_bins_label'] = pd.cut(df['age'], w, labels=range(k))
print(df)

   age  Y         age_bins age_bins_label
0   22  1    (0.0, 28.625]              0
1   13  1    (0.0, 28.625]              0
2   33  1  (28.625, 45.25]              1
3   52  0   (45.25, 59.25]              2
4   16  0    (0.0, 28.625]              0
5   42  1  (28.625, 45.25]              1
6   53  1   (45.25, 59.25]              2
7   39  1  (28.625, 45.25]              1
8   26  0    (0.0, 28.625]              0
9   66  0    (59.25, 66.0]              3

二值化分箱
定义：二值化可以将数值型（numerical）的特征进行阀值化得到boolean型数据。这对于下游的概率估计来说可能很有用（比如：数据分布为Bernoulli分布时）。定量特征二值化的核心在于设定一个阈值，大于阈值的赋值为1，小于等于阈值的赋值为0。
```
from sklearn.preprocessing import Binarizer  
# Binarizer函数也可以设定一个阈值，结果数据值大于阈值的为1，小于阈值的为0 
binarizer = Binarizer(threshold=0.0).fit(X_train) 
binarizer.transform(X_train)
```

1.2.2.2 有监督分箱法

卡方分箱
定义：自底向上的(即基于合并的)数据离散化方法。它依赖于卡方检验：具有最小卡方值的相邻区间合并在一起,直到满足确定的停止准则。
基本思想：对于精确的离散化，相对类频率在一个区间内应当完全一致。因此,如果两个相邻的区间具有非常类似的类分布，则这两个区间可以合并，否则，它们应当保持分开（组内的差别很小，组间的差别很大）。而低卡方值表明它们具有相似的类分布。
卡方分箱的具体步骤：

连续变量的卡方分箱，返回分箱点，下面是在申请评分卡中，进行卡方分箱的函数

def AssignGroup(x, bin):
    """
    将超过100个的属性值调整到100个
    :param x: 属性值
    :param bin: 99个分割点
    :return: 调整后的值
    """
    N = len(bin)
    if x <= min(bin):
        return min(bin)
    elif x > max(bin):
        return 10e10
    else:
        for i in range(N - 1):
            if bin[i] < x <= bin[i + 1]:
                return bin[i + 1]
 def Chi2(df, total_col, bad_col, overallRate):
    '''
    # 计算卡方值
    :param df: the dataset containing the total count and bad count
    :param total_col: total count of each value in the variable
    :param bad_col: bad count of each value in the variable
    :param overallRate: the overall bad rate of the training set—逾期率
    :return: the chi-square value
    '''
    df2 = df.copy()
    df2['expected'] = df[total_col].apply(lambda x: x * overallRate)
    combined = zip(df2['expected'], df2[bad_col])
    chi = [(i[0] - i[1]) ** 2 / i[0] for i in combined]
    chi2 = sum(chi)
    return chi2

def ChiMerge_MaxInterval(df, col, target, max_interval=5):
    '''
    通过指定最大分箱数，使用卡方值拆分连续变量
    :param df: the dataframe containing splitted column, and target column with 1-0
    :param col: splitted column
    :param target: target column with 1-0
    :param max_interval: 最大分箱数
    :return: 返回分箱点
    '''
    colLevels = sorted(list(set(df[col])))
    N_distinct = len(colLevels)
    if N_distinct <= max_interval:
        print("The number of original levels for {} is less than or equal to max intervals".format(col))
        return colLevels[:-1]
    else:
        # 如果属性过多，则时间代价较大，不妨取100个属性进行分箱
        if N_distinct > 100:
            ind_x = [int(i / 100.0 * N_distinct) for i in range(1, 100)]
            split_x = [colLevels[i] for i in ind_x]
            # 超过100个属性值调整为100个
            df['temp'] = df[col].map(lambda x: AssignGroup(x, split_x))
        else:
            df['temp'] = df[col]
        # Step 1: group the dataset by col and work out the total count & bad count in each level of the raw column
        # 按col对数据集进行分组，并计算出total count & bad count
        total = df.groupby(['temp'])[target].count()
        total = pd.DataFrame({'total': total})
        bad = df.groupby(['temp'])[target].sum()
        bad = pd.DataFrame({'bad': bad})
        regroup = total.merge(bad, left_index=True, right_index=True, how='left')
        regroup.reset_index(level=0, inplace=True)
        N = sum(regroup['total'])
        B = sum(regroup['bad'])
        # the overall bad rate will be used in calculating expected bad count
        # 计算总的逾期率
        overallRate = B * 1.0 / N
        # initially, each single attribute forms a single interval
        # since we always combined the neighbours of intervals, we need to sort the attributes
        colLevels = sorted(list(set(df['temp'])))
        groupIntervals = [[i] for i in colLevels]
        groupNum = len(groupIntervals)
        # 终止条件：在迭代的每个步骤中，间隔数等于预先指定的阈值（最大分箱数），我们计算每个属性的卡方值
        while (len(groupIntervals) > max_interval):
            chisqList = []
            for interval in groupIntervals:
                df2 = regroup.loc[regroup['temp'].isin(interval)]
                chisq = Chi2(df2, 'total', 'bad', overallRate)
                chisqList.append(chisq)
            # 找到最小卡方值的位置，并将该卡方值与左右两侧相邻的较小的卡方值合并
            min_position = chisqList.index(min(chisqList))
            if min_position == 0:
                combinedPosition = 1
            elif min_position == groupNum - 1:
                combinedPosition = min_position - 1
            else:
                if chisqList[min_position - 1] <= chisqList[min_position + 1]:
                    combinedPosition = min_position - 1
                else:
                    combinedPosition = min_position + 1
            groupIntervals[min_position] = groupIntervals[min_position] + groupIntervals[combinedPosition]
            # after combining two intervals, we need to remove one of them
            groupIntervals.remove(groupIntervals[combinedPosition])
            groupNum = len(groupIntervals)
        groupIntervals = [sorted(i) for i in groupIntervals]
        # 取最大的点
        cutOffPoints = [i[-1] for i in groupIntervals[:-1]]
        del df['temp']
        return cutOffPoints

或者参考这个创建卡方分箱脚本

Best-KS 分箱（类似利用基尼指数进行二分类）；

下面是KS值计算公式介绍：

def calc_ks(count, idx):
    """
    计算各分组的KS值
    :param count: DataFrame 待分箱变量各取值的正负样本数
    :param group: list 单个分组信息
    :return: 该分箱的ks值

    计算公式：KS_i = |sum_i / sum_T - (size_i - sum_i)/ (size_T - sum_T)|
    """
    # 计算每个评分区间的好坏账户数。
    # 计算各每个评分区间的累计好账户数占总好账户数比率（good %)和累计坏账户数占总坏账户数比率（bad %）。
    # 计算每个评分区间累计坏账户比与累计好账户占比差的绝对值（累计good % -累计bad %），然后对这些绝对值取最大值记得到KS值
    ks = 0.0
    # 计算全体样本中好坏样本的比重(左开右闭区间)
    good = count[1].iloc[0:idx + 1].sum() / count[1].sum() if count[1].sum()!=0 else 1
    bad = count[0].iloc[0:idx + 1].sum() / count[0].sum() if count[0].sum()!=0 else 1
    ks += abs(good - bad)
    
    good = count[1].iloc[idx + 1:].sum() / count[1].sum() if count[1].sum()!=0 else 1
    bad = count[0].iloc[idx + 1:].sum() / count[0].sum() if count[0].sum()!=0 else 1
    ks += abs(good - bad)
    return ks

或者参考特征工程之分箱–Best-KS分箱
3. 决策树分箱；
决策树分箱步骤为：

利用sklearn决策树，DecisionTreeClassifier的.tree_属性获得决策树的节点划分值；
基于上述得到的划分值，利用pandas.cut函数对变量进行分箱；
计算各个分箱的WOE、IV值。
具体可参考这篇博客基于sklearn决策树的最优分箱与IV值计算-Python实现

1.2.3 统计变换

统计变换的主要作用在于它能帮助稳定方差，始终保持分布接近于正态分布并使得数据与分布的平均值无关。
数据右偏的话可以对所有数据取对数、取平方根等，它的原理是因为这样的变换的导数是逐渐减小的，也就是说它的增速逐渐减缓，所以就可以把大的数据向左移，使数据接近正态分布。如果左偏的话可以取相反数转化为右偏的情况。
通常来说，可以尝试一下几种方法：
如果数据高度偏态，则使用对数变换

对数变换即将原始数据X的对数值作为新的分布数据：
```
x = np.log(x)
```
当原始数据中有小值及零时, $log{(1+x)}$
```
x = np.log1p(x)
```

如果数据轻度偏态，则使用平方根变换

平方根变换即将原始数据X的平方根作为新的分布数据
```
x = np.sqrt(x)
```

如果数据的两端波动较大，则使用倒数变换

倒数变换即将原始数据X的倒数作为新的分析数据
```
x = 1 / x
```

box-cox变换
定义：Box-Cox 变换是另一种流行的幂变换函数簇中的一个函数。该函数有一个前提条件，即数值型数值必须先变换为正数（与 log 变换所要求的一样）。如果数值是负的，可以利用常数对数值进行偏移。

## Import necessary modules 
from scipy.special import boxcox1p
from scipy.stats import boxcox_normmax

def fixing_skewness(df):
    """
    This function takes in a dataframe and return fixed skewed dataframe
    """
    # 得到所有非类别型变量
    numeric_feats = df.dtypes[df.dtypes != "object"].index

    # 计算所有非类别型特征的偏态并排序
    skewed_feats = df[numeric_feats].apply(lambda x: x.skew()).sort_values(ascending=False)
    # 对偏态大于0.5的进行修正，大于0是右偏，小于0是左偏
    high_skew = skewed_feats[abs(skewed_feats) > 0.5]
    skewed_features = high_skew.index

    # 修正
    for feat in skewed_features:
    	# 这里是+1是保证数据非负，否则会弹出错误，没有其他含义，不会影响对偏态的修正
        df[feat] = boxcox1p(df[feat], boxcox_normmax(df[feat] + 1))

1.2.4 类别特征编码

标签编码（LabelEncode）
定义：LabelEncoder是对不连续的数字或者文本进行编号，编码值介于0和n_classes-1之间的标签。
优点：相对于OneHot编码，LabelEncoder编码占用内存空间小，并且支持文本特征编码。
缺点：它隐含了一个假设：不同的类别之间，存在一种顺序关系。在具体的代码实现里，LabelEncoder会对定性特征列中的所有独特数据进行一次排序，从而得出从原始输入到整数的映射。应用较少，一般在树模型中可以使用。
```
from sklearn.preprocessing import LabelEncoder 
le = LabelEncoder() 
le.fit(["paris", "paris", "tokyo", "amsterdam"])  
print('特征：{}'.format(list(le.classes_)))  
# 输出 特征：['amsterdam', 'paris', 'tokyo']  
print('转换标签值：{}'.format(le.transform(["tokyo", "tokyo", "paris"])))  
# 输出 转换标签值：array([2, 2, 1]...)  
print('特征标签值反转：{}'.format(list(le.inverse_transform([2, 2, 1]))))  
# 输出 特征标签值反转：['tokyo', 'tokyo', 'paris']
```
独热编码（OneHotEncode）

为什么要使用独热编码？
独热编码是因为大部分算法是基于向量空间中的度量来进行计算的，为了使非偏序关系的变量取值不具有偏序性，并且到圆点是等距的。使用one-hot编码，将离散特征的取值扩展到了欧式空间，离散特征的某个取值就对应欧式空间的某个点。将离散型特征使用one-hot编码，会让特征之间的距离计算更加合理。

为什么特征向量要映射到欧式空间？
将离散特征通过one-hot编码映射到欧式空间，是因为，在回归、分类、聚类等机器学习算法中，特征之间距离的计算或相似度的计算是非常重要的，而我们常用的距离或相似度的计算都是在欧式空间的相似度计算。

优点：独热编码解决了分类器不好处理属性数据的问题，在一定程度上也起到了扩充特征的作用。它的值只有0和1，不同的类型存储在垂直的空间。
缺点：当类别的数量很多时，特征空间会变得非常大。在这种情况下，一般可以用PCA来减少维度。而且one hot encoding+PCA这种组合在实际中也非常有用。
```
from sklearn.preprocessing import OneHotEncoder  
enc = OneHotEncoder() 
enc.fit([[0, 0, 3], [1, 1, 0], [0, 2, 1], [1, 0, 2]])    
# fit来学习编码 
enc.transform([[0, 1, 3]]).toarray()    
# 进行编码  
# 输出：array([[ 1., 0., 0., 1., 0., 0., 0., 0., 1.]])
```

标签二值化（LabelBinarizer）
定义：功能与OneHotEncoder一样，但是OneHotEncode只能对数值型变量二值化，无法直接对字符串型的类别变量编码，而LabelBinarizer可以直接对字符型变量二值化。

from sklearn.preprocessing import LabelBinarizer  
lb = LabelBinarizer() 
lb.fit([1, 2, 6, 4, 2])  
print(lb.classes_) 
# 输出 array([1, 2, 4, 6])  
print(lb.transform([1, 6])) 
# 输出 array([[1, 0, 0, 0],
              [0, 0, 0, 1]])  
print(lb.fit_transform(['yes', 'no', 'no', 'yes'])) 
# 输出 array([[1],
              [0],
              [0],
              [1]])

多标签二值化（MultiLabelBinarizer）
定义：用于label encoding，生成一个(n_examples * n_classes)大小的0~1矩阵，每个样本可能对应多个label。
适用情形：

每个特征中有多个文本单词。
用户兴趣特征（如特征值：”健身电影音乐”）适合使用多标签二值化，因为每个用户可以同时存在多种兴趣爱好。
多分类类别值编码的情况。
电影分类标签中（如：[action, horror]和[romance, commedy]）需要先进行多标签二值化，然后使用二值化后的值作为训练数据的标签值。
```
from sklearn.preprocessing import MultiLabelBinarizer  
mlb = MultiLabelBinarizer()  
print(mlb.fit_transform([(1, 2), (3,)]))  
# 输出 array([[1, 1, 0]，
        [0, 0, 1]])  
print(mlb.classes_)  
# 输出：array([1, 2, 3])  
print(mlb.fit_transform([{'sci-fi', 'thriller'}, {'comedy'}]))  
# 输出：array([[0, 1, 1],
        [1, 0, 0]])  
print(list(mlb.classes_))  
# 输出：['comedy', 'sci-fi', 'thriller']
```
平均数编码（Mean Encoding）
定义：平均数编码（mean encoding）的编码方法，在贝叶斯的架构下，利用所要预测的因变量（target variable），有监督地确定最适合这个定性特征的编码方式。
适用情形：平均数编码（mean encoding），针对高基数类别特征的有监督编码。当一个类别特征列包括了极多不同类别时（如家庭地址，动辄上万）时，可以采用。
高基数定性特征的例子：IP地址、电子邮件域名、城市名、家庭住址、街道、产品号码。
为什么要用平均数编码？
- 如果某一个特征是定性的（categorical），而这个特征的可能值非常多（高基数），那么平均数编码（mean encoding）是一种高效的编码方式。在实际应用中，这类特征工程能极大提升模型的性能。
- 因为定性特征表示某个数据属于一个特定的类别，所以在数值上，定性特征值通常是从0到n的离散整数。例子：花瓣的颜色（红、黄、蓝）、性别（男、女）、地址、某一列特征是否存在缺失值（这种NA 指示列常常会提供有效的额外信息）。
- 一般情况下，针对定性特征，我们只需要使用sklearn的OneHotEncoder或LabelEncoder进行编码，这类简单的预处理能够满足大多数数据挖掘算法的需求。定性特征的基数（cardinality）指的是这个定性特征所有可能的不同值的数量。在高基数（high cardinality）的定性特征面前，这些数据预处理的方法往往得不到令人满意的结果。
优点：和独热编码相比，节省内存、减少算法计算时间、有效增强模型表现。
代码部分参考：平均数编码：针对高基数定性特征（类别特征）的数据预处理/特征工程

2.特征选择

特征选择的目标是寻找最优特征子集。特征选择能剔除不相关(irrelevant)或冗余(redundant )的特征，从而达到减少特征个数，提高模型精确度，减少运行时间的目的。另一方面，选取出真正相关的特征简化模型，协助理解数据产生的过程。
特征选择的一般过程如下：

生成子集：搜索特征子集，为评价函数提供特征子集
评价函数：评价特征子集的好坏
停止准则：与评价函数相关，一般是阈值，评价函数达到一定标准后就可停止搜索
验证过程：在验证数据集上验证选出来的特征子集的有效性

根据特征选择的形式，可分为三大类：

Filter(过滤式)：按照发散性或相关性对各个特征进行评分，设定阈值或者待选择特征的个数进行筛选
Wrapper(包裹式)：根据目标函数（往往是预测效果评分），每次选择若干特征，或者排除若干特征
Embedded(嵌入式)：先使用某些机器学习的模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征（类似于Filter，只不过系数是通过训练得来的）

2.1 Filter(过滤式)

过滤式的基本想法是：分别对每个特征 $x_i$ ，计算 $x_i$ 相对于类别标签 $y$ 的信息量 $S (i)$ ，得到 $n$ 个结果。然后将 $n$ 个 $S (i)$ 按照从大到小排序，输出前 $k$ 个特征。显然，这样复杂度大大降低。那么关键的问题就是使用什么样的方法来度量 $S (i)$ ，我们的目标是选取与 $y$ 关联最密切的一些特征 $x_i$ 。
下面介绍一些指标：

Pearson相关系数
卡方验证
互信息和最大信息系数
距离相关系数
方差选择法

2.1.1 Pearson相关系数

皮尔森相关系数是一种最简单的，能帮助理解特征和响应变量之间关系的方法，衡量的是变量之间的线性相关性，结果的取值区间为[-1,1] ， -1 表示完全的负相关(这个变量下降，那个就会上升)， +1 表示完全的正相关， 0 表示没有线性相关性。Scipy的pearsonr方法能够同时计算相关系数和p-value。

import numpy as np
from scipy.stats import pearsonr

np.random.seed(0)
size = 300
x = np.random.normal(0, 1, size)
print("Lower noise：", pearsonr(x, x + np.random.normal(0, 1, size)))
print("Higher noise：", pearsonr(x, x + np.random.normal(0, 10, size)))


from sklearn.feature_selection import SelectKBest
# 选择K个最好的特征，返回选择特征后的数据
# 第一个参数为计算评估特征是否好的函数，该函数输入特征矩阵和目标向量，输出二元组（评分，P值）的数组，数组第i项为第i个特征的评分和P值。在此定义为计算相关系数
# 参数k为选择的特征个数
SelectKBest(lambda X, Y: array(map(lambda x:pearsonr(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)

Pearson相关系数的一个明显缺陷是：作为特征排序机制，他只对线性关系敏感。如果关系是非线性的，即便两个变量具有一一对应的关系，Pearson相关性也可能会接近 0 。

2.1.2 卡方验证

经典的卡方检验是检验类别型变量对类别型变量的相关性。假设自变量有N种取值，因变量有M种取值，考虑自变量等于i且因变量等于j的样本频数的观察值与期望的差距，构建统计量：

不难发现，这个统计量的含义简而言之就是自变量对因变量的相关性。用sklearn中feature_selection库的SelectKBest类结合卡方检验来选择特征的代码如下：

from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
iris = load_iris()
X, y = iris.data, iris.target  #iris数据集

#选择K个最好的特征，返回选择特征后的数据
X_new = SelectKBest(chi2, k=2).fit_transform(X, y)

sklearn.feature_selection模块中的类可以用于样本集中的特征选择/维数降低，以提高估计器的准确度分数或提高其在非常高维数据集上的性能。

2.1.3 互信息和最大信息系数

经典的互信息也是评价类别型变量对类别型变量的相关性的，互信息公式如下：

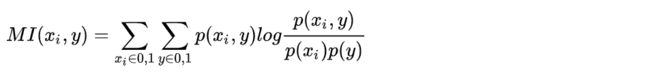
互信息直接用于特征选择其实不是太方便：

它不属于度量方式，也没有办法归一化，在不同数据及上的结果无法做比较
对于连续变量的计算不是很方便（ X 和 Y 都是集合, x_i, y 都是离散的取值），通常变量需要先离散化，而互信息的结果对离散化的方式很敏感

最大信息系数克服了这两个问题。它首先寻找一种最优的离散化方式，然后把互信息取值转换成一种度量方式，取值区间在 [0,1] 。minepy提供了MIC功能。

from minepy import MINE

m = MINE()
x = np.random.uniform(-1, 1, 10000)
m.compute_score(x, x**2)
print(m.mic())


from sklearn.feature_selection import SelectKBest
#由于MINE的设计不是函数式的，定义mic方法将其为函数式的，返回一个二元组，二元组的第2项设置成固定的P值0.5
def mic(x, y):
    m = MINE()
    m.compute_score(x, y)
    return (m.mic(), 0.5)
# 选择K个最好的特征，返回特征选择后的数据
SelectKBest(lambda X, Y: array(map(lambda x:mic(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)

2.1.4 距离相关系数

距离相关系数是为了克服Pearson相关系数的弱点而生的。在 x 和 x^2 这个例子中，即便Pearson相关系数是 0 ，我们也不能断定这两个变量是独立的（有可能是非线性相关）；但如果距离相关系数是 0 ，那么我们就可以说这两个变量是独立的。
python实现
尽管有MIC和距离相关系数在了，但当变量之间的关系接近线性相关的时候，Pearson相关系数仍然是不可替代的。有以下两点原因：

Pearson相关系数计算速度快，这在处理大规模数据的时候很重要。
Pearson相关系数的取值区间是[-1，1]，而MIC和距离相关系数都是[0，1]。这个特点使得Pearson相关系数能够表征更丰富的关系，符号表示关系的正负，绝对值能够表示强度。当然，Pearson相关性有效的前提是两个变量的变化关系是单调的。

2.1.5 方差选择法

过滤特征选择法还有一种方法不需要度量特征 x_i 和类别标签 y 的信息量。这种方法先要计算各个特征的方差，然后根据阈值，选择方差大于阈值的特征。VarianceThreshold是特征选择的简单基线方法。它删除方差不符合某个阈值的所有特征。默认情况下，它会删除所有零差异特征，即所有样本中具有相同值的特征。

from sklearn.feature_selection import VarianceThreshold
X = [[0, 0, 1], [0, 1, 0], [1, 0, 0], [0, 1, 1], [0, 1, 0], [0, 1, 1]]
# 方差选择法，返回值为特征选择后的数据
# 参数threshold为方差的阈值
sel = VarianceThreshold(threshold=(.8 * (1 - .8)))
print(sel.fit_transform(X))

array([[0, 1],  [1, 0],  [0, 0],  [1, 1],  [1, 0],  [1, 1]])

方差选择的逻辑并不是很合理，这个是基于各特征分布较为接近的时候，才能以方差的逻辑来衡量信息量。但是如果是离散的或是仅集中在几个数值上，如果分布过于集中，其信息量则较小。而对于连续变量，由于阈值可以连续变化，所以信息量不随方差而变。实际使用时，可以结合cross-validate进行检验。

2.2 Wrapper(包裹式)

包裹式基本思想：基于hold-out方法，对于每一个待选的特征子集，都在训练集上训练一遍模型，然后在测试集上根据误差大小选择出特征子集。西瓜书上说包装法应该欲训练什么算法，就选择该算法进行评估；随着学习器（评估器）的改变，最佳特征组合可能会改变。

2.2.1 向前逐步选择

每增加一个变量考虑了局部最优。
(i) 记不含任何特征的模型为 $M_0$ ，计算这个 $M_0$ 的测试误差。
(ii) 在 $M_0$ 基础上增加一个变量，计算p个模型的RSS，选择RSS最小的模型记作 $M_1$ ，并计算该模型 $M_1$ 的测试误差。
(iii) 在最小的RSS模型下继续增加一个变量，选择RSS最小的模型记作 $M_2$ ，并计算该模型 $M_2$ 的测试误差。
(iv) 以此类推，重复以上过程知道拟合的模型有p个特征为止，并选择p+1个模型 ${M_0,M_1,...,M_p \}$ 中测试误差最小的模型作为最优模型。

#!usr/bin/env python
# -*- coding:utf-8 -*-
"""
@author: admin
@file: 向前逐步选择.py
@time: 2021/03/15
@desc:
"""
import numpy as np
import pandas as pd
import statsmodels.api as sm
from sklearn.linear_model import Lasso
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score


def froward_select(train_data, test_data, target):
    """
    向前逐步回归
    :param data: 数据
    :param target:目标值
    :return:
    """
    variate = set(train_data.columns)
    variate.remove(target)
    # 参数
    selected = []  # 储存挑选的变量
    # 初始化
    # 初始化决定系数R^2,越近于1越好
    cur_score, best_score = 0.0, 0.0
    # 循环删选变量,直至对所有变量进行了选择
    while variate:
        variate_r2 = []
        # 找到局部最优
        for var in variate:
            selected.append(var)
            if len(selected) == 1:
                model = Lasso().fit(train_data[selected[0]].values.reshape(-1, 1), train_data[target])
                y_pred = model.predict(test_data[selected[0]].values.reshape(-1, 1))
                # R2 = r2(test_data[target], y_pred)
                R2 = r2_score(test_data[target], y_pred)
                variate_r2.append((R2, var))
                selected.remove(var)
            else:
                model = Lasso().fit(train_data[selected], train_data[target])
                y_pred = model.predict(test_data[selected])
                # R2 = r2(test_data[target], y_pred)
                R2 = r2_score(test_data[target], y_pred)
                variate_r2.append((R2, var))
                selected.remove(var)
        variate_r2.sort(reverse=False)  # 默认升序
        best_score, best_var = variate_r2.pop()  # pop用于移除列表中的一个元素（默认最后一个元素），并且返回该元素的值
        if cur_score < best_score:  # 说明了加了该变量更好了
            variate.remove(best_var)  # 判断过了，不管是好是坏，就删了
            selected.append(best_var)
            cur_score = best_score
            print("R2={},continue!".format(cur_score))
        else:
            print('for selection over!')
            break
    selected_features = '+'.join([str(i) for i in selected])
    print(selected_features)


def main():
    boston = load_boston()
    X = boston.data
    y = boston.target
    features = boston.feature_names
    x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.4)
    boston_train_data = pd.DataFrame(x_train, columns=features)
    boston_train_data["Price"] = y_train
    boston_test_data = pd.DataFrame(x_test, columns=features)
    boston_test_data["Price"] = y_test
    froward_select(boston_train_data, boston_test_data, 'Price')


if __name__ == '__main__':
    main()

R2=0.61744910032392,continue!
R2=0.6908671406351847,continue!
R2=0.7317782212152852,continue!
R2=0.7395157511526225,continue!
R2=0.7433588119420051,continue!
R2=0.7454229322919887,continue!
R2=0.7462568212024802,continue!
R2=0.7462857832907019,continue!
for selection over!
LSTAT+PTRATIO+RM+DIS+B+CRIM+INDUS+TAX

2.2.2 向后逐步选择

向后逐步选择简述如下：

初始化时将所有特征放入模型中
每次剔除最差变量，该变量的剔除使得模型效果不明显，评估模型性能的改善
重复直到没有变量可剔除后

#!usr/bin/env python
# -*- coding:utf-8 -*-
"""
@author: admin
@file: 向后逐步挑选.py
@time: 2021/03/16
@desc:
"""
import numpy as np
import pandas as pd
import statsmodels.api as sm
from sklearn.linear_model import Lasso
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score


def froward_select(train_data, test_data, target):
    """
    向前逐步回归
    :param data: 数据
    :param target:目标值
    :return:
    """
    variate = list(set(train_data.columns))
    variate.remove(target)
    # 参数
    selected = []  # 储存挑选的变量
    # 初始化
    # 初始化决定系数R^2,越近于1越好
    cur_score, best_score = 0.0, 0.0
    # 循环删选变量,直至对所有变量进行了选择
    while variate:
        variate_r2 = []
        # 找到局部最优
        for var in variate:
            variate.remove(var)
            if len(variate) == 1:
                model = Lasso().fit(train_data[variate[0]].values.reshape(-1, 1), train_data[target])
                y_pred = model.predict(test_data[variate[0]].values.reshape(-1, 1))
                R2 = r2_score(test_data[target], y_pred)
                variate_r2.append((R2, var))
                variate.append(var)
            else:
                model = Lasso().fit(train_data[variate], train_data[target])
                y_pred = model.predict(test_data[variate])
                R2 = r2_score(test_data[target], y_pred)
                variate_r2.append((R2, var))
                variate.append(var)
        variate_r2.sort(reverse=False)  # 升序排序r2，默认升序
        best_score, best_var = variate_r2.pop()  # pop用于移除列表中的一个元素（默认最后一个元素），并且返回该元素的值
        if cur_score < best_score:  # 说明了移除了该变量更好了
            variate.remove(best_var)  # 判断过了，不管是好是坏，就删了
            selected.append(best_var)
            cur_score = best_score
            print("R2={},continue!".format(cur_score))
        else:
            print('for selection over!')
            break
    print(selected)
    selected = [var for var in set(train_data.columns) if var not in selected]
    selected_features = '+'.join([str(i) for i in selected])

    print(selected_features)


def main():
    boston = load_boston()
    X = boston.data
    y = boston.target
    features = boston.feature_names
    x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.4)
    boston_train_data = pd.DataFrame(x_train, columns=features)
    boston_train_data["Price"] = y_train
    boston_test_data = pd.DataFrame(x_test, columns=features)
    boston_test_data["Price"] = y_test
    froward_select(boston_train_data, boston_test_data, 'Price')


if __name__ == '__main__':
    main()

R2=0.6130365918500247,continue!
R2=0.6206140392385366,continue!
R2=0.6206319773780711,continue!
R2=0.6216812478858313,continue!
R2=0.6217076288117218,continue!
for selection over!
['CHAS', 'AGE', 'INDUS', 'ZN', 'NOX']
TAX+Price+RAD+DIS+PTRATIO+RM+LSTAT+CRIM+B

2.2.3 双向挑选

双向挑选简述如下：
向前向后挑选的结合
双向挑选用的较多，能够兼顾模型复杂度与模型精度的要求。
描述为：先两步向前挑选，再向后挑选，再反复向前向后

#!usr/bin/env python
# -*- coding:utf-8 -*-
"""
@author: admin
@file: 双向挑选.py
@time: 2021/03/16
@desc:
"""
import numpy as np
import pandas as pd
import statsmodels.api as sm
from sklearn.linear_model import Lasso
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score

def froward_select(train_data, test_data, target):
    """
    向前逐步回归
    :param data: 数据
    :param target:目标值
    :return:
    """
    variate = list(set(train_data.columns))
    variate.remove(target)
    selected = []  # 储存挑选的变量
    selected_h = []  # 存储删除的变量
    # 初始化
    # 初始化决定系数R^2,越近于1越好
    cur_score_f, best_score_f = 0.0, 0.0
    cur_score_h, best_score_h = 0.0, 0.0
    # 循环删选变量,直至对所有变量进行了选择
    # 双向挑选—先两步前向再一步后向
    while variate:
        variate_r2_f = []
        variate_r2_h = []
        # 找到局部最优
        # 先两步前向
        for i in range(2):
            for var in variate:
                selected.append(var)
                if len(selected) == 1:
                    model = Lasso().fit(train_data[selected[0]].values.reshape(-1, 1), train_data[target])
                    y_pred = model.predict(test_data[selected[0]].values.reshape(-1, 1))
                    R2 = r2_score(test_data[target], y_pred)
                    variate_r2_f.append((R2, var))
                    selected.remove(var)
                else:
                    model = Lasso().fit(train_data[selected], train_data[target])
                    y_pred = model.predict(test_data[selected])
                    R2 = r2_score(test_data[target], y_pred)
                    variate_r2_f.append((R2, var))
                    selected.remove(var)
            variate_r2_f.sort(reverse=False)  # 降序排序r2，默认升序
            best_score_f, best_var_f = variate_r2_f.pop()  # pop用于移除列表中的一个元素（默认最后一个元素），并且返回该元素的值
            if cur_score_f < best_score_f:  # 说明了加了该变量更好了就不移除了,否则就移除
                selected.append(best_var_f)
                cur_score_f = best_score_f
                print("R2_f={},continue!".format(cur_score_f))
            else:
                variate.remove(best_var_f)
                break
        # 再一步后向
        for var in variate:
            variate.remove(var)
            if len(variate) == 1:
                model = Lasso().fit(train_data[variate[0]].values.reshape(-1, 1), train_data[target])
                y_pred = model.predict(test_data[variate[0]].values.reshape(-1, 1))
                R2 = r2_score(test_data[target], y_pred)
                variate_r2_h.append((R2, var))
                variate.append(var)
            else:
                model = Lasso().fit(train_data[variate], train_data[target])
                y_pred = model.predict(test_data[variate])
                R2 = r2_score(test_data[target], y_pred)
                variate_r2_h.append((R2, var))
                variate.append(var)
        variate_r2_h.sort(reverse=False)  # 升序排序r2，默认升序
        best_score_h, best_var_h = variate_r2_h.pop()  # pop用于移除列表中的一个元素（默认最后一个元素），并且返回该元素的值
        if cur_score_h < best_score_h:  # 说明了移除了该变量更好了
            variate.remove(best_var_h)
            selected_h.append(best_var_h)
            cur_score_h = best_score_h
            print("R2_h={},continue!".format(cur_score_h))
        else:
            print('for selection over!')
            selected = [var for var in set(train_data.columns) if var not in selected_h]
            selected_features = '+'.join([str(i) for i in selected])
            print(selected_features)
            break



def main():
    boston = load_boston()
    X = boston.data
    y = boston.target
    features = boston.feature_names
    x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.4)
    boston_train_data = pd.DataFrame(x_train, columns=features)
    boston_train_data["Price"] = y_train
    boston_test_data = pd.DataFrame(x_test, columns=features)
    boston_test_data["Price"] = y_test
    froward_select(boston_train_data, boston_test_data, 'Price')


if __name__ == '__main__':
    main()

R2_f=0.5290772958895777,continue!
R2_f=0.5992603091580796,continue!
R2_h=0.6392096900660633,continue!
R2_f=0.6328497309792275,continue!
R2_f=0.6424099014083555,continue!
R2_h=0.6446960403771425,continue!
R2_f=0.6529845736263218,continue!
R2_f=0.6555371387702666,continue!
R2_h=0.6524813775669193,continue!
R2_f=0.6577033230821112,continue!
R2_f=0.6577063213485781,continue!
R2_h=0.6525859983540159,continue!
R2_f=0.6577196381996436,continue!
for selection over!
Price+RM+CHAS+AGE+PTRATIO+TAX+NOX+CRIM+B+DIS

2.2.4 递归特征消除法

递归消除特征法使用一个基模型来进行多轮训练，每轮训练后通过学习器返回的 coef_ 或者feature_importances_ 消除若干权重较低的特征，再基于新的特征集进行下一轮训练。

from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression

#递归特征消除法，返回特征选择后的数据
#参数estimator为基模型
#参数n_features_to_select为选择的特征个数
RFE(estimator=LogisticRegression(), n_features_to_select=2).fit_transform(iris.data, iris.target)

2.3 嵌入法

基于惩罚项的特征选择法通过L1正则项来选择特征：L1正则方法具有稀疏解的特性，因此天然具备特征选择的特性。先使用某些机器学习的模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征，L1正则化可以使得特征的权值系数为0。

from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression

#带L1惩罚项的逻辑回归作为基模型的特征选择   
SelectFromModel(LogisticRegression(penalty="l1", C=0.1)).fit_transform(iris.data, iris.target)

要注意，L1没有选到的特征不代表不重要，原因是两个具有高相关性的特征可能只保留了一个，如果要确定哪个特征重要应再通过L2正则方法交叉检验。
数据预处理与特征工程—9.Lasso算法实现特征选择

3.特征提取

特征提取与特征选择的区别是：特征提取后的新特征是原来特征的一个映射。特征选择后的特征是原来特征的一个子集。主成分分析(Principle Components Analysis ,PCA)和线性判别分析（Linear Discriminant Analysis,LDA）是特征提取的两种主要经典方法。

3.1 主成分分析PCA

PCA得到的投影空间是协方差矩阵的特征向量,特征抽取后的特征要能够精确地表示样本信息，使得信息丢失很小。
具体可参考这篇博客数据预处理—8.属性归约之主成分分析(理论及python实现)

3.2 线性判别分析LDA

线性判别分析LDA则是通过求得一个变换W,使得变换之后的新均值之差最大、方差最大（也就是最大化类间距离和最小化类内距离），变换W就是特征的投影方向。特征抽取后的特征，要使得分类后的准确率很高，不能比原来特征进行分类的准确率低。
具体使用可以参考这篇博客用scikit-learn进行LDA降维
一般来说，如果我们的数据是有类别标签的，那么优先选择LDA去尝试降维；当然也可以使用PCA做很小幅度的降维去消去噪声，然后再使用LDA降维。如果没有类别标签，那么肯定PCA是最先考虑的一个选择了。

4.特征构造—创造新特征

4.1. 数值特征的简单变换

单独特征列乘以一个常数（constant multiplication）或者加减一个常数：对于创造新的有用特征毫无用处；只能作为对已有特征的处理。

df['Feature'] = df['Feature'] + n
df['Feature'] = df['Feature'] - n
df['Feature'] = df['Feature'] * n
df['Feature'] = df['Feature'] / n

任何针对单独特征列的单调变换（如对数）：不适用于决策树类算法。对于决策树而言， $X$ 、 $X^3$ 、 $X^5$ 之间没有差异， $X^2$ 、 $X^4$ 、 $X^6$ 之间没有差异，除非发生了舍入误差。
如果 $u (x 1, y 1) > u (x 2, y 2)$ ，则 $v (x 1, y 1) ＝ f (u (x 1, y 1)) > v (x 2, y 2) ＝ f (u (x 2, y 2))$ ,那么 $f ()$ 就是其单调变换。

import numpy as np
# 计算n次方
df['Feature'] = df['Feature']**2
# 计算log变换
df['Feature'] = np.log(df['Feature'])

线性组合（linear combination）：借助线性组合，线性学习器可以很好扩展到大量数据，并有助于构建复杂模型解决非线性问题。仅适用于决策树以及基于决策树的ensemble（如gradient boosting,random forest），因为常见的axis-aligned split function不擅长捕获不同特征之间的相关性；不适用于SVM、线性回归、神经网络等。如：
将两个特征的值相乘形成的特征组合；
```
df['Feature'] = df['A'] * df['B']
```
将五个特征的值相乘形成的特征组合；
```
df['Feature'] = df['A'] * df['B'] * df['C'] * df['D'] * df['E']
```

多项式特征（polynomial feature）:1.3 sklearn中的preprocessing.PolynomialFeatures——多项式回归
当两个变量各自与 y 的关系并不强时候，把它们结合成为一个新的变量可能更会容易体现出它们与 y 的关系。特征a和特征b的多项式输出是： $1, a, b, a^2, ab, b^2]$ 或者 $[1, a, b, a b]$ 。

import numpy as np
from sklearn.preprocessing import PolynomialFeatures
X = np.arange(6).reshape(3, 2)
print(X)
# 输出：array([[0, 1],
              [2, 3],
              [4, 5]])
# 设置多项式阶数为２
poly = PolynomialFeatures(2)
print(poly.fit_transform(X))
# 输出：array([[ 1.,  0.,  1.,  0.,  0.,  1.],
              [ 1.,  2.,  3.,  4.,  6.,  9.],
              [ 1.,  4.,  5., 16., 20., 25.]])
＃默认的阶数是２，同时设置交互关系为true
poly = PolynomialFeatures(interaction_only=True)
print(poly.fit_transform(X))
# 输出：array([[ 1.,  0.,  1.,  0.],
              [ 1.,  2.,  3.,  6.],
              [ 1.,  4.,  5., 20.]])

比例特征（ratio feature）: $\frac{X1}{X2}$
计算两个特征的数值比例： $\frac{X1}{X2}$ 。
```
df['Feature'] = df['X1']/df['X2']
```
绝对值（absolute value）
计算特征值的绝对值： $∣ X ∣$ 。
例子：某数据的相关系数特征。
```
import numpy as np
df['Feature'] = np.abs(df['Feature'])
```

$max(X_1,X_2)，min(X_1,X_2)，X_1 xor X_2$

# 最大值特征
df['Feature'] = df.apply(lambda x: max(x['X1'], x['X2']), axis=1)
# 最小值特征
df['Feature'] = df.apply(lambda x: min(x['X1'], x['X2']), axis=1)
# 异或特征—计算两特征的异或值：X1 xor X2。
df['Feature'] = df.apply(lambda x: x['X1'] ^ x['X2'], axis=1)

排名编码特征
按特征值对全体样本进行排序，以排序序号作为特征。这种特征对异常点不敏感，不会导致特征值冲突。例子：广告历史曝光量排名。

X = [10, 9, 9, 8, 7]
df = pd.DataFrame({'X': X,})
df['num'] = df['X'].rank(ascending=0, method='dense')

    X    num
0    10    1.0
1    9    2.0
2    9    2.0
3    8    3.0
4    7    4.0

4.2 类别特征与数值特征的组合

用N1和N2表示数值特征，用C1和C2表示类别特征，利用pandas的groupby操作，可以创造出以下几种有意义的新特征：（其中，C2还可以是离散化了的N1）

分组统计中位数

df.groupby(['C1']).agg({'N1': 'median'})

分组统计平均数

df.groupby(['C1']).agg({'N1': 'mean'})

分组统计众数

from scipy import stats
df.groupby(['C1'])['N1'].agg(lambda x: stats.mode(x)[0][0]))})

分组统计最小值

df.groupby(['C1']).agg({'N1': 'min'})

分组统计最大值

df.groupby(['C1']).agg({'N1': 'max'})

分组统计标准差

df.groupby(['C1']).agg({'N1': 'std'})

分组统计方差

df.groupby(['C1']).agg({'N1': 'var'})

分组统计频数

df.groupby(['C1']).agg({'N1': 'count'})

仅仅将已有的类别和数值特征进行以上的有效组合，就能够大量增加优秀的可用特征。

统计频数
直接统计类别特征的频数，这个不需要 groupby 也有意义。

df.groupby(['C1']).agg({'C1': 'count'})

4.3 分组统计和基础特征工程方法结合

将分组统计和线性组合等基础特征工程方法结合（仅用于决策树），可以得到更多有意义的特征。

中位数分组与线性组合结合

df = pd.merge(df, df.groupby(['C1'])['N1'].median().reset_index().rename(columns={'N1': 'N1_Median'}),
              on='C1', how='left')
df['N1+Median(C1)'] = df['N1'] + df['N1_Median']
df['N1-Median(C1)'] = df['N1'] - df['N1_Median']
df['N1*Median(C1)'] = df['N1'] * df['N1_Median']
df['N1/Median(C1)'] = df['N1'] / df['N1_Median']

    C1    C2    N1    N2  N1_Median N1+Median(C1) N1-Median(C1) N1*Median(C1) N1/Median(C1)
0    A    a    1    1.1  1.0      2.0           0.0           1.0           1.00
1    A    a    1    2.2  1.0      2.0           0.0           1.0           1.00
2    A    a    2    3.3  1.0      3.0           1.0           2.0           2.00
3    B    a    2    4.4  2.5      4.5           -0.5          5.0           0.80
4    B    a    3    5.5  2.5      5.5           0.5           7.5           1.20
5    C    b    3    6.6  4.0      7.0           -1.0          12.0          0.75
6    C    b    4    7.7  4.0      8.0           0.0           16.0          1.00
7    C    b    4    8.8  4.0      8.0           0.0           16.0          1.00
8    D    b    5    9.9  5.0      10.0           0.0          25.0          1.00
9    D    b    5    10.0 5.0      10.0           0.0          25.0          1.00

平均数分组与线性组合结合

df = pd.merge(df, df.groupby(['C1'])['N1'].mean().reset_index().rename(columns={'N1': 'N1_Mean'}),
              on='C1', how='left')
df['N1+Mean(C1)'] = df['N1'] + df['N1_Mean']
df['N1-Mean(C1)'] = df['N1'] - df['N1_Mean']
df['N1*Mean(C1)'] = df['N1'] * df['N1_Mean']
df['N1/Mean(C1)'] = df['N1'] / df['N1_Mean']

    C1    C2    N1    N2   N1_Mean  N1+Mean(C1) N1-Mean(C1) N1*Mean(C1) N1/Mean(C1)
0    A    a    1    1.1  1.333333 2.333333    -0.333333   1.333333    0.750000
1    A    a    1    2.2  1.333333 2.333333    -0.333333   1.333333    0.750000
2    A    a    2    3.3  1.333333 3.333333    0.666667    2.666667    1.500000
3    B    a    2    4.4  2.500000 4.500000    -0.500000   5.000000    0.800000
4    B    a    3    5.5  2.500000 5.500000    0.500000    7.500000    1.200000
5    C    b    3    6.6  3.666667 6.666667    -0.666667   11.000000   0.818182
6    C    b    4    7.7  3.666667 7.666667    0.333333    14.666667   1.090909
7    C    b    4    8.8  3.666667 7.666667    0.333333    14.666667   1.090909
8    D    b    5    9.9  5.000000 10.000000   0.000000    25.000000   1.000000
9    D    b    5    10.0 5.000000 10.000000   0.000000    25.000000   1.000000

4.3 笛卡尔乘积创造新特征

通过将单独的特征求笛卡尔乘积的方式来组合2个或更多个特征，从而构造出组合特征。最终获得的预测能力将远远超过任一特征单独的预测能力。

4.3.1 类别特征进行笛卡尔乘积特征组合

例如：类别特征color和类别特征light进行笛卡尔乘积特征组合
特征 color 取值：red, green, blue
特征 light 取值：on, off
这两个特征各自可以离散化为3维和2维的向量，对它们做笛卡尔乘积转化，就可以组合出长度为6的特征，它们分别对应着原始值对 (red, on)，(red, off)，(green, on)，(green, off)，(blue, on)，(blue, off)。

import pandas as pd

color = ['on', 'on', 'off', 'off', 'off', ]
light = ['red', 'green', 'blue', 'red', 'green', ]
df = pd.DataFrame({'color': color, 'light': light})
print(df)


def cartesian_product_feature_crosses(df, feature1_name, feature2_name):
    feature1_df = pd.get_dummies(df[feature1_name], prefix=feature1_name)
    feature1_columns = feature1_df.columns
    feature2_df = pd.get_dummies(df[feature2_name], prefix=feature2_name)
    feature2_columns = feature2_df.columns
    # 对两个onehot编码得到的dataframe进行拼接
    combine_df = pd.concat([feature1_df, feature2_df], axis=1)
    crosses_feature_columns = []
    for feature1 in feature1_columns:
        for feature2 in feature2_columns:
            # 构造新的列名
            crosses_feature = '{}&{}'.format(feature1, feature2)
            crosses_feature_columns.append(crosses_feature)
            # 笛卡尔乘积
            combine_df[crosses_feature] = combine_df[feature1] * combine_df[feature2]
    combine_df = combine_df.loc[:, crosses_feature_columns]
    return combine_df
combine_df = cartesian_product_feature_crosses(df, 'color', 'light')
print(combine_df)

  color  light
0    on    red
1    on  green
2   off   blue
3   off    red
4   off  green
   color_off&light_blue  ...  color_on&light_red
0                     0  ...                   1
1                     0  ...                   0
2                     1  ...                   0
3                     0  ...                   0
4                     0  ...                   0

4.3.2 连续特征与类别特征之间的笛卡尔乘积特征组合

只要把连续特征看成是一维的类别特征就好了，这时候组合后特征对应的值就不是 0/1 了，而是连续特征的取值。

4.3.3 连续特征之间的笛卡尔乘积特征组合

笛卡尔乘积组合特征方法一般应用于类别特征之间，连续值特征使用笛卡尔乘积组合特征时一般需要先进行离散化,然后再进行特征组合。例如：经度和纬度特征进行笛卡尔乘积特征组合

import pandas as pd
import numpy as np
lat = [
  '0  < lat <= 10',
  '10 < lat <= 20',
  '20 < lat <= 30'
]
lon = [
  '0  < lon <= 15',
  '15 < lon <= 30',
    np.nan
]
df = pd.DataFrame({'lat': lat, 'lon': lon})
print(df)

def cartesian_product_feature_crosses(df, feature1_name, feature2_name):
    feature1_df = pd.get_dummies(df[feature1_name], prefix=feature1_name)
    feature1_columns = feature1_df.columns
    feature2_df = pd.get_dummies(df[feature2_name], prefix=feature2_name)
    feature2_columns = feature2_df.columns
    # 对两个onehot编码得到的dataframe进行拼接
    combine_df = pd.concat([feature1_df, feature2_df], axis=1)
    crosses_feature_columns = []
    for feature1 in feature1_columns:
        for feature2 in feature2_columns:
            # 构造新的列名
            crosses_feature = '{}&{}'.format(feature1, feature2)
            crosses_feature_columns.append(crosses_feature)
            # 笛卡尔乘积
            combine_df[crosses_feature] = combine_df[feature1] * combine_df[feature2]
    combine_df = combine_df.loc[:, crosses_feature_columns]
    return combine_df
combine_df = cartesian_product_feature_crosses(df, 'lat', 'lon')
print(combine_df)

              lat             lon
0  0  < lat <= 10  0  < lon <= 15
1  10 < lat <= 20  15 < lon <= 30
2  20 < lat <= 30             NaN
   lat_0  < lat <= 10&lon_0  < lon <= 15  ...  lat_20 < lat <= 30&lon_15 < lon <= 30
0                                      1  ...                                      0
1                                      0  ...                                      0
2                                      0  ...                                      0

[3 rows x 6 columns]

4.4 用基因编程创造新特征

遗传编程创造新特征是基于 genetic programming 的 symbolic regression（符号回归）。symbolic regression的具体实现方式是遗传算法（genetic algorithm）。一开始，一群天真而未经历选择的公式会被随机生成。此后的每一代中，最「合适」的公式们将被选中。随着迭代次数的增长，它们不断繁殖、变异、进化，从而不断逼近数据分布的真相。
目前，python环境下最好用的基因编程库为gplearn。gplearn 这个库提供了解决思路：随机化生成大量特征组合方式，解决了没有先验知识，手工生成特征费时费力的问题。

通过遗传算法进行特征组合的迭代，而且这种迭代是有监督的迭代，存留的特征和label相关性是也来越高的，大量低相关特征组合会在迭代中被淘汰掉，用决策树算法做个类比的话，我们自己组合特征然后筛选，好比是后剪枝过程，遗传算法进行的则是预剪枝的方式。

基因编程的两大用法：

转换（SymbolicTransformer）：把已有的特征进行组合转换，组合的方式（一元、二元、多元算子）可以由用户自行定义，也可以使用库中自带的函数（如加减乘除、min、max、三角函数、指数、对数）。组合的目的，是创造出和目标y值最“相关”的新特征。这种相关程度可以用spearman或者pearson的相关系数进行测量。spearman多用于决策树（免疫单特征单调变换），pearson多用于线性回归等其他算法。它并不直接预测目标变量，而是转化原有的特征、输出新的特征，这在特征工程的阶段尤为有效。
回归（Symbolic Regressor）：它利用遗传算法得到的公式，直接预测目标变量的值。

# 数据集：波士顿数据集
# 训练Ridge模型
est = Ridge()
est.fit(boston.data[:300, :], boston.target[:300])
print(est.score(boston.data[300:, :], boston.target[300:]))
# 输出：0.759145222183
# 使用超过20代的2000人。选择最好的100个hall_of_fame，然后使用最不相关的10作为我们的新功能。因为我们使用线性模型作为估算器，所以这里使用默认值metric='pearson'。
function_set = ['add', 'sub', 'mul', 'div',
                'sqrt', 'log', 'abs', 'neg', 'inv',
                'max', 'min']
gp = SymbolicTransformer(generations=20, population_size=2000,
                         hall_of_fame=100, n_components=10,
                         function_set=function_set,
                         parsimony_coefficient=0.0005,
                         max_samples=0.9, verbose=1,
                         random_state=0, n_jobs=3)
gp.fit(boston.data[:300, :], boston.target[:300])
# 将新构造的特征拼接到原始数据上
gp_features = gp.transform(boston.data)
new_boston = np.hstack((boston.data, gp_features))
# 使用新的特征重新训练Ridge模型
est = Ridge()
est.fit(new_boston[:300, :], boston.target[:300])
print(est.score(new_boston[300:, :], boston.target[300:]))
# 输出：0.841750404385

使用新构造的特征训练模型效果很显著。

4.5 GBDT特征构造

GBDT 是一种常用的非线性模型，基于集成学习中 boosting 的思想，由于GBDT本身可以发现多种有区分性的特征以及特征组合，决策树的路径可以直接作为 LR 输入特征使用，省去了人工寻找特征、特征组合的步骤。所以可以将 GBDT 的叶子结点输出，作为LR的输入。选用GBDT有如下两个关键点：

采用ensemble决策树而非单颗树
一棵树的表达能力很弱，不足以表达多个有区分性的特征组合，多棵树的表达能力更强一些。GBDT 每棵树都在学习前面棵树尚存的不足，迭代多少次就会生成多少颗树。多棵树正好满足 LR 每条训练样本可以通过 GBDT 映射成多个特征的需求。

采用 GBDT 而非 RF
RF 也是多棵树，但从效果上有实践证明不如 GBDT。且 GBDT 前面的树，特征分裂主要体现对多数样本有区分度的特征；后面的树，主要体现的是经过前 N 颗树，残差仍然较大的少数样本。优先选用在整体上有区分度的特征，再选用针对少数样本有区分度的特征，思路更加合理，这应该也是用 GBDT 的原因。

import numpy as np
import random
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.preprocessing import OneHotEncoder
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_curve, roc_auc_score

# 生成随机数据
np.random.seed(10)
X, Y = make_classification(n_samples=1000, n_features=30)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=233, test_size=0.4)
# LR模型
LR = LogisticRegression()
LR.fit(X_train, Y_train)
y_pred = LR.predict_proba(X_test)[:, 1]
fpr, tpr, _ = roc_curve(Y_test, y_pred)
auc = roc_auc_score(Y_test, y_pred)
print('LogisticRegression: ', auc)

# 训练GBDT模型
gbdt = GradientBoostingClassifier(n_estimators=10)
gbdt.fit(X_train, Y_train)
# 将训练好的树应用到X_train，返回叶索引,shape大小为(600,10,1)
print(gbdt.apply(X_train)[:, :, 0])
# 对GBDT预测结果进行onehot编码
onehot = OneHotEncoder()
onehot.fit(gbdt.apply(X_train)[:, :, 0])
print(onehot.transform(gbdt.apply(X_train)[:, :, 0]))
# 训练LR模型
lr = LogisticRegression()
lr.fit(onehot.transform(gbdt.apply(X_train)[:, :, 0]), Y_train)
# 测试集预测
Y_pred = lr.predict_proba(onehot.transform(gbdt.apply(X_test)[:, :, 0]))[:, 1]
fpr, tpr, _ = roc_curve(Y_test, Y_pred)
auc = roc_auc_score(Y_test, Y_pred)
print('GradientBoosting + LogisticRegression: ', auc)

LogisticRegression:  0.9349156965074267
GradientBoosting + LogisticRegression:  0.9412133681252508

GBDT 算法的特点可以用来发掘有区分度的特征、特征组合，减少特征工程中人力成本，且业界现在已有实践，GBDT+LR、GBDT+FM 等都是值得尝试的思路。不同场景，GBDT 融合 LR/FM 的思路可能会略有不同，可以多种角度尝试。

4.6 聚类特征构造

聚类算法有：

聚类特征构造步骤为：

从预处理后的特征集中选择一个或多个特征；当只选择一个数值型特征时，聚类算法构造特征相当于使用聚类算法进行特征分箱
选择适合聚类算法对已选择的特征进行聚类，并输出聚类类标结果；
对聚类类标结果进行编码；一般聚类类标结果为一个数值，但实际上这个数值并没有大小之分，所以一般需要进行特征编码

下面以使用 k-mean 算法对用户兴趣爱好进行聚类为例：

import pandas as pd
import jieba
import numpy as np
from mitie import total_word_feature_extractor
from sklearn.cluster import KMeans
from sklearn.preprocessing import OneHotEncoder
# 构造特征集
hobby = [
    '健身', '电影', '音乐', '读书', '历史',
    '篮球', '羽毛球', '足球',
]
df = pd.DataFrame({'兴趣': hobby})
display(df.head(20))
# 输出：
    兴趣
0	健身
1	电影
2	音乐
3	读书
4	历史
5	篮球
6	羽毛球
7	足球
# 加载Embedding模型
mitie_model_filename = 'total_word_feature_extractor_zh.dat'
twfe = total_word_feature_extractor(mitie_model_filename)
# 把词语转换成embedding向量
embeding_array = np.array(list(df['兴趣'].apply(
    lambda w: twfe.get_feature_vector(w))))
# k-mean距离
kmeans = KMeans(n_clusters=2, random_state=0).fit(embeding_array)
kmean_label = kmeans.labels_
print('kmeans.labels_:{}'.format(kmean_label))
# 输出：kmeans.labels_:[1 1 1 1 1 0 0 0]
kmean_label = kmean_label.reshape(-1, 1)
print('kmean_label shape={}'.format(kmean_label.shape))
# 输出：kmean_label shape=(8, 1)
# 特征编码
enc = OneHotEncoder()
onehot_code = enc.fit_transform(kmean_label)
print(onehot_code.toarray())
# 输出：
[[0. 1.]
 [0. 1.]
 [0. 1.]
 [0. 1.]
 [0. 1.]
 [1. 0.]
 [1. 0.]
 [1. 0.]]

聚类算法在特征构造中的应用：

利用聚类算法对文本聚类，使用聚类类标结果作为输入特征；
利用聚类算法对单个数值特征进行聚类，相当于使用聚类算法进行特征分箱；
利用聚类算法对R、F、M数据进行聚类，类似RFM模型，然后再使用代表衡量客户价值的聚类类标结果作为输入特征；

4.7 日期/时间变量处理

对日期/时间型变量，可以通过如下处理将时间变量变成离散型。
时间是否为一个节日，是否在一个时间段（类别型）；或者计算距离某个日子变成间隔型；或者某个时间段内发生了多少次变成组合型等等；这个需要结合具体应用场景。使其变成离散型。

可以基于某个基准日期,转化为天数
以观察点为基准,将所有开户日期转为距离观察点的天数(month-on-book)

【持续更新】机器学习特征工程实用技巧大全
【机器学习】特征选择(Feature Selection)方法汇总
Datawhale 零基础入门数据挖掘-Task3 特征工程
基于sklearn决策树的最优分箱与IV值计算-Python实现
平均数编码：针对高基数定性特征（类别特征）的数据预处理/特征工程
机器学习之数据预处理
【有监督分箱】方法一：卡方分箱
【有监督分箱】方法二： Best-KS分箱
特征工程系列：聚合特征构造以及转换特征构造
特征工程系列：笛卡尔乘积特征构造以及遗传编程特征构造
特征工程系列：GBDT特征构造以及聚类特征构造

如果对您有帮助，麻烦点赞关注，这真的对我很重要！！！如果需要互关，请评论或者私信！

你可能感兴趣的:(#,数据预处理与特征工程,数据预处理,特征工程,特征选择,特征抽取,特征构造)

斤斤计较的婚姻到底有多难？白心之岂必有为
很多人私聊我会问到在哪个人群当中斤斤计较的人最多？我都会回答他，一般婚姻出现问题的斤斤计较的人士会非常多，以我多年经验，在婚姻落的一塌糊涂的人当中，斤斤计较的人数占比在20～30%以上，也就是说10个婚姻出现问题的斤斤计较的人有2-3个有多不减。在婚姻出问题当中，有大量的心理不平衡的、尖酸刻薄的怨妇。在婚姻中仅斤斤计较有两种类型：第一种是物质上的，另一种是精神上的。在物质与精神上抠门已经严重的影响
QQ群采集助手，精准引流必备神器 2401_87347160 其他经验分享
功能概述微信群查找与筛选工具是一款专为微信用户设计的辅助工具，它通过关键词搜索功能，帮助用户快速找到相关的微信群，并提供筛选是否需要验证的群组的功能。主要功能关键词搜索：用户可以输入关键词，工具将自动查找包含该关键词的微信群。筛选功能：工具提供筛选机制，用户可以选择是否只显示需要验证或不需要验证的群组。精准引流：通过上述功能，用户可以更精准地找到目标群组，进行有效的引流操作。3.设备需求该工具可以
机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
随笔 | 仙一般的灵气海思沧海
仙岛今天，我看了你全部，似乎已经进入你的世界我不知道，这是否是梦幻，还是你仙一般的灵气吸引了我也许每一个人都要有一份属于自己的追求，这样才能够符合人生的梦想，生活才能够充满着阳光与快乐我不知道，我为什么会这样的感叹，是在感叹自己的人生，还是感叹自己一直没有孜孜不倦的追求只感觉虚度了光阴，每天活在自己的梦中，活在一个不真实的世界是在逃避自己，还是在逃避周围的一切有时候我嘲笑自己，嘲笑自己如此的虚无，
一百九十四章. 自相矛盾巨木擎天
唉！就这么一夜，林子感觉就像过了很多天似的，先是回了阳间家里，遇到了那么多不可思议的事情儿。特别是小伙伴们，第二次与自己见面时，僵硬的表情和恐怖的气氛，让自己如坐针毡，打从心眼里难受！还有东子，他现在还好吗？有没有被人欺负？护城河里的小鱼小虾们，还都在吗？水不会真的干枯了吧？那对相亲相爱漂亮的太平鸟儿，还好吧！春天了，到了做窝、下蛋、喂养小鸟宝宝的时候了，希望它们都能够平安啊！虽然没有看见家人，也
微服务下功能权限与数据权限的设计与实现 nbsaas-boot 微服务 java 架构
在微服务架构下，系统的功能权限和数据权限控制显得尤为重要。随着系统规模的扩大和微服务数量的增加，如何保证不同用户和服务之间的访问权限准确、细粒度地控制，成为设计安全策略的关键。本文将讨论如何在微服务体系中设计和实现功能权限与数据权限控制。1.功能权限与数据权限的定义功能权限：指用户或系统角色对特定功能的访问权限。通常是某个用户角色能否执行某个操作，比如查看订单、创建订单、修改用户资料等。数据权限：
学点心理知识，呵护孩子健康静候花开_7090
昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所，超越教育与技术的思考》的讲座。今天又重新学习了一遍，收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题，她说心理健康的一些基本命题，我们与我们通常的一些教育命题是不同的，她还举了几个例子，让我们明白我们原来以为的健康并非心理学上的健康。比如如果
《投行人生》读书笔记小蘑菇的树洞
《投行人生》----作者詹姆斯-A-朗德摩根斯坦利副主席40年的职业洞见-很短小精悍的篇幅，比较适合初入职场的新人。第一部分成功的职业生涯需要规划1.情商归为适应能力分享与协作同理心适应能力，更多的是自我意识，你有能力识别自己的情并分辨这些情绪如何影响你的思想和行为。2.对于初入职场的人的建议，细节，截止日期和数据很重要截止日期，一种有效的方法是请老板为你所有的任务进行优先级排序。和老板喝咖啡的好
Long类型前后端数据不一致 igotyback 前端
响应给前端的数据浏览器控制台中response中看到的Long类型的数据是正常的到前端数据不一致前后端数据类型不匹配是一个常见问题，尤其是当后端使用Java的Long类型（64位）与前端JavaScript的Number类型（最大安全整数为2^53-1，即16位）进行数据交互时，很容易出现精度丢失的问题。这是因为JavaScript中的Number类型无法安全地表示超过16位的整数。为了解决这个问
店群合一模式下的社区团购新发展——结合链动 2+1 模式、AI 智能名片与 S2B2C 商城小程序源码说私域人工智能小程序
摘要：本文探讨了店群合一的社区团购平台在当今商业环境中的重要性和优势。通过分析店群合一模式如何将互联网社群与线下终端紧密结合，阐述了链动2+1模式、AI智能名片和S2B2C商城小程序源码在这一模式中的应用价值。这些创新元素的结合为社区团购带来了新的机遇，提升了用户信任感、拓展了营销渠道，并实现了线上线下的完美融合。一、引言随着互联网技术的不断发展，社区团购作为一种新兴的商业模式，在满足消费者日常需
2021-08-26 影幽
在生活中，女人与男人的感悟往往有所不同。人生最大的舞台就是生活，大幕随时都可能拉开，关键是你愿不愿意表演都无法躲避。在生活中，遇事不要急躁，不要急于下结论，尤其生气时不要做决断，要学会换位思考，大事化小小事化了，把复杂的事情尽量简单处理，千万不要把简单的事情复杂化。永远不要扭曲，别人善意，无药可救。昨天是张过期的支票，明天是张信用卡，只有今天才是现金，要善加利用！执着的攀登者不必去与别人比较自己的
高级编程--XML+socket练习题 masa010 java 开发语言
1.北京华北2114.8万人上海华东2,500万人广州华南1292.68万人成都华西1417万人（1）使用dom4j将信息存入xml中（2）读取信息，并打印控制台（3）添加一个city节点与子节点（4）使用socketTCP协议编写服务端与客户端，客户端输入城市ID，服务器响应相应城市信息（5）使用socketTCP协议编写服务端与客户端，客户端要求用户输入city对象，服务端接收并使用dom4j
2018-07-23-催眠日作业-#不一样的31天#-66小鹿小鹿_33
预言日：人总是在逃避命运的路上，与之不期而遇。心理学上有个著名的名词，叫做自证预言；经济学上也有一个很著名的定律叫做，墨菲定律；在灵修派上，还有一个很著名的法则，叫做吸引力法则。这3个领域的词，虽然看起来不太一样，但是他们都在告诉人们一个现象：你越担心什么，就越有可能会发生什么。同样的道理，你越想得到什么，就应该要积极地去创造什么。无论是自证预言，墨菲定律还是吸引力法则，对人都有正反2个维度的影响
【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数广龙宇一起学Rust #Rust设计模式 rust 设计模式开发语言
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言，它的所有特性，使其独一无二。因此，学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此，本系列文章的结构也与此书的结构相同（后续可能会调成结构），基本上分为三个部分
回溯 Leetcode 332 重新安排行程 mmaerd Leetcode刷题学习记录 leetcode 算法职场和发展
重新安排行程Leetcode332学习记录自代码随想录给你一份航线列表tickets，其中tickets[i]=[fromi,toi]表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从JFK（肯尼迪国际机场）出发的先生，所以该行程必须从JFK开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。例如，行程[“JFK”,“LGA”]与[“JFK”,“LGB
每日一题——第九十题互联网打工人no1 C语言程序设计每日一练 c语言
题目：判断子串是否与主串匹配#include#include#include//////判断子串是否在主串中匹配//////主串///子串///boolisSubstring(constchar*str,constchar*substr){intlenstr=strlen(str);//计算主串的长度intlenSub=strlen(substr);//计算子串的长度//遍历主字符串，对每个可能得
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
《庄子.达生9》钱江潮369
【原文】孔子观于吕梁，县水三十仞，流沫四十里，鼋鼍鱼鳖之所不能游也。见一丈夫游之，以为有苦而欲死也，使弟子并流而拯之。数百步而出，被发行歌而游于塘下。孔子从而问焉，曰：“吾以子为鬼，察子则人也。请问，‘蹈水有道乎’”曰：“亡，吾无道。吾始乎故，长乎性，成乎命。与齐俱入，与汩偕出，从水之道而不为私焉。此吾所以蹈之也。”孔子曰：“何谓始乎故，长乎性，成乎命？”曰：“吾生于陵而安于陵，故也；长于水而安于
水泥质量纠纷案代理词徐宝峰律师
贵州领航建设有限公司诉贵州纳雍隆庆乌江水泥有限公司产品质量纠纷案代理词尊敬的审判长、审判员：贵州千里律师事务所接受被告贵州纳雍隆庆乌江水泥有限公司的委托，指派我担任其诉讼代理人，参加本案的诉讼活动。下面，我结合本案事实和相关法律规定发表如下代理意见，供合议庭评议案件时参考：原告应当举证证明其遭受的损失与被告生产的水泥质量的因果关系。首先水泥是一种粉状水硬性无机胶凝材料。加水搅拌后成浆体，能在空气中
Goolge earth studio 进阶4——路径修改与平滑陟彼高冈yu Google earth studio 进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
18-115 一切思考不能有效转化为行动，都TM是扯淡！成长时间线
7月25号写了一篇关于为什么会断更如此严重的反思，然而，之后日更仅仅维持了一周，又出现了这次更严重的现象。从8月2号到昨天8月6号，5天！又是5天没有更文！虽然这次断更时间和上次一样，那为什么说这次更严重？因为上次之后就分析了问题的原因，以及应该如何解决，按理说应该会好转，然而，没过几天严重断更的现象再次出现，想想，经过反思，问题依然没有解决与改变，这让我有些担忧。到底是哪里出了问题，难道我就真的
山东大学小树林支教调研团青青仓木队——翟晓楠山东大学青青仓木队
过了半年，又一次启程，又一次回到支教的初心之地。比起上一次的试探与不安，我更多了一丝稳重与熟练。心境、处境也都随着半个学期的过去而变得不同，半个学期中，身体上的，心理上的，太多的逆境让我变得步履维艰，曲曲折折，弯弯绕绕，我仿佛打不起精神，没有胃口，没有动力。感觉走的不顺畅的时候，支教这个旅程，给了我力量。自告奋勇承担起队长这一职务的我，从组织时的复杂和困难的经历，协调各种问题，从无到有，和校长和队
直返最高等级与直返APP：无需邀请码的返利新体验古楼
随着互联网的普及和电商的兴起，直返模式逐渐成为一种流行的商业模式。在这种模式下，消费者通过购买产品或服务，获得一定的返利，并可以分享给更多的人。其中，直返最高等级和直返APP是直返模式中的重要概念和工具。本文将详细介绍直返最高等级的概念、直返APP的使用以及与邀请码的关系。【高省】APP（高佣金领导者）是一个自用省钱佣金高，分享推广赚钱多的平台，百度有几百万篇报道，运行三年，稳定可靠。高省APP，
DIV+CSS+JavaScript技术制作网页（旅游主题网页设计与制作）云南大理 STU学生网页设计网页设计期末网页作业 html静态网页 html5期末大作业网页设计 web大作业
️精彩专栏推荐作者主页:【进入主页—获取更多源码】web前端期末大作业：【HTML5网页期末作业(1000套)】程序员有趣的告白方式：【HTML七夕情人节表白网页制作(110套)】文章目录二、网站介绍三、网站效果▶️1.视频演示2.图片演示四、网站代码HTML结构代码CSS样式代码五、更多源码二、网站介绍网站布局方面：计划采用目前主流的、能兼容各大主流浏览器、显示效果稳定的浮动网页布局结构。网站程
2020-04-12每天三百字之连接与替代冷眼看潮
不知道是不是好为人师，有时候还真想和别人分享一下我对某些现象的看法或者解释。人类社会不断发展进步的过程，就是不断连接与替代的过程。人类发现了火并应用火以后，告别了茹毛饮血的野兽般的原始生活（火烧、烹饪替代了生食）人类用石器代替了完全手工，工具的使用使人类进步一大步。类似这样的替代还有很多，随着科技的发展，有更多的原始的事物被替代，代之以更高效、更先进的技术。在近现代，汽车替代了马车，高速公路和铁路
探索OpenAI和LangChain的适配器集成：轻松切换模型提供商 nseejrukjhad langchain easyui 前端 python
#探索OpenAI和LangChain的适配器集成：轻松切换模型提供商##引言在人工智能和自然语言处理的世界中，OpenAI的模型提供了强大的能力。然而，随着技术的发展，许多人开始探索其他模型以满足特定需求。LangChain作为一个强大的工具，集成了多种模型提供商，通过提供适配器，简化了不同模型之间的转换。本篇文章将介绍如何使用LangChain的适配器与OpenAI集成，以便轻松切换模型提供商
利用Requests Toolkit轻松完成HTTP请求 nseejrukjhad http 网络协议网络 python
RequestsToolkit的力量：轻松构建HTTP请求Agent在现代软件开发中，API请求是与外部服务交互的核心。RequestsToolkit提供了一种便捷的方式，帮助开发者构建自动化的HTTP请求Agent。本文旨在详细介绍RequestsToolkit的设置、使用和潜在挑战。引言RequestsToolkit是一个强大的工具包，可用于构建执行HTTP请求的智能代理。这对于想要自动化与外
数组去重好奇的猫猫猫
整理自js中基础数据结构数组去重问题思考？如何去除数组中重复的项例如数组：[1,3,4,3,5]我们在做去重的时候，一开始想到的肯定是，逐个比较，外面一层循环，内层后一个与前一个一比较，如果是久不将当前这一项放进新的数组，挨个比较完之后返回一个新的去过重复的数组不好的实践方式上述方法效率极低，代码量还多，思考？有没有更好的方法这时候不禁一想当然有了！！！hashtable啊，通过对象的hash办法
春季养肝正当时 dxn悟
重温快乐2023年2月4日立春。春天来了，春暖花开，小鸟欢唱，那在这样的季节我们如何养肝呢？自然界的春季对应中医五行的木，人体五脏肝属木，“木曰曲直”，是以树干曲曲直直地向上、向外伸长舒展的生发姿态，来形容具有生长、升发、条达、舒畅等特征的食物及现象。根据中医天人相应的理念，肝五行属木，喜条达，主疏泄，与春天相应，所以春天最适合养肝。养肝首先要少生气，因为肝喜条达恶抑郁。人体五志肝为怒，生气发怒最
关于城市旅游的HTML网页设计——(旅游风景云南 5页)HTML+CSS+JavaScript 二挡起步 web前端期末大作业 javascript html css 旅游风景
⛵源码获取文末联系✈Web前端开发技术描述网页设计题材，DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业|游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作|HTML期末大学生网页设计作业，Web大学生网页HTML：结构CSS：样式在操作方面上运用了html5和css3，采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScrip
C/C++Win32编程基础详解视频下载择善Zach 编程 C++Win32
课题视频：C/C++Win32编程基础详解视频知识：win32窗口的创建 windows事件机制主讲：择善Uncle老师学习交流群：386620625 验证码：625 --
Guava Cache使用笔记 bylijinnan java guava cache
1.Guava Cache的get/getIfPresent方法当参数为null时会抛空指针异常我刚开始使用时还以为Guava Cache跟HashMap一样，get(null)返回null。实际上Guava整体设计思想就是拒绝null的，很多地方都会执行com.google.common.base.Preconditions.checkNotNull的检查。 2.Guava
解决ora-01652无法通过128（在temp表空间中） 0624chenhong oracle
解决ora-01652无法通过128（在temp表空间中）扩展temp段的过程一个sql语句后，大约花了10分钟，好不容易有一个结果，但是报了一个ora-01652错误，查阅了oracle的错误代码说明：意思是指temp表空间无法自动扩展temp段。这种问题一般有两种原因：一是临时表空间空间太小，二是不能自动扩展。分析过程：既然是temp表空间有问题，那当
Struct在jsp标签不懂事的小屁孩 struct
非UI标签介绍：控制类标签： 1：程序流程控制标签 if elseif else <s:if test="isUsed"> <span class="label label-success">True</span> </
按对象属性排序换个号韩国红果果 JavaScript 对象排序
利用JavaScript进行对象排序，根据用户的年龄排序展示 <script> var bob={ name;bob, age:30 } var peter={ name;peter, age:30 } var amy={ name;amy, age:24 } var mike={ name;mike, age:29 } var john={
大数据分析让个性化的客户体验不再遥远蓝儿唯美数据分析
顾客通过多种渠道制造大量数据，企业则热衷于利用这些信息来实现更为个性化的体验。分析公司Gartner表示，高级分析会成为客户服务的关键，但是大数据分析的采用目前仅局限于不到一成的企业。挑战在于企业还在努力适应结构化数据，疲于根据自身的客户关系管理（CRM）系统部署有效的分析框架，以及集成不同的内外部信息源。然而，面对顾客通过数字技术参与而产生的快速变化的信息，企业需要及时作出反应。要想实
java笔记4 a-john java
操作符 1，使用java操作符操作符接受一个或多个参数，并生成一个新值。参数的形式与普通的方法调用不用，但是效果是相同的。加号和一元的正号（+）、减号和一元的负号（-）、乘号（*）、除号（/）以及赋值号（=）的用法与其他编程语言类似。操作符作用于操作数，生成一个新值。另外，有些操作符可能会改变操作数自身的
从裸机编程到嵌入式Linux编程思想的转变------分而治之：驱动和应用程序 aijuans 嵌入式学习
笔者学习嵌入式Linux也有一段时间了，很奇怪的是很多书讲驱动编程方面的知识，也有很多书将ARM9方面的知识，但是从以前51形式的（对寄存器直接操作，初始化芯片的功能模块）编程方法，和思维模式，变换为基于Linux操作系统编程，讲这个思想转变的书几乎没有，让初学者走了很多弯路，撞了很多难墙。笔者因此写上自己的学习心得，希望能给和我一样转变
在springmvc中解决FastJson循环引用的问题 asialee 循环引用 fastjson
我们先来看一个例子： package com.elong.bms; import java.io.OutputStream; import java.util.HashMap; import java.util.Map; import co
ArrayAdapter和SimpleAdapter技术总结百合不是茶 android SimpleAdapter ArrayAdapter 高级组件基础
ArrayAdapter比较简单，但它只能用于显示文字。而SimpleAdapter则有很强的扩展性，可以自定义出各种效果 ArrayAdapter;的数据可以是数组或者是队列 // 获得下拉框对象 AutoCompleteTextView textview = (AutoCompleteTextView) this
九封信 bijian1013 人生励志
有时候，莫名的心情不好，不想和任何人说话，只想一个人静静的发呆。有时候，想一个人躲起来脆弱，不愿别人看到自己的伤口。有时候，走过熟悉的街角，看到熟悉的背影，突然想起一个人的脸。有时候，发现自己一夜之间就长大了。 2014，写给人
Linux下安装MySQL Web 管理工具phpMyAdmin sunjing PHP Install phpMyAdmin
PHP http://php.net/ phpMyAdmin http://www.phpmyadmin.net Error compiling PHP on CentOS x64 一、安装Apache 请参阅http://billben.iteye.com/admin/blogs/1985244 二、安装依赖包 sudo yum install gd
分布式系统理论 bit1129 分布式
FLP One famous theory in distributed computing, known as FLP after the authors Fischer, Lynch, and Patterson, proved that in a distributed system with asynchronous communication and process crashes,
ssh2整合(spring+struts2+hibernate)-附源码白糖_ eclipse spring Hibernate mysql 项目管理
最近抽空又整理了一套ssh2框架，主要使用的技术如下： spring做容器，管理了三层(dao,service,actioin)的对象 struts2实现与页面交互(MVC)，自己做了一个异常拦截器，能拦截Action层抛出的异常 hibernate与数据库交互 BoneCp数据库连接池，据说比其它数据库连接池快20倍，仅仅是据说 MySql数据库项目用eclipse
treetable bug记录 braveCS table
// 插入子节点删除再插入时不能正常显示。修改： //不知改后有没有错，先做个备忘 Tree.prototype.removeNode = function(node) { // Recursively remove all descendants of +node+ this.unloadBranch(node); // Remove
编程之美-电话号码对应英语单词 bylijinnan java 算法编程之美
import java.util.Arrays; public class NumberToWord { /** * 编程之美电话号码对应英语单词 * 题目： * 手机上的拨号盘，每个数字都对应一些字母，比如2对应ABC，3对应DEF.........，8对应TUV，9对应WXYZ， * 要求对一段数字，输出其代表的所有可能的字母组合
jquery ajax读书笔记 chengxuyuancsdn jQuery ajax
1、jsp页面 <%@ page language="java" import="java.util.*" pageEncoding="GBK"%> <% String path = request.getContextPath(); String basePath = request.getScheme()
JWFD工作流拓扑结构解析伪码描述算法 comsci 数据结构算法工作活动 J#
对工作流拓扑结构解析感兴趣的朋友可以下载附件，或者下载JWFD的全部代码进行分析 /* 流程图拓扑结构解析伪码描述算法 public java.util.ArrayList DFS(String graphid, String stepid, int j)
oracle I/O 从属进程 daizj oracle
I/O 从属进程　　I/O从属进程用于为不支持异步I/O的系统或设备模拟异步I/O.例如，磁带设备(相当慢)就不支持异步I/O.通过使用I/O 从属进程，可以让磁带机模仿通常只为磁盘驱动器提供的功能。就好像支持真正的异步I/O 一样，写设备的进程(调用者)会收集大量数据，并交由写入器写出。数据成功地写出时，写入器(此时写入器是I/O 从属进程，而不是操作系统)会通知原来的调用者，调用者则会
高级排序:希尔排序 dieslrae 希尔排序
public void shellSort(int[] array){ int limit = 1; int temp; int index; while(limit <= array.length/3){ limit = limit * 3 + 1;
初二下学期难记忆单词 dcj3sjt126com english word
kitchen 厨房 cupboard 厨柜 salt 盐 sugar 糖 oil 油 fork 叉；餐叉 spoon 匙；调羹 chopsticks 筷子 cabbage 卷心菜；洋白菜 soup 汤 Italian 意大利的 Indian 印度的 workplace 工作场所 even 甚至；更 Italy 意大利 laugh 笑 m
Go语言使用MySQL数据库进行增删改查 dcj3sjt126com mysql
目前Internet上流行的网站构架方式是LAMP，其中的M即MySQL, 作为数据库，MySQL以免费、开源、使用方便为优势成为了很多Web开发的后端数据库存储引擎。MySQL驱动Go中支持MySQL的驱动目前比较多，有如下几种，有些是支持database/sql标准，而有些是采用了自己的实现接口,常用的有如下几种: http://code.google.c...o-mysql-dri
git命令 shuizhaosi888 git
---------------设置全局用户名： git config --global user.name "HanShuliang" //设置用户名 git config --global user.email "[email protected]" //设置邮箱 ---------------查看环境配置 git config --li
qemu-kvm 网络 nat模式 (四) haoningabc kvm qemu
qemu-ifup-NAT #!/bin/bash BRIDGE=virbr0 NETWORK=192.168.122.0 GATEWAY=192.168.122.1 NETMASK=255.255.255.0 DHCPRANGE=192.168.122.2,192.168.122.254 TFTPROOT= BOOTP= function check_bridge()
不要让未来的你，讨厌现在的自己 jingjing0907 生活奋斗工作梦想
故事one 　23岁，他大学毕业，放弃了父母安排的稳定工作，独闯京城，在家小公司混个小职位，工作还算顺手，月薪三千，混了混，混走了一年的光阴。　　　　24岁，有了女朋友，从二环12人的集体宿舍搬到香山民居，一间平房，二人世界，爱爱爱。偶然约三朋四友，打扑克搓麻将，日子快乐似神仙；　　　　25岁，出了几次差，调了两次岗，薪水涨了不过百，生猛狂飙的物价让现实血淋淋，无力为心爱银儿购件大牌
枚举类型详解一路欢笑一路走 enum 枚举详解 enumset enumMap
枚举类型详解一.Enum详解 1.1枚举类型的介绍 JDK1.5加入了一个全新的类型的”类”—枚举类型，为此JDK1.5引入了一个新的关键字enum,我们可以这样定义一个枚举类型。 Demo:一个最简单的枚举类 public enum ColorType { RED
第11章动画效果（上） onestopweb 动画
index.html <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xmlns="http://www.w3.org/
Eclipse中jsp、js文件编辑时，卡死现象解决汇总 ljf_home eclipse jsp卡死 js卡死
使用Eclipse编辑jsp、js文件时，经常出现卡死现象，在网上百度了N次，经过N次优化调整后，卡死现象逐步好转，具体那个方法起到作用，不太好讲。将所有用过的方法罗列如下： 1、取消验证 windows–>perferences–>validation 把除了manual 下面的全部点掉，build下只留 classpath dependency Valida
MySQL编程中的6个重要的实用技巧 tomcat_oracle mysql
每一行命令都是用分号(;)作为结束对于MySQL，第一件你必须牢记的是它的每一行命令都是用分号(;)作为结束的，但当一行MySQL被插入在PHP代码中时，最好把后面的分号省略掉，例如： mysql_query("INSERT INTO tablename(first_name,last_name)VALUES('$first_name',$last_name')");
zoj 3820 Building Fire Stations(二分+bfs) 阿尔萨斯 Build
题目链接：zoj 3820 Building Fire Stations 题目大意：给定一棵树，选取两个建立加油站，问说所有点距离加油站距离的最大值的最小值是多少，并且任意输出一种建立加油站的方式。解题思路：二分距离判断，判断函数的复杂度是o(n)，这样的复杂度应该是o(nlogn)，即使常数系数偏大，但是居然跑了4.5s，也是醉了。判断函数里面做了3次bfs，但是每次bfs节点最多