Deformable ConvNets v2 Pytorch版源码讲解_2
接着上一章的来讲,上一章主要是介绍了一下可变形卷积v1和v2,红色字都是基于源码来的。那么这一篇文章就分析一下整个代码流程是怎么样的。代码是Pytorch版的,这里附上Github地址:https://github.com/4uiiurz1/pytorch-deform-conv-v2/blob/master/deform_conv_v2.py。这里再次感谢大佬的开源代码!
先附上我debug时采用的代码。
if __name__ == '__main__':
feature_map = torch.randint(high=256, size=(1, 2, 5, 5), dtype=torch.float32)
feature_map = feature_map/255
deformconv2d = DeformConv2d(2, 4, modulation=True)
output = deformconv2d(feature_map)
print(output.shape)我模拟了网络中间的特征图输入,即[1,2,5,5](Batch_size=1,Channel=2,H,W=5)。同时进行了归一化操作,然后我初始化了一个可变形卷积,其输入通道数等于上一层的通道即2,输出通道数为4,最后利用forward前传得出output,output最终的输出为[1,4,5,5]。
class DeformConv2d(nn.Module):
def __init__(self, inc, outc, kernel_size=3, padding=1, stride=1, bias=None, modulation=False):
"""
Args:
modulation (bool, optional): If True, Modulated Defomable Convolution (Deformable ConvNets v2).
"""
super(DeformConv2d, self).__init__()
self.kernel_size = kernel_size
self.padding = padding
self.stride = stride
self.zero_padding = nn.ZeroPad2d(padding)
self.conv = nn.Conv2d(inc, outc, kernel_size=kernel_size, stride=kernel_size, bias=bias)
self.p_conv = nn.Conv2d(inc, 2*kernel_size*kernel_size, kernel_size=3, padding=1, stride=stride)
nn.init.constant_(self.p_conv.weight, 0)
self.p_conv.register_backward_hook(self._set_lr)
self.modulation = modulation
if modulation:
self.m_conv = nn.Conv2d(inc, kernel_size*kernel_size, kernel_size=3, padding=1, stride=stride)
nn.init.constant_(self.m_conv.weight, 0)
self.m_conv.register_backward_hook(self._set_lr)首先分析下其初始化函数,self.conv代表的是最终在offset过后的特征图上进行卷积的那个卷积核参数设置,注意它的stride=kernel_size。它不是写错了。self.p_conv就是学习到的offset,他得到的是[1,2*3*3,5,5]大小的Tensor。通道2*3*3就是原论文中的2N!这里我简单的解释下2N的含义,让大家先有个初步的认识。。那么2N是怎么来的。这里上一张图
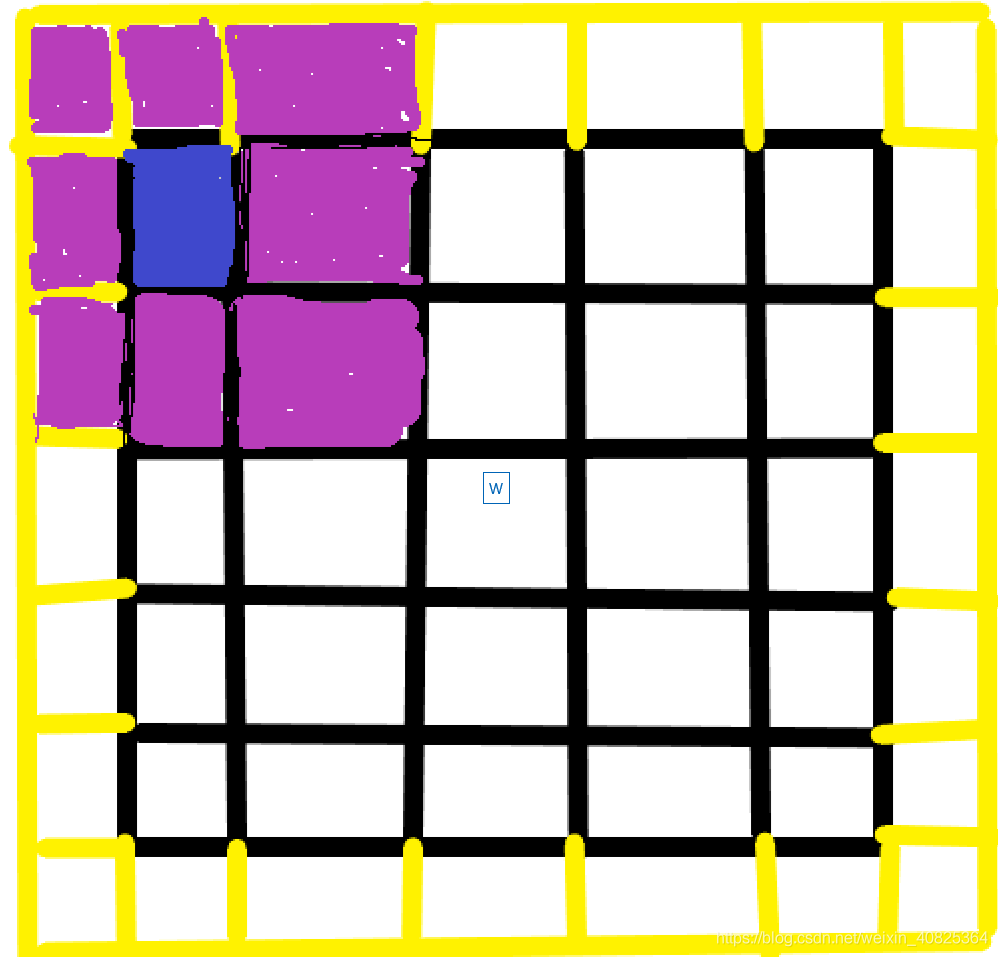
图1
图画的有点丑了。解释一下我这个图,黑色的矩形框就是咱们的原图(5*5大小),粉红色是咱们的3*3的卷积核,黄色是因为我们有一个padding=1的操作,现在试想一个正常的卷积操作。当粉红色卷积核在原图上滑动过程第一次就是如上图所示,但是因为咱们这是可变形卷积。也就是这8个粉红色的点加上这个蓝色的点即原图上的卷积采样点都要学习一组offset的,一共9组offset。每一组offset都有x偏移和y偏移总共18个offset。同时这18个offset是由卷积采样点中心负责学习,一共有25个卷积采样中心点,为什么是25?建议画图模拟卷积每次滑动过程,你在看每次滑动窗口的中心,你就会发现每一个卷积采样中心点都是图中黑色小矩形框。故这里得到的是[1,2*3*3,5,5]大小的Tensor。
def forward(self, x):
offset = self.p_conv(x)
if self.modulation:
m = torch.sigmoid(self.m_conv(x))
dtype = offset.data.type()
ks = self.kernel_size
N = offset.size(1) // 2
if self.padding:
x = self.zero_padding(x)
# (b, 2N, h, w)
p = self._get_p(offset, dtype)接下来我们看其forward函数。首先利用offset学习到一个偏移量Tensor,形状为(1,18,5,5).modulation为是否给这些offset后的像素值都学习一个权重。我设置的是True.那么这里会学习到一个权重,形状为[1,9,5,5]。同时将其sigmoid激活成一个0-1的正小数。self.padding的含义是是否将其全零填充。我这里默认是padding等于1的。所以此时x的大小不是[5,5]了,而是[7,7]。后来就到了self._get_p()函数了。其实这个函数就是在复现论文里的这个公式。
图2
def _get_p(self, offset, dtype):
N, h, w = offset.size(1)//2, offset.size(2), offset.size(3)
# (1, 2N, 1, 1)
p_n = self._get_p_n(N, dtype)
# (1, 2N, h, w)
p_0 = self._get_p_0(h, w, N, dtype)
p = p_0 + p_n + offset
return p简单说明一下p_n,p_0是什么,p_0就是一个3*3卷积核在输入特征图上进行采样的3*3区域的中心点,可观察到图1中所有的黑色小矩形框就是一个p_0,如下图所示。
图3
p_n是每一个采样中心点的九个值的偏移量,可能有点抽象。咱们打印出来看下
p_n = [[[[-1.]],[[-1.]],[[-1.]],[[ 0.]],[[ 0.]],[[ 0.]],[[ 1.]],[[ 1.]],[[ 1.]],
[[-1.]],[[ 0.]],[[ 1.]],[[-1.]],[[ 0.]],[[ 1.]],[[-1.]],[[ 0.]],[[ 1.]]]] shape=(1,18,1,1) 前9个是x偏移,后9个是y偏移。一一对应为一组。得出的这9个点就是(x-1,y-1),(x-1,y),(x-1,y+1),(x,y-1),(x,y),(x,y+1),(x+1,y-1),(x+1,y),(x+1,y+1)吗?这9个点不就是以(x,y)为中心的卷积核采样区域吗?
p_0 = [[[[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5.]],
[[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5.]],
[[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5.]],
[[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5.]],
[[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5.]],
[[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5.]],
[[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5.]],
[[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5.]],
[[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.]],
[[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.]],
[[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.]],
[[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.]],
[[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.]],
[[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.]],
[[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.]],
[[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.]],
[[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.]]]] shape=(1,18,5,5) 这里同上面一样,九个为一组,前面是x,后面是y。将xy一一对应组合起来就是每一个p_0。那么如果运算p_0+p_n得到的就是下面这个Tensor
p_0+p_n:
[[[[0., 0., 0., 0., 0.],
[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.]],
[[0., 0., 0., 0., 0.],
[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.]],
[[0., 0., 0., 0., 0.],
[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.]],
[[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5.]],
[[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5.]],
[[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5.]],
[[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5.],
[6., 6., 6., 6., 6.]],
[[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5.],
[6., 6., 6., 6., 6.]],
[[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5.],
[6., 6., 6., 6., 6.]],
[[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.]],
[[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.]],
[[2., 3., 4., 5., 6.],
[2., 3., 4., 5., 6.],
[2., 3., 4., 5., 6.],
[2., 3., 4., 5., 6.],
[2., 3., 4., 5., 6.]],
[[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.]],
[[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.]],
[[2., 3., 4., 5., 6.],
[2., 3., 4., 5., 6.],
[2., 3., 4., 5., 6.],
[2., 3., 4., 5., 6.],
[2., 3., 4., 5., 6.]],
[[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.]],
[[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.],
[1., 2., 3., 4., 5.]],
[[2., 3., 4., 5., 6.],
[2., 3., 4., 5., 6.],
[2., 3., 4., 5., 6.],
[2., 3., 4., 5., 6.],
[2., 3., 4., 5., 6.]]]] shape =(1,18,5,5) 我们单独挑2组来说,
[[0., 0., 0., 0., 0.], [[0., 1., 2., 3., 4.],
[1., 1., 1., 1., 1.], [0., 1., 2., 3., 4.],
[2., 2., 2., 2., 2.], [0., 1., 2., 3., 4.],
[3., 3., 3., 3., 3.], [0., 1., 2., 3., 4.],
[4., 4., 4., 4., 4.]] [0., 1., 2., 3., 4.]] 这一组分别是[1,0,5,5]和[1,9,5,5],他们的x,y是分别对应的。一个25个坐标值,分别是(0,0),(0,1),(0,2).......(4,0),(4,1),(4,2),(4,3),(4,4)这些点。建议读者这里自己画个图,你会发现这些点就是每个卷积采样区域的9个点中左上角的点的集合。同理我们分析另外一组。
[[2., 2., 2., 2., 2.], [[2., 3., 4., 5., 6.],
[3., 3., 3., 3., 3.], [2., 3., 4., 5., 6.],
[4., 4., 4., 4., 4.], [2., 3., 4., 5., 6.],
[5., 5., 5., 5., 5.], [2., 3., 4., 5., 6.],
[6., 6., 6., 6., 6.]] [2., 3., 4., 5., 6.]] 这一组分别是[1,8,5,5]和[1,17,5,5],一共25个坐标值,分别是(2,2),(2,3),(2,4),(2,5),(2,6)........(6,2),(6,3),(6,4),(6,5),(6,6)这些点就是每个卷积采样区域的9个点钟右下角的点的集合。同理你可以对其他组进行同样的分析。这里不再赘述。
那么分析完了p_0+p_n,那么最终加上offset。就得出了这里所有卷积采样点的一个偏移。那么我在这里有一个猜想。我说过offset的偏移量shape是(1,18,5,5)的Tensor的。这个Tensor的[1,0,5,5]其实是对应所有卷积采样点中左上角坐标点的x偏移,[1,9,5,5]其实是对应着所有卷积采样点中左上角坐标点的y偏移。同理[1,8,5,5]和[1,17,5,5]是对应着右下角坐标点的x,y偏移的。我这个猜想应该是对的。不然他们怎么能相加还能对应上呢?如果你有不同的看法我们可以一起讨论。
到此为止,咱们其实完成了一个工作就是对每个卷积采样区域都学习到了一组offset,但这些offset是存在小数的,这些小数是不能直接取整的,举个例子我为(0,0)这个坐标点学习到了一组offset为(0.2,0.3),那么offset后这个坐标点为(0+0.2,0+0.3)=(0.2,0.3)。你如果直接取整得出的还是(0,0)。你做的其实是一个恒等映射即y=x,那么你学习的效果就大打折扣。这点是我的理解。所以咱们得到了offset后应该用双线性插值来计算该点的特征值。