一文全解梯度下降法
一句话总结梯度下降:
通过寻找损失最小值,来学习到最优的模型参数
据我所知,几乎所有常见的深度神经网络都会用梯度下降来更新模型的参数,参数学习的越好就说明它越拟合我们的训练数据,越拟合训练数据说明机器学习的成绩越好,我们再用它来预测新数据的时候,得到的效果就越好。
笔记文,文章末尾有个视频链接
说实话,在我学习它这个视频之前,我就知道上面的概念,不过对于经常调库的我来说也够用了,下面是我针对原作者视频中的知识点再加上我的个人理解总结的梯度下降法的完整流程,我觉得特别简单明了,也让我轻松掌握了有关梯度下降的基本原理
梯度下降的完整流程:
1.定义损失函数、
2.选择一个参数起始点、
3.计算梯度下降的方向、
4.沿着这个方向按照学习率前进,
5.重复第3第4步直到找到最优参数
以线性回归问题为例说明这个流程:
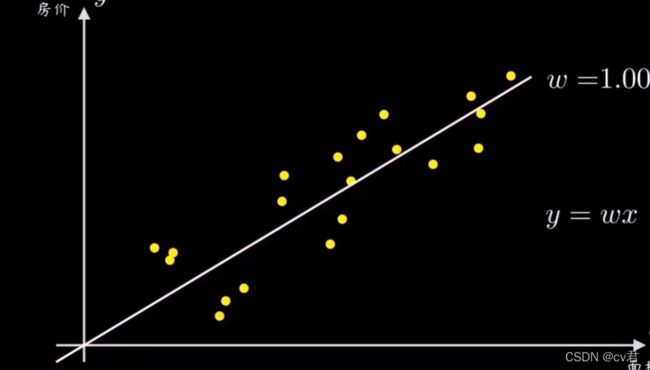
过原点的直线 y=wx 就相当于线性回归问题中用于做预测的函数,y是房价,x是面积,每个样本代表不同面积的具体房价
机器的任务就是想办法计算出一条最好的直线来拟合这些样本点数据,而直线的斜率w就可以简单控制直线,所以我们的目的是要求解出最能拟合数据分布的变量w
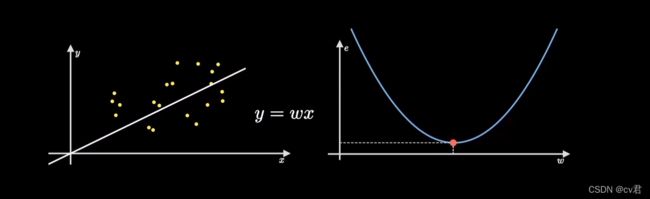
为了方便求解出最优参数w,我们引入了与这条直线相关的损失函数
我们通过预测函数和误差公式推导出损失函数,成功的将直线拟合样本点的过程映射到了一个损失函数上,并且它是个开口向上的抛物线图像,它是以参数w为自变量、误差或者损失值作为因变量的,见下图中的右侧图
因为我们的目标是拟合出最接近这些数据分布的直线,也就是找到使得误差代价最小的参数w,对应在右图的损失函数图像上就是它的最低点,这个不断寻找最低点的过程就是梯度下降要干的活。
我们先随机选取一个参数起始点,对应到曲线上的某个误差值,然后不断的沿着损失函数曲线陡峭程度最大的方向前进,就能更快更准的找到误差的最低点。
这个陡峭程度就是梯度,它是损失函数的导数,对于抛物线而言就是曲线的斜率
另外,因为梯度的方向是损失函数值增加最快的方向,负梯度是损失函数值下降最快的方向,所以我们其实是沿着梯度的反方向前往最低点。这就是为何叫梯度下降的原因
确定了损失函数值的下降方向以后,还需要考虑前进的步长,即学习率
学习率是步长超参数,人为选择,选择学习率时,步子太大即选择数值太大会反复横跳,步子太小会走得很慢浪费计算
上面我们是用线性回归做预测函数的,实际情况中房价不仅与面积,还与城市、地段、政策等相关,那么预测函数就会是非线性甚至是曲面多维的各种复杂函数,对应的损失函数也可能是更复杂的,如
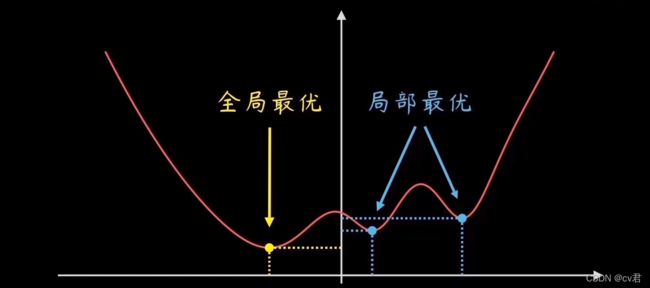
这个损失函数是波浪曲线,在机器学习过程中可能陷入到学习到局部最优参数却不知还有更优的参数,不过不用担心,现在很多调整学习率的方法都会尽力避免这个问题,如Adam、Mumontum等,只要会调库就行了,具体哪个更适合得你们自己去看啦
无论是对哪种损失函数求最低点,沿着梯度的反方向前进,最终都能走到最低点
上面说了梯度下降的原理,但是实际我们很少直接使用梯度下降,因为我们每次计算梯度时要对每个损失函数求导,这个损失函数是对所有训练样本的平均损失,意味着每次计算梯度都要计算一遍所有样本,花费的时间成本太大了。现在深度学习默认使用的是小批量随机梯度下降方法来训练模型得到最优参数
另外,小批量batchsize也是个超参数, 它选择越小,对收敛越好,即模型拟合数据的越好;对了,上述那个例子中的直线或者说预测函数 y=wx 就可以看作是简单的预测模型,所以才总说训练模型的参数嘛
batchsize选择越小,产生的噪音越多,噪音对神经网络是有一定好处的,深度神经网络太复杂了,一定的噪音可以避免网络模型在训练的时候不会走偏;也就是说模型对各种噪音的容忍度越好,则模型的泛化性就越好,泛化性越好就能让模型更好预测其他新数据
当然,选择太小也不行,会浪费计算,时间成本高啊;batchsize选择太大会虽然导致收敛问题,但只要不是特别大,最后多花点时间还是能收敛的。
小批量随机梯度下降中的‘随机’是随机采样的意思,批量大小都是提前定义好的;假如batchsize是128,那么随机从所有样本中采样128个读进内存用于训练
视频链接:【梯度下降】是什么鬼?(可视化讲解 高中生都说懂)_哔哩哔哩_bilibili
cv君 微信,上百份深度学习数据+教学+技术交流+千人交流群