【典例】二叉树递归结构经典题目合集@二叉树

小边有话要说呢：这些题目都是对于二叉树递归遍历结构的理解运用，都是非常经典的题目。
做几道就会有感觉，目前看所有题目都跑不掉的，递归不过就是，处理当前节点 - 可能是做一些操作/可能是做一些判断往往是跳出条件，然后就是递归左子树、递归右子树(注：前中后序应题目而变)，and空节点往往也是递归跳出处。
递归好像是难想，起码三个月前初学我不画递归展开图有地方就是晕晕的，到现在直接在脑子里递，还是有一点进步的，做几道就有感觉了。不过递归的时间复杂度啊，有时可以进行一些优化，它们都写在文章里了，这是我还需要继续修炼的。

正文开始@小边同学还爱编程吗

Always

1. 单值二叉树

1.1 题目

题目链接：单值二叉树

1.2 思路及题解

分治：

• 单值二叉树 = root和左右孩子的值相等 + 左子树是单值二叉树 + 右子树是单值二叉树
• 有答案的最小子问题：空节点； root和左右孩子的值不等

bool isUnivalTree(struct TreeNode* root){
    if(root == NULL)
        return true;
    
    if(root->left && root->left->val != root->val)
        return false;

    if(root->right && root->right->val != root->val)
        return false;

    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

2. 相同二叉树

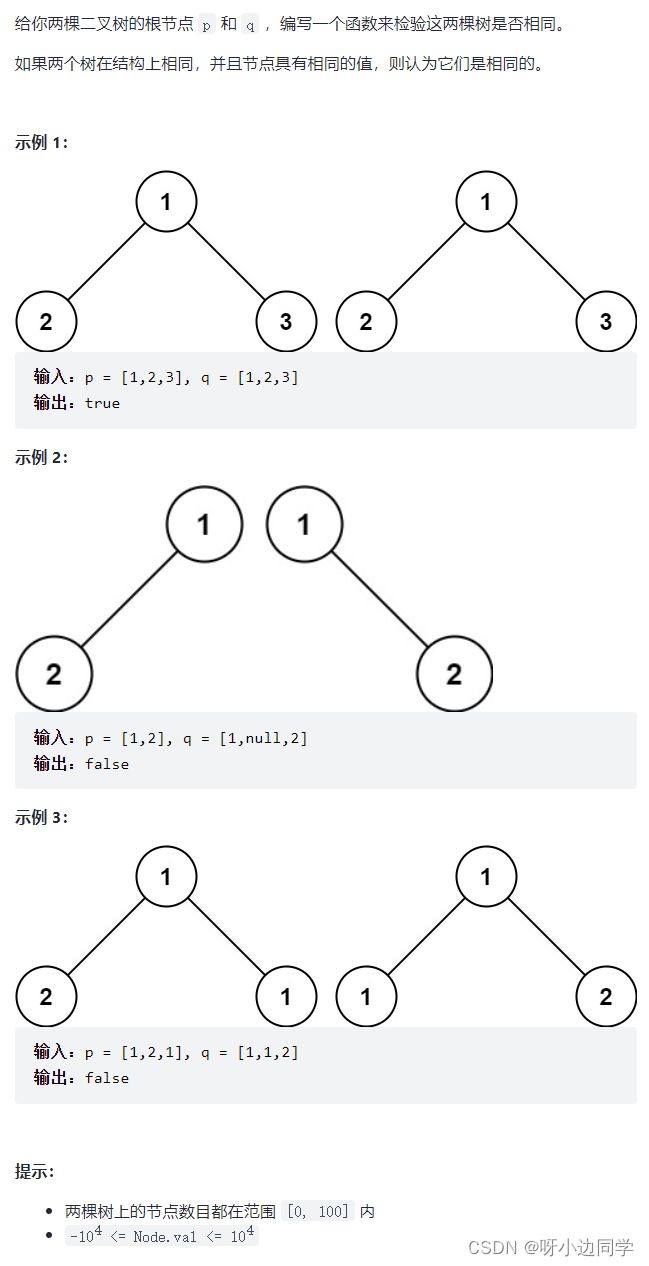
2.1 题目

题目链接：相同的树

2.2 思路及题解

分治：

• 相同二叉树 = 比较两棵树的根 + 递归左子树（两棵树的左子树是否是相同二叉树）+ 递归右子树（两棵树的右子树是否是相同二叉树）

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p == NULL && q == NULL)
        return true;

    if(p == NULL || q == NULL)
        return false; // 能走到这里则p和q中一定有一个为空
	
    // 能走到这里说明p和q一定都不为空
    if(p->val != q->val)
        return false;

    return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}

这道题目一定要理解好，后面的镜像二叉树就是它一个小变形；判断是否是另一棵树的子树，也需要它来做子函数来判断是否相等。

3. 镜像二叉树

3.1 题目

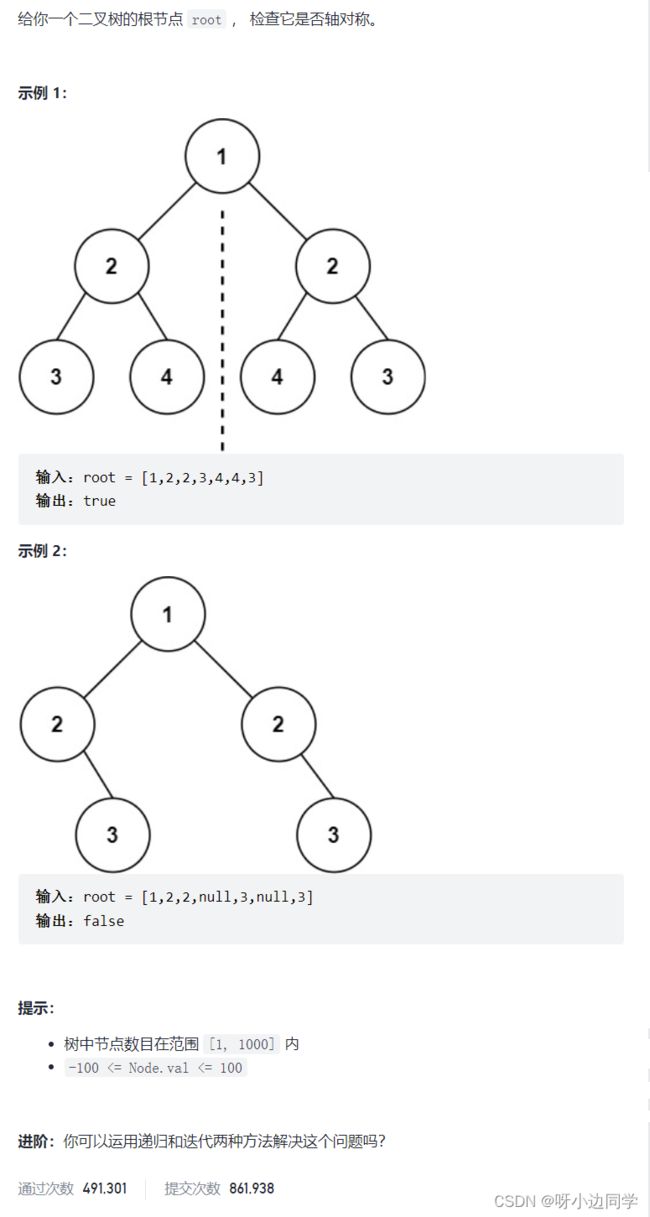
题目链接：对称二叉树

3.2 思路及题解

是否是镜像二叉树，实际上就是要比较左右两棵子树是否对称。你能否感受到，这和上一题是否为相同二叉树很像，只不过这里是比较对称节点是否相同罢了。

在原本的函数接口上我们是递归不起来的，因此要写一个子函数。这个子函数就是相同二叉树的小变形。

bool _isSymmetric(struct TreeNode* p, struct TreeNode* q){
    if(p == NULL && q == NULL)
        return true;

    if(p == NULL || q == NULL)
        return false;
    
    if(p->val != q->val)
        return false;
    
    return _isSymmetric(p->right, q->left) && _isSymmetric(p->left,q->right);
}

bool isSymmetric(struct TreeNode* root){
    if(root == NULL)
        return true;

    return _isSymmetric(root->left,root->right);
}

4. 另一棵树的子树

4.1 题目

题目链接：另一棵树的子树

4.2 思路及题解

用root的每一个子树都和sub比一下。 这里同样会用到判断相同二叉树这个子函数。

分治：

• 当前节点的子树与subTree相同吗 + 递归左子树 + 递归右子树
• 递归终止条件：当前节点的子树与subTree相同，则说明存在子树

bool _isSubtree(struct TreeNode* p, struct TreeNode* q){
    if(p == NULL && q == NULL)
        return true;

    if(p == NULL || q == NULL)
        return false;

    if(p->val != q->val)
        return false;
    
    return _isSubtree(p->left,q->left) && _isSubtree(p->right,q->right);
}


bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    // 找到了
    if(_isSubtree(root,subRoot))
        return true;

    if(root->left && isSubtree(root->left,subRoot))
        return true;
    if(root->right && isSubtree(root->right,subRoot))
        return true;
        
    return false;
}

时间复杂度分析：假设规模都是N

计算递归的时间复杂度，公式是 递归次数*每次递归调用次数，注意思想计算。

• 最好情况的时间复杂度是多少？O(N).

1. 一进来就相等
2. 每个子树的根就不相等，就比较了N次根

• 最坏情况的时间复杂度是多少？O(N^2)

root的每个子树跟subRoot都要比一次，isSameTree每次都比较到最后一个节点才不相同。

也可以这样写 ——

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
   if(root == NULL)
        return false;
        
    //找到了 
    if(isSameTree(root,subRoot))
        return true;
    
    return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}

4.3 反思

这与查找值为x的节点非常类似。

它们都是，先跟当前节点比，相等了就返回；不相等则去左树去找，左树找到了，就返回，如果左树没找到，再去右树找。只不过在这里比较的不是一个值，而是root的子树，调用一个函数来比较。是一个更复杂的查找问题。

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;

	//递归不要把返回值丢了，而且要注意效率
	BTNode* leftRet = BinaryTreeFind(root->left, x);
	if (leftRet)
		return leftRet;

	BTNode* rightRet = BinaryTreeFind(root->right, x);
	if (rightRet)
		return rightRet;

	return NULL;  
}

5. 翻转二叉树

5.1 题目

题目链接：翻转二叉树

5.2 思路和题解

其实啊，这个树的递归结构做多了除了有经验，还是有感觉的。

分治：

• 翻转二叉树 = 翻转当前节点左右链 + 递归左子树（翻转左子树） + 递归右子树（翻转右子树）
• 不可拆分的子问题：空节点

struct TreeNode* invertTree(struct TreeNode* root){
    if(root == NULL)
        return NULL;
    
    struct TreeNode* tmp = root->left;
    root->left = root->right;
    root->right = tmp;
    
    invertTree(root->left);
    invertTree(root->right);
    return root;
}

6. 平衡二叉树

6.1 题目

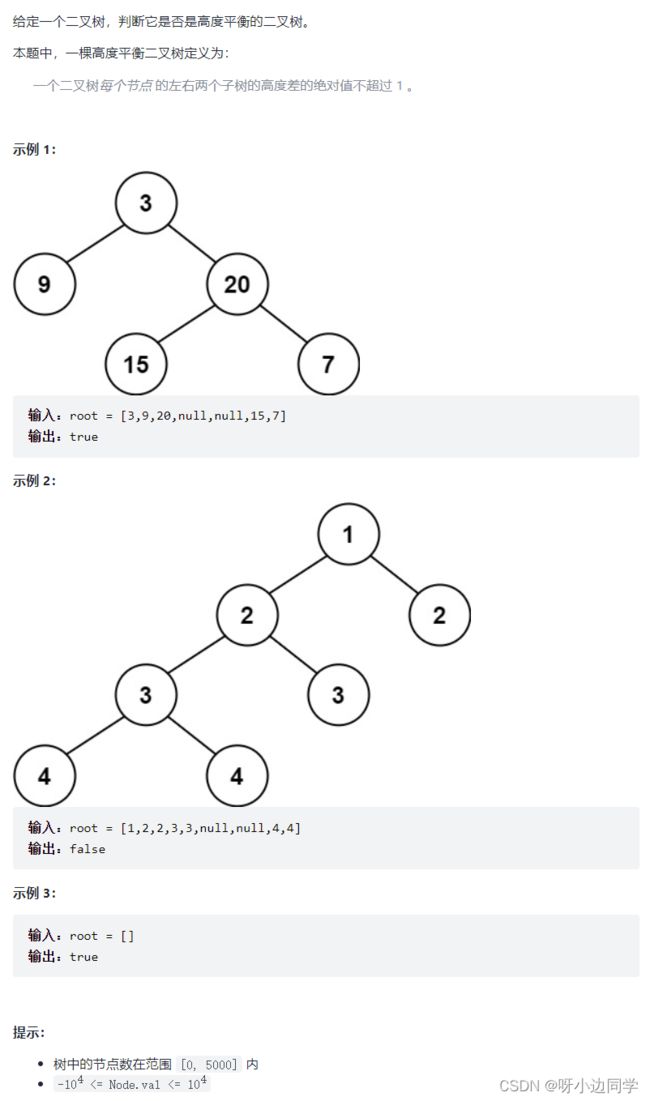
题目链接：平衡二叉树

6.2 思路和题解

分治：自顶向下

int TreeDepth(struct TreeNode* root)
{
    if(root == NULL)
        return 0;
    int leftDepth = TreeDepth(root->left);
    int rightDepth = TreeDepth(root->right);
    return 1 + (leftDepth > rightDepth ? leftDepth:rightDepth);
}

bool isBalanced(struct TreeNode* root){
    if(root == NULL)
        return true;

    int gap = abs(TreeDepth(root->left)-TreeDepth(root->right));
    if(gap > 1)
        return false;
    
    return isBalanced(root->left) && isBalanced(root->right);
}

时间复杂度分析 $O(N^2)$

递归的时间复杂度 = 递归次数 * 递归调用次数

• 递归次数：isBalance最坏情况遍历所有节点$N$
• 递归中调用次数：求树的高度TreeDepth最坏情况，树退化为链式结构$N$

优化：后序判断 - 自底向上

时间复杂度：$O(N)$

bool _isBalanced(struct TreeNode* root, int* ph)
{
	if (root == NULL)
	{
		*ph = 0;//空树返回高度为0
		return true;
	}
    
	//先判断左子树，再判断右子树
	int leftHight = 0;
	if (_isBalanced(root->left, &leftHight) == false)
		return false;

	int rightHight = 0;
	if (_isBalanced(root->right, &rightHight) == false)
		return false;

	// 把当前树的高度带给上一层的父亲
	*ph = fmax(leftHight, rightHight) + 1;

	return abs(leftHight - rightHight) < 2;//平衡二叉树的条件
}

bool isBalanced(struct TreeNode* root)
{
	int hight = 0;
	return _isBalanced(root, &hight);
}

7. 二叉树的前中后序遍历

题目链接：二叉树的前序遍历
题目链接：二叉树的中序遍历
题目链接：二叉树的后序遍历

这里的前中后序与我们自己写的有一点小变化，因此单拿出来。主要谈一下前序，中序后序那就是一样的。

它要求把前序遍历存入数组中，数组是malloc来的。

注意：

• 输出型参数：Leetcode上要返回数组，不知道数组有多大，返回值又不允许多个。把一个外边某个变量的地址传给你，解引用赋值，让外边拿到
• 数组开多大？计算节点个数，直接一次性开好。
• 它给的这个接口递归不起来（你每次都开一个数组吗？），自己写一个子函数（前面加一个_是命名习惯）
• 递归中，注意，要对同一个i++。上篇文章中，在谈求树的节点的个数时，就强调过这个问题了。

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

int TreeSize(struct TreeNode* root)
{
    if(root == 0)
        return 0;
    return 1 + TreeSize(root->left) + TreeSize(root->right);
}

void _preorderTraversal(struct TreeNode* root,int* a,int* pi){
    if(root == NULL)
        return ;
    // 依次放入数组a中
    a[*pi] = root-> val;
    (*pi)++;
    _preorderTraversal(root->left, a, pi);
    _preorderTraversal(root->right, a, pi);
}

int* preorderTraversal(struct TreeNode* root, int* returnSize){
    int size = TreeSize(root);
    *returnSize = size;
    int* a = (int*)malloc(size*sizeof(int));
    int i = 0;
    _preorderTraversal(root, a, &i);
    return a;
}

中序&后序要注意的问题都是一样的。

中序遍历 ——

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int TreeSize(struct TreeNode* root)
{
    if(root == NULL)
        return 0;
    return 1 + TreeSize(root->left) + TreeSize(root->right);
}

void _inorderTraversal(struct TreeNode* root, int* a,int* pi)
{
    if(root == NULL)
        return ;
    _inorderTraversal(root->left, a, pi);
    a[*pi] = root->val;
    (*pi)++;
    _inorderTraversal(root->right, a, pi);
}

int* inorderTraversal(struct TreeNode* root, int* returnSize){
    int size = TreeSize(root);
    *returnSize = size;
    int* a = (int*)malloc(size*sizeof(int));
    int i = 0;
    _inorderTraversal(root, a, &i);
    return a;
}

后序遍历 ——

int TreeSize(struct TreeNode* root)
{
    if(root == NULL)
        return NULL;
    return 1 + TreeSize(root->left) + TreeSize(root->right);
}

void _postorderTraversal(struct TreeNode* root, int* a,int* pi)
{
    if(root == NULL)
        return ;
    _postorderTraversal(root->left, a, pi);
    _postorderTraversal(root->right, a, pi);
    a[*pi] = root->val;
    (*pi)++;
}

int* postorderTraversal(struct TreeNode* root, int* returnSize){
    int size = TreeSize(root);
    *returnSize = size;
    int* a = (int*)malloc(size*sizeof(int));
    int i = 0;
    _postorderTraversal(root, a, &i);
    return a;
}

8. 二叉树的构建和遍历THU

8.1 题目

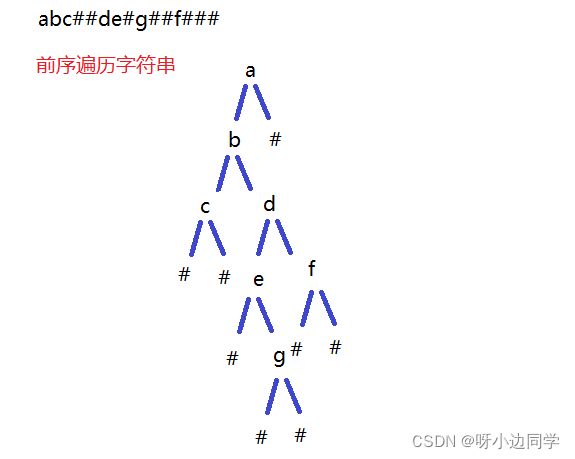
题目链接：二叉树的构建和遍历TsingHua

8.2 思路和题解

• 前序遍历字符串，递归建立二叉树
• 中序打印输出
• 后序销毁

前中后序凑齐了，真是妙呢！

注：构建二叉树时，遍历字符串还是用到了输出型参数，应该很熟悉了。构建的树是通过返回值带回来了的，就不用传二级指针了，你看好多题目的接口就是这样的，比如上面的翻转二叉树。

#include
#include
#include

typedef struct TreeNode
{
    char val;
    struct TreeNode* left;
    struct TreeNode* right;
}TreeNode;

TreeNode* CreateTree(char* str,int* pi)
{
    if(str[*pi] == '#')
    {
        (*pi)++;
        return NULL;
    }
    TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
    root->val = str[*pi];
    (*pi)++;
    root->left = CreateTree(str, pi);
    root->right = CreateTree(str, pi);
    return root;
}

void inorderTraversal(TreeNode* root)
{
    if(root == NULL)
        return ;
    inorderTraversal(root->left);
    printf("%c ",root->val);
    inorderTraversal(root->right);
}

void DestroyTree(TreeNode* root)
{
    if(root == NULL)
        return ;
    DestroyTree(root->left);
    DestroyTree(root->right);
    free(root);
}

int main()
{
    char str[100];
    scanf("%s",str);
    int i = 0;
    TreeNode* root = CreateTree(str, &i);
    inorderTraversal(root);
    DestroyTree(root);
    root = NULL;
    return 0; 
}