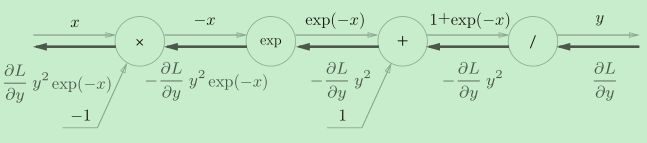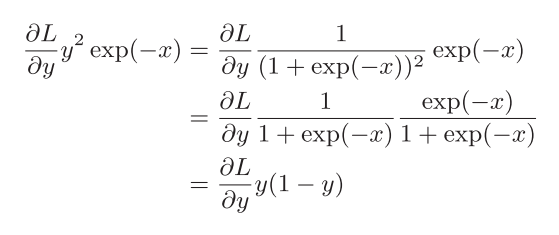动手实现深度神经网络3 增加误差反向传播计算梯度&完成MNIST数据集手写数字识别
动手实现深度神经网络3 增加误差反向传播计算梯度
在这一部分中我们利用误差反向传播来计算梯度,误差反向传播计算梯度的速度大大超过了之前采用的数值微分发法。经过这次改进,我们的神经网络就能以很快的速度和较高的准确率完成MNIST数据集手写数字识别啦!
1.理解误差反向传播
关于误差反向传播的理论和使用计算图推导理解的过程,我之前的文章:Python深度学习入门笔记 2
理解误差反向传播&用python实现自动微分中已经介绍地很详细了啦,如果你对误差反向传播还不了解,就先去看看我这两篇文章吧。
2.代码实现
在我们的两层神将网络类中添加一个方法,如下。
def gradient_BP(self,x,t):
w1, w2 = self.params['w1'], self.params['w2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# 正向传播 forward
a1=np.dot(x,w1)+b1
z1=sigmoid(a1)
a2=np.dot(z1,w2)+b2
y=softmax(a2)
# 反向传播 backward
#一
dy=(y-t)/batch_num
#二
grads['b2']=np.sum(dy,axis=0)
#三
grads['w2']=np.dot(z1.T,dy)
#四
da1=np.dot(dy,w2.T)
#五
dz1=sigmoid_grad(a1) * da1
#六
grads['b1'] = np.sum(dz1, axis=0)
#七
grads['w1'] = np.dot(x.T,dz1)
return grads
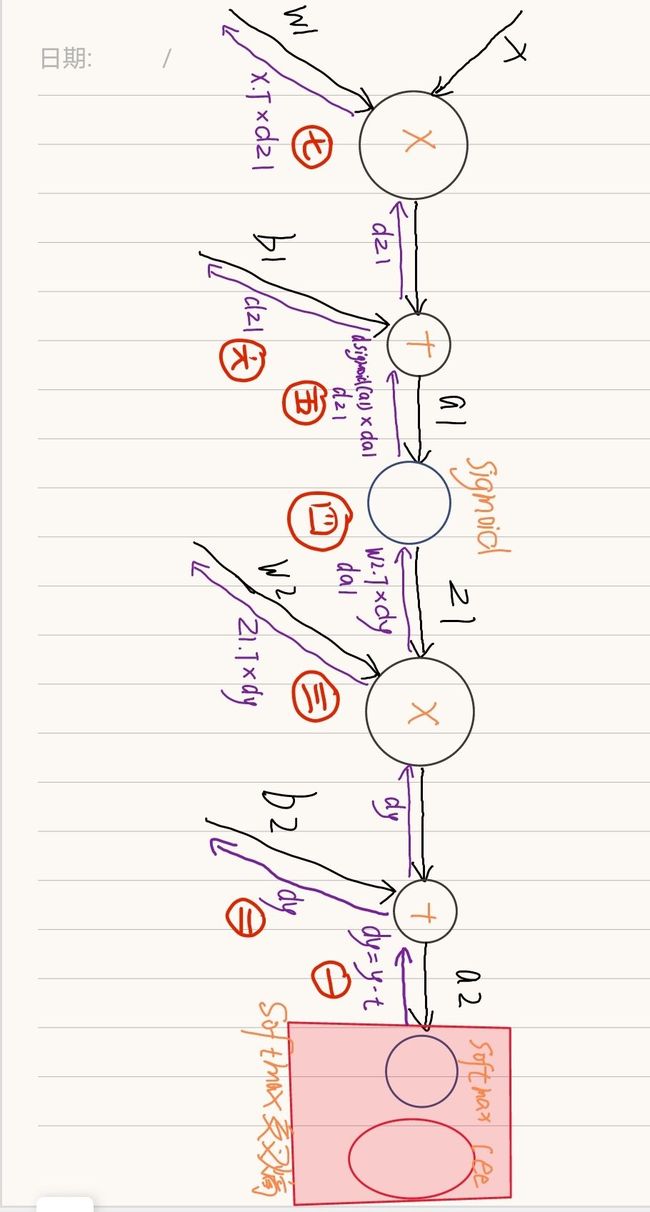
代码中反向传播的每一步都可以在下面的图中找到对应。
需要说明的有两点:
- dy=(y-t)/batch_num 在我之前的文章神经网络中的激活函数与损失函数&深入理解推导softmax交叉熵有详细的解释和推导过程,这里只说一下结论:
如果神经网络输出层使用softmax激活函数,并且使用交叉熵误差,那么反向传播时,经过交叉熵和softmax后流出的值是(y-t)如下图
![]()
之后除以batch_num是得到平均值。
下面是实现的代码:
def sigmoid_grad(x):
return (1.0 - sigmoid(x)) * sigmoid(x)
3.使用神经网络训练MNIST数据集手写数字识别
使用这个神经网络的代码和上篇文章的几乎一样,只有计算梯度的那一行做了替换。
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network=Myself_Two_Layer_Net(input_size=784, hidden_size=100, output_size=10,weight_init_std=0.01)
train_size = x_train.shape[0]
test_size = x_test.shape[0]
learning_rate = 0.1 # 学习率
iters_num = 10000 # 这次终于可以火力全开了
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 计算梯度 这里使用了误差反向传播的高效方法!!!!!!!!!!!!!!!!!
# grad = network.gradient_numerical(x_batch, t_batch)
grad= network.gradient_BP(x_batch,t_batch)
# 更新参数
for key in ('w1', 'b1', 'w2', 'b2'):
key
network.params[key] -= learning_rate * grad[key]
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))
# 绘制图形
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
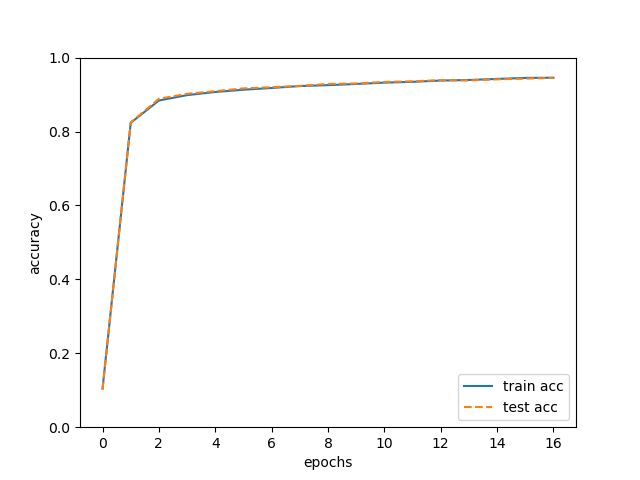
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
同时,我们现在可以把循环次数设置为10000次,然后来训练MNIST数据集手写数字识别
执行代码:
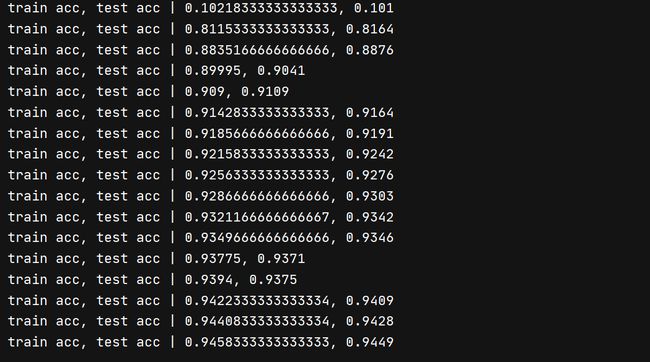
在我的电脑上,只用了不到一分钟就训练完成了(在没有实现误差反向传播的代码,即使把循环次数设置成5,1分钟也跑不完)而且可以看到准确率在94%以上!
46124862724)]
[外链图片转存中…(img-WVB5y6gq-1646124862725)]
在我的电脑上,只用了不到一分钟就训练完成了(在没有实现误差反向传播的代码,即使把循环次数设置成5,1分钟也跑不完)而且可以看到准确率在94%以上!