前言
上周我们数学老师给了我们一道题,大意就是两个向量a和b,一个点M=$x*a+y*b$,x,y有范围,然后所有M组成的面积是一个定值,求x+y的最小值。当然这是道小水题,但我在想,如果把两个向量变成多个向量,二维变成高维的话,那会怎么样呢。
分析
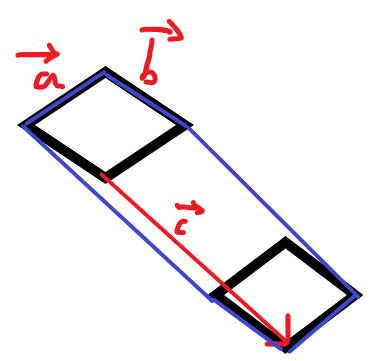
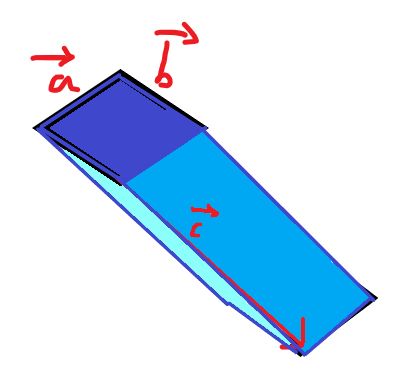
众所周知,两个二维向量可围成平行四边形。如果再多一个就相当于将该平行四边形沿该向量平移,如下图,总面积就相当于如图蓝色框出的面积(即平移时扫过的体积)。
它可以分解成下图三个平行四边形
所以$S=a \times b +a \times c +b \times c$(注意这里为了方便向量不标箭头)
如果再加一个向量,就相当于将该图形整体平移
易得:对于m个二维向量,围成的面积
$$S=\sum_{a,b是1到m的一个组合} a \times b$$
进一步,将二维扩展为三维,对于三个三维向量围成的平行四边形体,此时再加一个向量,就相当于将该几何体平移,求整个几何体扫过的体积。
经过我画图验证可得总体积
$$V=\sum_{a,b,c是1到m的一个组合} (a \times b) \cdot c$$
更进一步,扩展到n维,此时它的体积(我也不知道高维下的空间大小叫什么,就先沿用体积好了)就难以用点积和叉积表示了,我们用$f(a_1,a_2,...,a_n)$表示n个n维向量围成的体积,则:
$$V=\sum_{i,j,k,...是1到m的一个组合} f(a_i,a_j,a_k,...)$$
$f(a_i)$可以用行列式来求解,即:
设m个n维向量分别表示为$v_i=(a_{i,1},...,a_{i,n})$
$f(a_1,a_2,...,a_n)=$
\left[
\begin{array}{cccc}
a_{1,1} & ... & a_{1,n} \\
... & ... & ...\\
a_{n,1} & ... & a_{n,n}
\end{array}
\right]
如此一来,我们就得到了多个n维向量围成的n维体积的大小的计算公式