数据预处理(七)——利用sklearn进行数据预处理

主要内容：
数据预处理的必要性
数据清洗
数据集成
数据标准化
数据规约
数据变换与离散化
利用sklearn进行数据预处理
小结

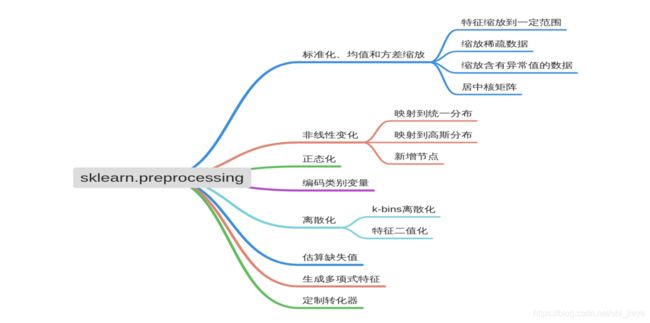
七、利用sklearn进行数据预处理

1.数据标准化、均值和方差缩放

sklearn.preprocessing.scale(X, axis=0, with_mean=True, with_std=True, copy=True)

参数	数据类型	意义
X	（array-like，sparse，matrix）	以此数据为中心缩放
axis	int(0 by default)	轴向设置，置为0表示独立地标准化每个特征，1表示标准化每个样本（即行）
with_mean	boolean,True by default	如果是True，缩放之前先中心化数据
with_std	boolean,True by default	如果是True，以单位方差法缩放数据（或者等价地，单位标准差）
copy	boolean,optional,default,True	False：原地执行行标准化并避免复制

数据的标准化、均值和标准差求解示例。

from sklearn import preprocessing
import numpy as np
X_train = np.array([[1.,-2.,1.5],[2.2,1.3,0.5],[0.3,1.,-1.5]])
X_scaled = preprocessing.scale(X_train)
print('X_train:\n',X_train)
print('X_scaled:\n',X_scaled)
print('均值：',X_scaled.mean(axis=0))
print('单位方差：',X_scaled.std(axis=0))

# X_train:
#  [[ 1.  -2.   1.5]
#  [ 2.2  1.3  0.5]
#  [ 0.3  1.  -1.5]]
# X_scaled:
#  [[-0.21242964 -1.40942772  1.06904497]
#  [ 1.31706379  0.80538727  0.26726124]
#  [-1.10463415  0.60404045 -1.33630621]]
# 均值： [0. 0. 0.]
# 单位方差： [1. 1. 1.]

数据的标准化计算示例。

scaler = preprocessing.StandardScaler().fit(X_train)
print('scaler.scale_:',scaler.scale_)
print('scaler.mean_:',scaler.mean_)
scaler.transform(X_train)

# scaler.scale_: [0.78457349 1.48996644 1.24721913]
# scaler.mean_: [1.16666667 0.1        0.16666667]
# array([[-0.21242964, -1.40942772,  1.06904497],
#        [ 1.31706379,  0.80538727,  0.26726124],
#        [-1.10463415,  0.60404045, -1.33630621]])

X_test = [[-1.,1.,0.]]
scaler.transform(X_test)

# array([[-2.76158538,  0.60404045, -0.13363062]])

2.特征缩放

（1）一般特征值缩放

sklearn.preprocessing.minmax_scale(X, feature_range=(0, 1), axis=0, copy=True)

数据的缩放示例。

X_train = np.array([[ 1., -1.,  2.],[ 2.,  0.,  0.],[ 0.,  1., -1.]])
min_max_scaler = preprocessing.MinMaxScaler()
X_train_minmax = min_max_scaler.fit_transform(X_train)
print('原数据：\n',X_train)
print('归一化：\n',X_train_minmax)

X_test = np.array([[-3., -1.,  4.]])
X_test_minmax = min_max_scaler.transform(X_test)
print('测试数据：',X_test)
print('归一化的测试数据：\n',X_test_minmax)
print('',min_max_scaler.scale_)
print('',min_max_scaler.min_)

# 原数据：
#  [[ 1. -1.  2.]
#  [ 2.  0.  0.]
#  [ 0.  1. -1.]]
# 归一化：
#  [[0.5        0.         1.        ]
#  [1.         0.5        0.33333333]
#  [0.         1.         0.        ]]
# 测试数据： [[-3. -1.  4.]]
# 归一化的测试数据：
#  [[-1.5         0.          1.66666667]]
#  [0.5        0.5        0.33333333]
#  [0.         0.5        0.33333333]

MinMaxScaler默认转换为[0.0,1.0]，如果MinMaxScaler给出一个显式范围feature_range = (min,max),完整的表达式为：

X_std = (X-X.min(axis=0))/(X.max(axis=0)-X.min(axis=0))
X_scaled = X_std*(max-min)+min

MaxAbsScaler的工作方式类似，但通过除以每个特征中的最大值将训练数据置于[-1,1]范围内。它适用于已经零中心化数据或稀疏数据。

利用MaxAbsScaler将数据归一化。

X_train = np.array([[ 1., -1.,  2.],[ 2.,  0.,  0.],[ 0.,  1., -1.]])
max_Abs_scaler = preprocessing.MaxAbsScaler()
X_train_minmax = max_Abs_scaler.fit_transform(X_train)
print('原数据：\n',X_train)
print('归一化：\n',X_train_minmax)

X_test = np.array([[-3., -1.,  4.]])
X_test_maxAbs = max_Abs_scaler.transform(X_test)
print('测试数据：',X_test)
print('归一化的测试数据：',X_test_maxAbs)

# 原数据：
#  [[ 1. -1.  2.]
#  [ 2.  0.  0.]
#  [ 0.  1. -1.]]
# 归一化：
#  [[ 0.5 -1.   1. ]
#  [ 1.   0.   0. ]
#  [ 0.   1.  -0.5]]
# 测试数据： [[-3. -1.  4.]]
# 归一化的测试数据： [[-1.5 -1.   2. ]]

（2）缩放稀疏数据
将稀疏数据居中会破坏数据中的稀疏结构，但是缩放稀疏矩阵又是有意义的，特别是当特征处于不同的缩放比例。

（3）带异常值的缩放数据
如果您的数据包含许多异常值，则使用数据的平均值和方差进行缩放可能不会很好地工作。可以使用：robust_scale和Robust_Scaler替代。

3.非线性变换

非线性变换有分位数转换和幂转换。分位数变换和幂变换都是基于特征的单调变换，从而保持每个特征值的秩。分位数变换将所有特征置于相同的期望分布中。幂变换是一类参数变换，其目的是将数据从任意分布映射到接近高斯分布的位置。

（1）映射到均匀分布
QuantileTransformer()方法和quantile_transform提供非参数转换，将数据映射到值为0~1的均匀分布。

数据映射到值介于0和1之间的均匀分布。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
import numpy as np
X, y = load_iris(return_X_y=True)
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
quantile_transformer = preprocessing.QuantileTransformer(random_state=0)
X_train_trans = quantile_transformer.fit_transform(X_train)
X_test_trans = quantile_transformer.transform(X_test)
print(np.percentile(X_train[:,0],[0,25,50,75,100]))
# 此特征对应于以厘米为单位的萼片长度。
print(np.percentile(X_train_trans[:,0],[0,25,50,75,100]))

# [4.3 5.1 5.8 6.5 7.9]
# [9.99999998e-08 2.38738739e-01 5.09009009e-01 7.43243243e-01
#  9.99999900e-01]

（2）映射到高斯分布

使用Box-Cox将从对数正态分布绘制的样本映射到正态分布的示例。

pt = preprocessing.PowerTransformer(method='box-cox',standardize=False)
X_lognormal = np.random.RandomState(616).lognormal(size=(3,3))
print(X_lognormal)
T = pt.fit_transform(X_lognormal)
print(T)

# [[1.28331718 1.18092228 0.84160269]
#  [0.94293279 1.60960836 0.3879099 ]
#  [1.35235668 0.21715673 1.09977091]]
# [[ 0.49024349  0.17881995 -0.1563781 ]
#  [-0.05102892  0.58863196 -0.57612414]
#  [ 0.69420008 -0.84857822  0.10051454]]

使用QuantileTransformer方法进行数据映射。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
X, y = load_iris(return_X_y=True)
quantile_transformer = preprocessing.QuantileTransformer(output_distribution='normal',random_state=0)
X_trans = quantile_transformer.fit_transform(X)
quantile_transformer.quantiles_

# array([[4.3       , 2.        , 1.        , 0.1       ],
#        [4.31491491, 2.02982983, 1.01491491, 0.1       ],
#        [4.32982983, 2.05965966, 1.02982983, 0.1       ],
#        ...,
#        [7.84034034, 4.34034034, 6.84034034, 2.5       ],
#        [7.87017017, 4.37017017, 6.87017017, 2.5       ],
#        [7.9       , 4.4       , 6.9       , 2.5       ]])

4.正则化

数据正态化示例。

X = [[1.,-1.,2.],[2.,0.,0.],[0.,1.,-1.]]
X_normalized = preprocessing.normalize(X,norm='l2')
X_normalized

# array([[ 0.40824829, -0.40824829,  0.81649658],
#        [ 1.        ,  0.        ,  0.        ],
#        [ 0.        ,  0.70710678, -0.70710678]])

5.编码分类特征
数据编码示例。

enc = preprocessing.OrdinalEncoder()
X = [['male','from US','uses Safari'],['female','from Europe','uses Firefox']]
enc.fit(X)
enc.transform([['female','from US','uses Safari']])

# array([[0., 1., 1.]])

使用OneHotEncoder进行分类特征编码示例。

enc = preprocessing.OneHotEncoder()
X = [['male','from US','uses Safari'],['female','from Europe','uses Firefox']]
enc.fit(X)
R = enc.transform([['female','from US','uses Safari'],['male','from Europe','uses Safari']]).toarray()
display(R)

# array([[1., 0., 0., 1., 0., 1.],
#        [0., 1., 1., 0., 0., 1.]])

类型数据变换示例，数据集中有两种性别，四个可能的大洲和四个网络浏览器。

genders = ['female','male']
locations = ['from Africa','from Asia','from Europe','from US']
browsers = ['uses Chrome','uses Firefox','uses IE','uses Safari']
enc = preprocessing.OneHotEncoder(categories=[genders,locations,browsers])
X = [['male','from US','uses Safari'],['female','from Europe','uses Firefox']]
enc.fit(X)
enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()

# array([[1., 0., 0., 1., 0., 0., 1., 0., 0., 0.]])

6.离散化
（1）K-桶离散化
KBinsDiscretizer将特征离散到K个桶（Bin）中。

数据的K-桶离散化示例。

X = np.array([[-3.,5.,15],[0.,6.,14],[6.,3.,11]])
est = preprocessing.KBinsDiscretizer(n_bins=[3,2,2],encode='ordinal').fit(X)
est.transform(X)

# array([[0., 1., 1.],
#        [1., 1., 1.],
#        [2., 0., 0.]])

（2）特征二值化
特征二值化是对数字特征进行阈值化以获得布尔值的过程。

数据的二值化示例。

X = [[1.,-1.,2.],[2.,0.,0.],[0.,1.,-1.]]
binarizer = preprocessing.Binarizer().fit(X)
Y1 = binarizer.transform(X)
print(Y1)
binarizer = preprocessing.Binarizer(threshold=1.1)
Y2 = binarizer.transform(X)
print(Y2)

# [[1. 0. 1.]
#  [1. 0. 0.]
#  [0. 1. 0.]]
# [[0. 0. 1.]
#  [1. 0. 0.]
#  [0. 0. 0.]]