Parametric ReLU激活函数+注意力机制=自适应参数化ReLU激活函数

本文首先回顾了一些传统的激活函数和注意力机制，然后解读了一种“注意力机制下的新型ReLU激活函数”，也就是自适应参数化修正线性单元（Adaptively Parametric Rectifier Linear Unit，APReLU）。

1.激活函数

激活函数是现代人工神经网络的核心部分，其用处是进行人工神经网络的非线性化。我们首先介绍几种最为常见的激活函数，即Sigmoid、Tanh和ReLU激活函数，分别如图所示。

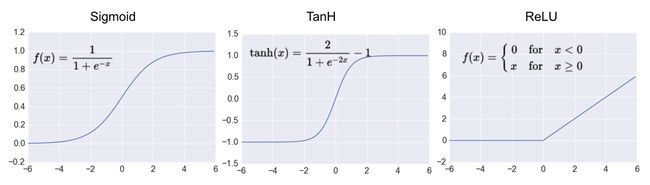
Sigmoid激活函数和Tanh激活函数的梯度取值范围分别是(0,1)和(-1,1)。当层数较多时，人工神经网络可能会遭遇梯度消失的问题。ReLU激活函数的梯度要么是零，要么是一，能够很好地避免梯度消失和梯度爆炸的问题，因此在近年来得到了广泛的应用。

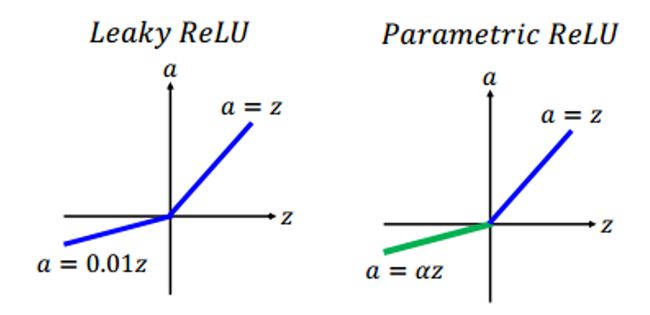
但是，ReLU激活函数依然存在一点问题。倘若在人工神经网络训练的阶段，遇到了特征值全部低于零的情况，那么ReLU激活函数的输出特征就会全部为零。这个时候神经网络就训练失败了。为了回避这种情况，有的学者就提出了leaky ReLU激活函数，不将低于零的特征置为零，而是将低于零的特征乘以一个很小的系数，例如0.1和0.01。

在leaky ReLU激活函数中，这个系数的取值是需要人工设置的。然而人工设置的系数未必是最好的，所以何恺明等人提出了Parametric ReLU激活函数（参数化ReLU激活函数，PReLU激活函数），将这个系数设置为一个可以训练得到的参数，在人工神经网络的训练过程中和其他参数一起采用梯度下降法进行训练。然而，PReLU激活函数有一个特点：一旦训练过程完成，则PReLU激活函数中的这个系数就变成了固定的值。换言之，对于所有的测试样本，PReLU激活函数中这个系数的取值是相同的。

到这里，我们就大概介绍了几种常用的激活函数。这些激活函数有什么问题呢？我们可以思考一下，如果一个人工神经网络采用上述的某种激活函数，抑或是上述多种激活函数的组合，那么这个人工神经网络在训练完成之后，在被应用于测试样本时，对全部测试样本所采用的非线性变换是相同的。也就是说，所有的测试样本，都会经历相同的非线性变换。这其实是一种比较呆板的方式。

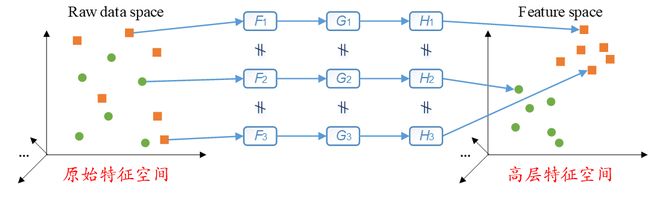
如下图所示，我们如果以左边的散点图表示原始特征空间，以右边的散点图表示人工神经网络所学习得到的高层特征空间，以散点图中的小圆点和小方块代表两种不同类别的样本，以F、G和H表示非线性函数。那么这些样本是通过相同的非线性函数实现原始特征空间到高层特征空间的变换的。也就是说，图片中的“=”意味着，对于这些样本，它们所经历的非线性变换是完全相同的。

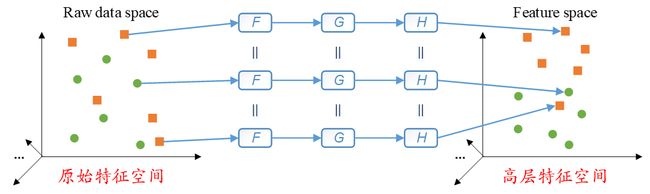
那么，我们能不能根据每个样本的特点，单独为每个样本设置其激活函数的参数、使每个样本经历不同的非线性变换呢？本文后续所要介绍的APReLU激活函数，就做到了这一点。

2.注意力机制

本文所要介绍的APReLU激活函数就借鉴了经典的Squeeze-and-Excitation Network（SENet），而SENet是一种非常经典的、注意力机制下的深度神经网络。SENet的基本原理如下图所示：

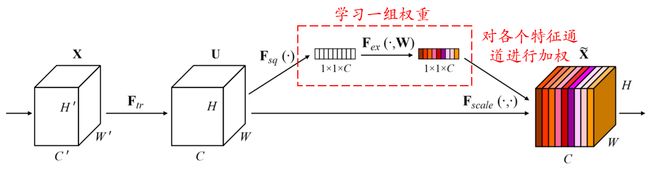
这里简单介绍一下SENet所蕴含的思想。对于许多样本而言，其特征图中的各个特征通道的重要程度很可能是不同的。例如，样本A的特征通道1非常重要，特征通道2不重要；样本B的特征通道1不重要，特征通道2很重要；那么在这个时候，对于样本A，我们就应该把注意力集中在特征通道1（即赋予特征通道1更高的权重）；反之，对于样本B，我们应该把注意力集中在特征通道2（即赋予特征通道2更高的权重）。

为了实现这个目的，SENet通过一个小型的全连接网络，学习得到了一组权重系数，对原先特征图的各个通道进行加权。通过这种方式，每个样本（包括训练样本和测试样本）都有着自己独特的一组权重，用于自身各个特征通道的加权。这其实是一种注意力机制，即注意到重要的特征通道，进而赋予其较高的权重。

3.自适应参数化修正线性单元（APReLU）激活函数

APReLU激活函数，在本质上，就是SENet和PReLU激活函数的集成。在SENet中，小型全连接网络所学习得到的权重，是用于各个特征通道的加权。APReLU激活函数也通过一个小型的全连接网络获得了权重，进而将这组权重作为PReLU激活函数里的系数，即负数部分的权重。APReLU激活函数的基本原理如下图所示。

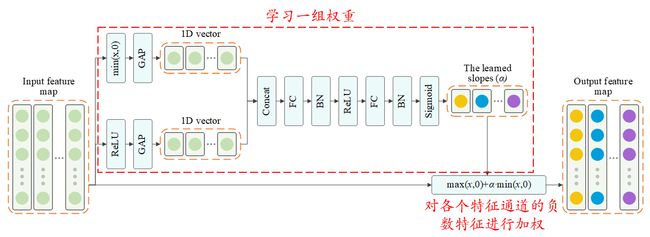
我们可以看到，在APReLU激活函数中，其非线性变换的函数形式是和PReLU激活函数一模一样的。唯一的差别在于，APReLU激活函数里对负数特征的权重系数，是通过一个小型全连接网络学习得到的。当人工神经网络采用APReLU激活函数时，每个样本都可以有自己独特的权重系数，即独特的非线性变换（如下图所示）。同时，APReLU激活函数的输入特征图和输出特征图有着相同的尺寸，这意味着APReLU可以被轻易地嵌入到现有的深度学习算法之中。

综上可知，APReLU激活函数可以使每个样本都有自己独特的一组非线性变换，提供了一种更加灵活的非线性变换方式，具备提高深度学习算法准确率的潜力。

参考文献

M. Zhao, S. Zhong, X. Fu, et al. Deep residual networks with adaptively parametric rectifier linear units for fault diagnosis[J]. IEEE Transactions on Industrial Electronics, 2020, DOI: 10.1109/TIE.2020.2972458.

https://ieeexplore.ieee.org/document/8998530/