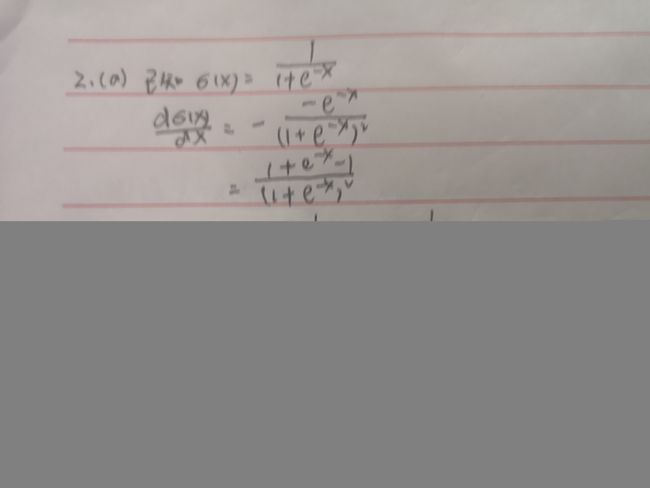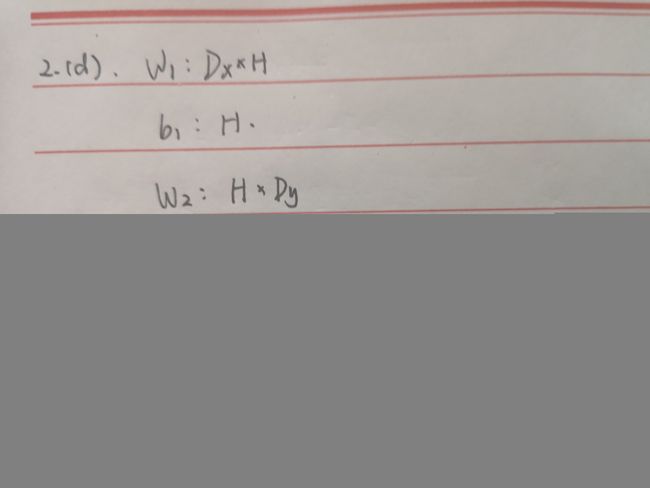CS224N刷题——Assignment1.1&1.2_Softmax&神经网络基础

Assignment #1

1.Softmax

(a)证明softmax对输入中的常量偏移保持不变，即对于任何输入向量x和任何常量c，

式中，x+c意味着将常数c加到x的每个维上。记住：

注：在实践中，我们利用这一性质，在计算数值稳定性的softmax概率时，选择。（即从x的所有元素中减去其最大元素）

(b)给出n行和d列的输入矩阵，使用（a）部分的优化方法计算每行的softmax预测。

def softmax(x):
    """Compute the softmax function for each row of the input x.

    It is crucial that this function is optimized for speed because
    it will be used frequently in later code. You might find numpy
    functions np.exp, np.sum, np.reshape, np.max, and numpy
    broadcasting useful for this task.

    Numpy broadcasting documentation:
    http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html

    You should also make sure that your code works for a single
    D-dimensional vector (treat the vector as a single row) and
    for N x D matrices. This may be useful for testing later. Also,
    make sure that the dimensions of the output match the input.

    You must implement the optimization in problem 1(a) of the
    written assignment!

    Arguments:
    x -- A D dimensional vector or N x D dimensional numpy matrix.

    Return:
    x -- You are allowed to modify x in-place
    """
    orig_shape = x.shape
    
    # YOUR CODE HERE
    if len(x.shape) > 1:
        # Matrix
        x -= np.max(x, axis=1, keepdims=True)  # axis=1按行求最大值
        x = np.exp(x) / np.sum(np.exp(x), axis=1, keepdims=True)
    else:
        # Vector
        x -= np.max(x)
        x = np.exp(x) / np.sum(np.exp(x))
    # END YOUR CODE
    
    assert x.shape == orig_shape
    return x

2.Neural Network Basics

(a)推导出sigmoid函数的梯度，并证明它可以重写为函数值的函数（在表达式中只有σ（x），而不是x）。假设输入x是这个问题的标量。回想一下，sigmoid函数是：

(b)当使用交叉熵损失函数进行评估时，推导softmax函数的梯度，即当预测为时，找出关于输入向量为θ的softmax函数的梯度。记住交叉熵函数为：

其中y是one-hot形式的标签向量，是对所有类别的预测概率向量。

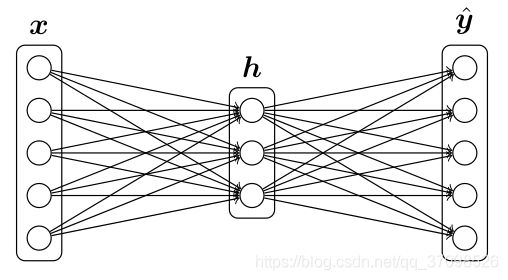
(c)推导关于输入x的单隐层神经网络的梯度（找到，其中是神经网络的损失函数）。该神经网络在隐藏层使用sigmoid激活函数，在输出层使用softmax函数。假设y是one-hot形式的标签向量，且使用交叉熵损失函数。（可使用作为sigmoid函数梯度的简写）

记住，正向传播如下：

(d)在该神经网络中有多少个参数？假设输入为，输出为，隐藏层单元个数为H。

(e)实现sigmoid激活函数及其梯度。

def sigmoid(x):
    """
    Compute the sigmoid function for the input here.

    Arguments:
    x -- A scalar or numpy array.

    Return:
    s -- sigmoid(x)
    """

    # YOUR CODE HERE
    s = 1 / (1 + np.exp(-x))
    # END YOUR CODE
    
    return s


def sigmoid_grad(s):
    """
    Compute the gradient for the sigmoid function here. Note that
    for this implementation, the input s should be the sigmoid
    function value of your original input x.

    Arguments:
    s -- A scalar or numpy array.

    Return:
    ds -- Your computed gradient.
    """
    
    # YOUR CODE HERE
    ds = s * (1 - s)
    # END YOUR CODE
    
    return ds

(f)为了更方便地debug，实现一个梯度检测的程序。

# First implement a gradient checker by filling in the following functions
def gradcheck_naive(f, x):
    """ Gradient check for a function f.

    Arguments:
    f -- a function that takes a single argument and outputs the
         cost and its gradients
    x -- the point (numpy array) to check the gradient at
    """

    rndstate = random.getstate()  # 返回一个当前生成器的内部状态的对象
    random.setstate(rndstate)  # 传入一个先前利用getstate方法获得的状态对象，使得生成器恢复到这个状态。
    fx, grad = f(x) # Evaluate function value at original point
    h = 1e-4        # Do not change this!

    # Iterate over all indexes ix in x to check the gradient.
    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])  # 迭代对象nditer提供了一种灵活访问一个或者多个数组的方式
    while not it.finished:
        ix = it.multi_index

        # Try modifying x[ix] with h defined above to compute numerical
        # gradients (numgrad).

        # Use the centered difference of the gradient.
        # It has smaller asymptotic error than forward / backward difference
        # methods. If you are curious, check out here:
        # https://math.stackexchange.com/questions/2326181/when-to-use-forward-or-central-difference-approximations

        # Make sure you call random.setstate(rndstate)
        # before calling f(x) each time. This will make it possible
        # to test cost functions with built in randomness later.

        # YOUR CODE HERE
        x[ix] += h  # x+h
        random.setstate(rndstate)
        f1 = f(x)[0]  # f(x+h)

        x[ix] -= 2 * h  # f(x-h)
        random.setstate(rndstate)
        f2 = f(x)[0]  # f(x-h)

        numgrad = (f1 - f2) / (2 * h)  # (f(x+h) - f(x-h)) / 2h

        x[ix] += h  # 还原ix
        # END YOUR CODE
        
        # Compare gradients
        reldiff = abs(numgrad - grad[ix]) / max(1, abs(numgrad), abs(grad[ix]))
        if reldiff > 1e-5:
            print("Gradient check failed.")
            print("First gradient error found at index %s" % str(ix))
            print("Your gradient: %f \t Numerical gradient: %f" % (
                grad[ix], numgrad))
            return

        it.iternext() # Step to next dimension

    print("Gradient check passed!")

(g)实现拥有一个sigmoid隐层的神经网络的前向传播和反向传播过程。

推导过程：

代码实现：

def forward_backward_prop(X, labels, params, dimensions):
    """
    Forward and backward propagation for a two-layer sigmoidal network

    Compute the forward propagation and for the cross entropy cost,
    the backward propagation for the gradients for all parameters.

    Notice the gradients computed here are different from the gradients in
    the assignment sheet: they are w.r.t. weights, not inputs.

    Arguments:
    X -- M x Dx matrix, where each row is a training example x.
    labels -- M x Dy matrix, where each row is a one-hot vector.
    params -- Model parameters, these are unpacked for you.
    dimensions -- A tuple of input dimension, number of hidden units
                  and output dimension
    """

    # Unpack network parameters (do not modify)
    ofs = 0
    Dx, H, Dy = (dimensions[0], dimensions[1], dimensions[2])

    W1 = np.reshape(params[ofs:ofs + Dx * H], (Dx, H))
    ofs += Dx * H
    b1 = np.reshape(params[ofs:ofs + H], (1, H))
    ofs += H
    W2 = np.reshape(params[ofs:ofs + H * Dy], (H, Dy))
    ofs += H * Dy
    b2 = np.reshape(params[ofs:ofs + Dy], (1, Dy))

    # YOUR CODE HERE
    # Note: compute cost based on `sum` not `mean`.
    # forward propagation
    m = len(X)
    z1 = np.dot(X, W1) + b1  # (N, H)
    h = sigmoid(z1)  # (N, H)
    z2 = np.dot(h, W2) + b2  # (N, Dy)
    y_hat = softmax(z2)  # (N, Dy)
    cost = np.sum(-labels * np.log(y_hat)) / m

    # backward propagation
    gradz2 = y_hat - labels
    # (N, Dy) 交叉熵的导数dz2为y_hat-y
    gradW2 = np.dot(h.T, gradz2) / m
    # (H, Dy) dW2为J对W2求偏导,dW2=h.T*dz2/N,其中h.T(H, N),dz2(N, Dy)
    gradb2 = np.sum(gradz2, axis=0, keepdims=True) / m
    # (1, Dy) db2为J对b2求偏导,db2=y_hat-y(N, Dy)在列方向上求和
    gradz1 = np.dot(gradz2, W2.T) * sigmoid_grad(h)
    # (N, H) dz1为J对z1求偏导,dz1=dz2*W2.T*sigmoid_grad(z1),其中dz2(N, Dy),W2.T(Dy, H),sigmoid`(z1)(N, H),哈达玛积
    gradW1 = np.dot(X.T, gradz1) / m
    # (Dx, H) dW1为J对W1求偏导,dW1=X.T*dz1,其中X.T(Dx, N),dz1(N, H)
    gradb1 = np.sum(gradz1, axis=0, keepdims=True) / m
    # (1, H) db1为J对b1求偏导,db1=dz1(N, H)在列方向上求和
    # END YOUR CODE
    
    # Stack gradients (do not modify)
    grad = np.concatenate((gradW1.flatten(), gradb1.flatten(), gradW2.flatten(), gradb2.flatten()))

    return cost, grad