双目立体视觉学习笔记(一)
双目立体视觉
立体视觉(Stereo Vision)又称为三维视觉,它通过两个或多个相机采集被测目标的图像,并将这些图像调整至同一平面,然后基于其中同一被测特征点所对应像素间的差异来重建三维信息或实现三维测量。研究立体视觉技术,可以将机器视觉系统的应用范围从二维平面扩展到三维环境。
立体视觉被广泛用于三维导航、三维定位、目标追踪和机器人研究等工业领域。例如,双目机器人可以使用三维信息来测量障碍物的尺寸和距离,以进行准确的路径规划。在目标分拣应用中,使用立体视觉系统可以避免部件被遮挡和照明变化对定位的影响,为机器手臂提供精确的目标位置信息。这就使得立体视觉特别适合那些需要机械手从包装箱或其他容器中分拣出某一特定 3D 对象的应用。立体视觉系统对于亮度变化和阴影可保持不变性,因此可还可用于目标追踪、自动驾驶系统障碍物检测等场合。
基于双相机构建的双目视觉(Binocular Stereo Vision)系统是最小的立体视觉系统。它能完成大多数三维场景下的任务,而且多目视觉系统可看作是多个双目系统的组合,因此对双目系统的研究就成了立体视觉系统的研究重点。本章着重介绍双目立体视觉系统的原理、系统校准、图像调整、图像关联以及场景深度信息计算等技术。
1.双目视觉系统原理
双目视觉系统与生物的眼睛类似,不仅可以获取场景的平面图像信息,还能计算被测目标的距离和相对深度信息。图 1显示了双目视觉的示意图,由图可见,世界坐标系中被测目标表面上任一点 P ( X W , Y W , Z W ) P(X_{W},Y_{W},Z_{W} ) P(XW,YW,ZW),在左相机坐标系中像面上的投影点为 p ( u L , v L ) p(u_{L},v_{L}) p(uL,vL),在右相机坐标系中像面上的投影点为 p ( u R , v R ) p(u_{R},v_{R}) p(uR,vR)。若仅用有一个相机的单目视觉系统观察,只能获知点 P ( X W , Y W , Z W ) P(X_{W},Y_{W},Z_{W} ) P(XW,YW,ZW),可能位于左相机光心 O L O_{L} OL与点 p ( u L , v L ) p(u_{L},v_{L}) p(uL,vL)所构成的射线上,或位于右相机光心 O R O_{R} OR与点 p ( u R , v R ) p(u_{R},v_{R}) p(uR,vR)所构成的射线上。但是若同时用有两个相机的双目视觉系统观察,并且如果能确定像点 ( u L , v L ) (u_{L},v_{L}) (uL,vL)和 ( u R , v R ) (u_{R},v_{R}) (uR,vR)对应于同一空间特征点 P ( X W , Y W , Z W ) P(X_{W},Y_{W},Z_{W} ) P(XW,YW,ZW),就可以通过两个像点与相机光心所构成的两直线的交点计算出点 P ( X W , Y W , Z W ) P(X_{W},Y_{W},Z_{W} ) P(XW,YW,ZW)的确切位置。注意,由于相机成倒立图像,图1中将正立相面置于相机前方焦距处,以方便讨论。

图 1 双目视觉示意图
根据相机小孔成像原理,其成像过程可用几何投影法来表示,如图2所示。其中 O c O_{c} Oc点为相机光心, O c Z c O_{c}Z_{c} OcZc为相机光轴, O c − X c Y c Z c O_{c}-X_{c}Y_{c}Z_{c} Oc−XcYcZc组成的直角坐标系为相机坐标系。 O I O_{I} OI位于相机光轴与图像平面(焦距处)的交点,它一般位于图像中心。 O I − u v O_{I}-uv OI−uv组成的直角坐标系为图像坐标系。若将相机抽象为小孔成像模型,则相机坐标系中任意一空间点 P ( X c , Y c , Z c ) P(X_{c},Y_{c},Z_{c}) P(Xc,Yc,Zc)在图像平面中的位置 p u , v p_{u,v} pu,v,为光心和点 P ( X c , Y c , Z c ) P({X_{c},Y_{c},Z_{c})} P(Xc,Yc,Zc)的连线与图像平面的角点。这种关系称为中心透视投影(Perspective Projection)。

图 2 三维空间与相面的投影关系
根据三角比例关系,若已知点 P P P在相机坐标系 O c − X c Y c Z c O_{c}-X_{c}Y_{c}Z_{c} Oc−XcYcZc中的坐标 P ( X c , Y c , Z c ) P({X_{c},Y_{c},Z_{c})} P(Xc,Yc,Zc),则可得到图像坐标系 O I − u v O_{I}-uv OI−uv中像点坐标 p ( u , v ) p(u,v) p(u,v)与它的关系:
{ u = f ∗ X c Z c v = f ∗ Y c Z c \begin{cases} u=f*\frac{X_{c}}{Z_{c}} \\ v=f*\frac{Y_{c}}{Z_{c}} \end{cases} {u=f∗ZcXcv=f∗ZcYc
可得
{ X c = u ∗ Z c f Y c = v ∗ Z c f \begin{cases} X_{c}=\frac{u * Z_{c}}{f} \\ Y_{c}=\frac{v * Z_{c}}{f} \end{cases} {Xc=fu∗ZcYc=fv∗Zc
其中, f f f为相机像平面与相机坐标系原点之间的距离(一般为相机的焦距)。坐标 Z c Z_{c} Zc为物距,它决定相机图像的大小,其值越大,相机所成图像越小。若用齐次坐标和矩阵来表示上述关系,则上式可写为
Z c [ u v 1 ] = [ f 0 0 0 0 f 0 0 0 0 1 0 ] [ X c Y c Z c 1 ] Z_{c}\begin{bmatrix}u \\v \\1 \end{bmatrix}=\begin{bmatrix}f & 0 & 0 & 0\\0 &f & 0 & 0\\0 & 0 & 1&0 \end{bmatrix}\begin{bmatrix}X_{c} \\Y_{c} \\Z_{c} \\1 \end{bmatrix} Zc⎣⎡uv1⎦⎤=⎣⎡f000f0001000⎦⎤⎣⎢⎢⎡XcYcZc1⎦⎥⎥⎤
齐次坐标是一种 n + 1 n+1 n+1维向量表示一个 n n n维向量的表示法,它更便于 通过矩阵相乘的形式来表示低维空间中用矩阵乘法和加法表示的仿射变换(Affine Transformation),即坐标的平移、缩放、旋转、倾斜或者它们的组合,如图3所示。

图3 齐次坐标与仿射变换
继续相机投影关系的讨论,若已知相机传感器上物理像素的尺寸 ( d x , d y ) (d_{x},d_{y}) (dx,dy)和 O I O_{I} OI相对图像左上角的距离 ( u 0 , v 0 ) (u_{0},v_{0}) (u0,v0),则可得到以像素为单位的像点的坐标 p ( i , j ) p(i,j) p(i,j):
{ i = u d x + u 0 = f ⋅ X c Z c ⋅ d x + u 0 j = v d y + v 0 = f ⋅ Y c Z c ⋅ d y + v 0 ⇒ Z c [ i j 1 ] = [ 1 d x 0 u 0 0 1 d y v 0 0 0 1 ] ⋅ [ f 0 0 0 0 f 0 0 0 0 1 0 ] [ X c Y c Z c 1 ] \left\{\begin{matrix}i = \frac{u}{d_{x}}+u_{0}=\frac{f\cdot X_{c} }{Z_{c} \cdot d_{x}}+u_{0} \\ \\j = \frac{v}{d_{y}}+v_{0}=\frac{f\cdot Y_{c} }{Z_{c} \cdot d_{y}}+v_{0} \end{matrix} \right. \Rightarrow Z_{c}\begin{bmatrix}i \\j \\1 \end{bmatrix} =\begin{bmatrix}\frac{1}{d_{x}} &0 &u_{0} \\0 &\frac{1}{d_{y}} &v_{0} \\0 &0 &1 \end{bmatrix} \cdot \begin{bmatrix}f &0 &0 &0\\0 &f &0 &0\\0 &0 &1 &0 \end{bmatrix} \begin{bmatrix}X_{c} \\Y_{c} \\Z_{c} \\1 \end{bmatrix} ⎩⎪⎨⎪⎧i=dxu+u0=Zc⋅dxf⋅Xc+u0j=dyv+v0=Zc⋅dyf⋅Yc+v0⇒Zc⎣⎡ij1⎦⎤=⎣⎡dx1000dy10u0v01⎦⎤⋅⎣⎡f000f0001000⎦⎤⎣⎢⎢⎡XcYcZc1⎦⎥⎥⎤
也就是说,若已知空间某点在相机坐标系中的坐标 P ( X c , Y c , Z c ) P(X_{c},Y_{c},Z_{c}) P(Xc,Yc,Zc),就能根据投影关系和相机的内部参数(焦距 f f f、物理像素大小等),计算得到像点在图像坐标系中的位置。
但是实际开发时,空间点的位置并不一定都用相机的坐标来表示,而是可能在环境中选择一个基准坐标系来描述相机和环境中的物体的位置,该坐标系称为世界坐标系。空间点在相机坐标系与世界坐标系中的坐标可以通过旋转与平移来转换,表示为:
P c = R P w + B ⇔ [ X c Y c Z c 1 ] = [ R B 0 1 ] [ X W Y W Z W 1 ] \mathbf{P}_{c}=\mathbf{RP_\mathrm{w}}+\mathbf{B}\Leftrightarrow \begin{bmatrix}X_{c} \\Y_{c} \\Z_{c} \\1 \end{bmatrix} =\begin{bmatrix}\mathbf{R} &\mathbf{B} \\ \mathbf{0} &1\end{bmatrix}\begin{bmatrix}X_{W} \\Y_{W} \\Z_{W} \\1 \end{bmatrix} Pc=RPw+B⇔⎣⎢⎢⎡XcYcZc1⎦⎥⎥⎤=[R0B1]⎣⎢⎢⎡XWYWZW1⎦⎥⎥⎤
其中 P W = ( X W , Y W , Z W ) T \mathbf{P_\mathrm{W}}=(X_{W},Y_{W},Z_{W})^{T} PW=(XW,YW,ZW)T为空间点的世界坐标, P c = ( X c , Y c , Z c ) T \mathbf{P_\mathrm{c}}=(X_{c},Y_{c},Z_{c})^{T} Pc=(Xc,Yc,Zc)T为其在相机坐标系中坐标, B = ( b x , b y , b z ) T \mathbf{B}=(b_{x},b_{y},b_{z})^{T} B=(bx,by,bz)T为三维平移向量,表示两坐标系在3个方向上的距离, 0 = ( 0 , 0 , 0 ) \mathbf{0}=(0,0,0) 0=(0,0,0)。 R \mathbf{R} R为3X3的旋转矩阵,它可以分解为3个矩阵的乘积。分解得到3个矩阵分别表示空间点绕X轴(滚转)、绕Y轴(俯仰)、绕Z轴(偏航)的旋转矩阵,如图4所示。

图4 三维坐标转换
综上所述,可以得到以三维空间点世界坐标 P W = ( X W , Y W , Z W ) \mathbf{P_\mathrm{W}}=(X_{W},Y_{W},Z_{W}) PW=(XW,YW,ZW),与其在图像中以像素为单位的坐标 p ( i , j ) p(i,j) p(i,j)之间的如下关系(先将 P w \mathbf{P_\mathrm{w}} Pw转换为相机坐标系坐标,再进行投影变换):

其中, P w ′ = ( X w , Y w , Z w ) T \mathbf{P_\mathrm{w}^{'}}=(X_{w},Y_{w},Z_{w})^{T} Pw′=(Xw,Yw,Zw)T,M 为 3×4 的投影矩阵,由式中各矩阵组合而成。相机的像素大小 ( d x , d y ) (d_{x},d_{y}) (dx,dy),焦距及图像坐标原点到图像左上角的距离 ( u 0 , v 0 ) (u_{0},v_{0}) (u0,v0)均为相机的内部参数,而相机坐标系与世界坐标系之间的旋转和平移矩阵由相机的安装位置和方式决定,属于外部参数。当选定相机并确定了其安装位置和安装方式后,相机的内外参数就能被确定。而此时若已知空间中某点在世界坐标系(预先确定)中的坐标 P w = ( X w , Y w , Z w ) T \mathbf{P_\mathrm{w}}=(X_{w},Y_{w},Z_{w})^{T} Pw=(Xw,Yw,Zw)T,就能得到 3个方程式,在这 3 个方程中消去 Z Z Z.就可求出 p ( i , j ) p(i,j) p(i,j)。但是,若反过来已知空间某点对应的图像点像素坐标 p ( i , j ) p(i,j) p(i,j)和相机的内外参数,从得到的 3 个方程中消去 Z Z Z,却并不能得到该点在世界坐标系中的位置 P w = ( X w , Y w , Z w ) T \mathbf{P_\mathrm{w}}=(X_{w},Y_{w},Z_{w})^{T} Pw=(Xw,Yw,Zw)T,而只能得到关于 X w , Y w X_{w},Y_{w} Xw,Yw和 Z w Z_{w} Zw的两个线性方程。
由这两个线性方程组成的方程组即为图 2 中射线 O c P O_{c}P OcP 的方程,也就是说任何位于该射线上的空间点在图像上的投影点均为 p ( i , j ) p(i,j) p(i,j)。由此可见,仅用单目视觉系统无法确定空间点的确切位置。
双目视觉系统可基于两个相机所采集的图像中两个同源点(Homologous Points)之间的距离,由三角几何法重建空间三维信息。同源点是空间某点在不同图像中的成像点,又称为共轭点(Conjugate Points)。它们在图像中的距离差异称为视差(Disparity)。
研究双目系统时一般先要明确研究过程所涉及的以下几种类型的坐标系(参见图 5):
 图 5 双目系统中的坐标系
图 5 双目系统中的坐标系
(1)世界坐标系。预先在环境中选择的基准三维坐标系,用来描述相机和环境中物体的坐标位置。在双目视觉系统中,一般将左相机坐标系定义为世界坐标系。
(2)相机坐标系。以相机光心为原点,光轴为Z 轴的三维坐标系。在双目系统中,左右两个相机坐标系可通过旋转和平移进行转换。
(3)图像坐标系。相机所成图像的二维坐标系,可以用像素数量描述,也可以用物理尺寸描述。对于相机坐标系中的某个三维空间点,可通过三角投影变换计算得到其再图像坐标系中像点的位置。
根据前述讨论,若定义左相机坐标系就是世界坐标系,那么世界坐标系中的点 P w = ( X w , Y w , Z w ) \mathbf{P_\mathrm{w}}=(X_{w},Y_{w},Z_{w}) Pw=(Xw,Yw,Zw)到左相机的图像坐标系中的位置可直接通过三角投影关系计算得到:
Z w [ u L v L 1 ] = [ f L 0 0 0 0 f L 0 0 0 0 1 0 ] [ X w Y w Z w 1 ] Z_{w}\begin{bmatrix}u_{L} \\v_{L} \\1 \end{bmatrix}=\begin{bmatrix}f_{L} &0 &0 &0 \\0 &f_{L} &0 &0 \\0 &0 &1 &0 \end{bmatrix}\begin{bmatrix}X_{w} \\Y_{w} \\Z_{w} \\1 \end{bmatrix} Zw⎣⎡uLvL1⎦⎤=⎣⎡fL000fL0001000⎦⎤⎣⎢⎢⎡XwYwZw1⎦⎥⎥⎤
其中下标 L表示与左相机相关的值。该点在右侧相机图像坐标系中的位置同样可以通过投影变换计算得到。但是由于投影变换必须在对应的相机坐标系中进行,因此必须先将空间点的世界坐标 P w = ( X w , Y w , Z w ) \mathbf{P_\mathrm{w}}=(X_{w},Y_{w},Z_{w}) Pw=(Xw,Yw,Zw)通过旋转平移变换为右相机坐标系中的坐标 P R = ( X R , Y R , Z R ) \mathbf{P_\mathrm{R}}=(X_{R},Y_{R},Z_{R}) PR=(XR,YR,ZR),然后才能正确计算。表示如下: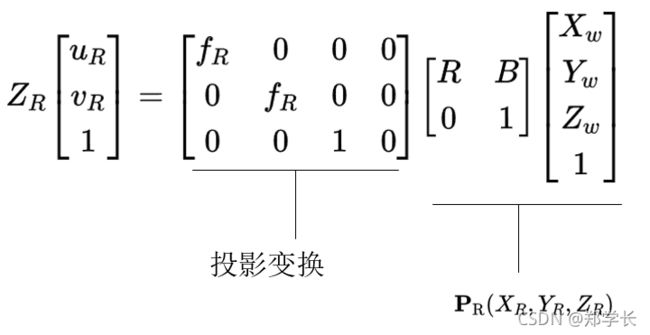
因此,若已知左右相机的坐标系和焦距以及空间中某一点在两个相机图像坐标中的位置,就能通过两个相机的投影变换关系得到 4 个方程。而根据这4个方程,就不难求出空间点的世界坐标 P w = ( X w , Y w , Z w ) \mathbf{P_\mathrm{w}}=(X_{w},Y_{w},Z_{w}) Pw=(Xw,Yw,Zw)。不仅如此,实际开发中常会使用更简单的平视双目系统模型来简化问题。图 6 显示了平视双目系统的结构及其特点。通常来说系统中的两个相机类型相同(至少焦距相同)且平行安装。定义左相机坐标系为世界坐标系,且左右相机坐标系的X 轴共线,并与基线平行。平视双目系统也可以通过移动单个相机来实现,这种情况下,相机的运动轨道必须为直线。
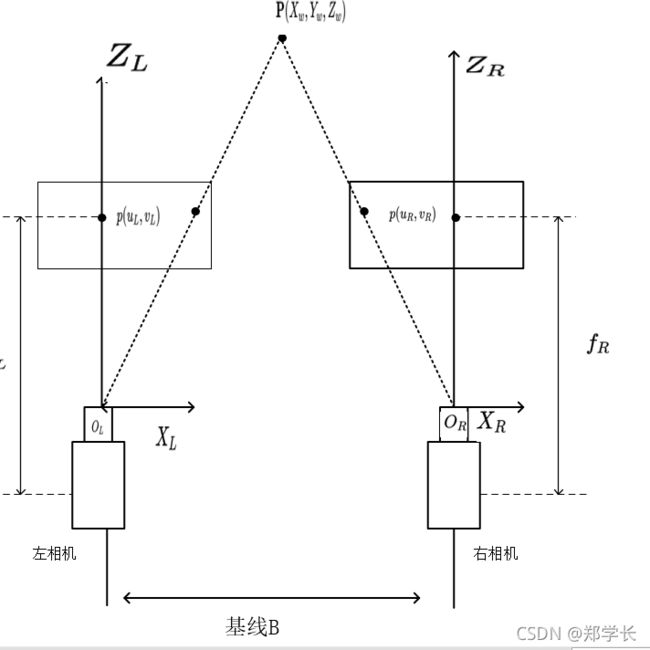
图 6 平视双目系统及其特点
平时双目视觉系统特点:
(1)两个相机类型相同,或者至少焦距相同。
(2)两个相机平行安装,若为单个相机运动系统,则运动轨迹为直线。
(3)两个相机X轴共线,且与基线平行。
(4)定义左相机坐标系为世界坐标系
假定图 6 中平行安装的两个相机中心连线的距离为 B(称为基线),空间点 P w = ( X w , Y w , Z w ) \mathbf{P_\mathrm{w}}=(X_{w},Y_{w},Z_{w}) Pw=(Xw,Yw,Zw)在左右两个相机所成图像的坐标系中的位置分别为 p ( u L , v L ) p(u_{L},v_{L}) p(uL,vL)和 p ( u R , v R ) p(u_{R},v_{R}) p(uR,vR)。由于两个相机类型相同,因此所称图像在同一平面上,从而空间点在两个图像坐标系中Y方向的坐标相同,即 v L = v R v_{L}=v_{R} vL=vR。进一步根据几何关系可得到:
{ u l = f ⋅ X W Y W u R = f ⋅ X W − B Z W v L = v R = f ⋅ Y W Z W \begin{cases}u_{l}=f\cdot \frac{X_{W}}{Y_{W}} \\ \\u_{R}=f\cdot \frac{X_{W}-B}{Z_{W}} \\ \\v_{L}=v_{R}=f\cdot \frac{Y_{W}}{Z_{W}} \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧ul=f⋅YWXWuR=f⋅ZWXW−BvL=vR=f⋅ZWYW
其中 f f f为相机焦距(左右相机焦距相同)。注意,在计算像点在右相机所成图像上的位置时,先通过坐标平移将 P w = ( X w , Y w , Z w ) \mathbf{P_\mathrm{w}}=(X_{w},Y_{w},Z_{w}) Pw=(Xw,Yw,Zw)点的变换到右相机坐标系中,才进行计算。若定义视差 d d d为 p ( u L , v L ) p(u_{L},v_{L}) p(uL,vL)和 p ( u R , v R ) p(u_{R},v_{R}) p(uR,vR)两点在图像中的距离差异,则有:
d = u L − u R = f ⋅ B Z w d=u_{L}-u_{R}=f\cdot \frac{B}{Z_{w}} d=uL−uR=f⋅ZwB
从而有:
Z w = f ⋅ B d = f ⋅ B u L − u R Z_{w}=f\cdot\frac{B}{d}=f\cdot \frac{B}{u_{L}-u_{R}} Zw=f⋅dB=f⋅uL−uRB
因此,只要左相机像面上的任意一点能在右相机像面上找到同源的匹配点,就可以根据视差确定该点的三维坐标。更进一步,只要被测目标像面上的所有点都可在另一相机中找到同源点,就可以确定被测目标的三维坐标。