图像处理——矩

本文转自：https://www.cnblogs.com/ronny/p/3985810.html

本文转自：http://blog.csdn.net/gdfsg/article/details/51015066

1. 矩的概念

2. Hu矩

3. 利用OPENCV计算Hu矩

opencv里对Hu矩的计算有直接的API，它分为了两个函数：moments()函数用于计算中心矩，HuMoments函数用于由中心矩计算Hu矩。

Moments moments(InputArray array, bool binaryImage=false )

参数说明

• 输入参数：array是一幅单通道，8-bits的图像，或一个二维浮点数组(Point of Point2f)。binaryImage用来指示输出图像是否为一幅二值图像，如果是二值图像，则图像中所有非0像素看作为1进行计算。
• 输出参数：moments是一个类：

class Moments
{
public:
    Moments();
    Moments(double m00, double m10, double m01, double m20, double m11,
            double m02, double m30, double m21, double m12, double m03 );
    Moments( const CvMoments& moments );
    operator CvMoments() const;
}

里面保存了图像的2阶与3阶中心矩的值。

void HuMoments(const Moments& moments, double* hu)

参数说明：

• 输入参数：moments即为上面一个函数计算得到的moments类型。
• 输出参数：hu是一个含有7个数的数组。

int main(int argc, char** argv) 
{ 
    Mat image = imread(argv[1]);  
    cvtColor(image, image, CV_BGR2GRAY); 
    Moments mts = moments(image); 
    double hu[7]; 
    HuMoments(mts, hu); 
    for (int i=0; i<7; i++) 
    { 
        cout << log(abs(hu[i])) <<endl; 
    } 
   return 0; 
}

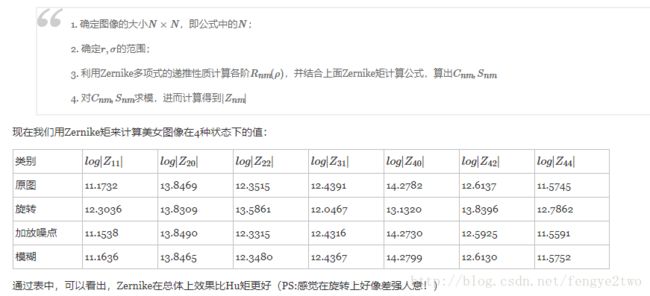
4. Zernike矩

Hu矩在图像描述上有广泛的应用，但是其低阶几何矩与图像整体特征有关，不包含太多的图像细节信息，而高阶几何矩易受噪声影响，因此很难利用几何矩恢复图像。

Zernike矩能够很容易地构造图像的任意高阶矩，并能够使用较少的矩来重建图像。Zernike矩是基于Zernike多项式的正交化函数，虽然其计算比较复杂，但是Zernide矩在图像旋转和低噪声敏感度方面具有较大的优越性。由于Zernike矩具有图像旋转不变性，而且可以构造任意高阶矩，所以被广泛应用对目标进行识别中。

4.1 Zernike矩多项式

4.2 Zernike矩的定义

4.3 Zernike矩的计算

5. 总结

不变矩的应用过程一般包括：

1. 选择合适的不变矩类型；
2. 选择分类器（如神经网络、最短距离等）；
3. 如果是神经网络分类器，则需要计算学习样例的不变矩去训练神经网络；
4. 计算待识别对象的不变矩，输入神经网络就可得到待识别对象的类型，或者计算待识别对象不变矩与类别对象不变矩之间的距离，选择最短距离的类别作为待识别对象的类别。

可以看出，不变矩作用主要目的是描述事物（图像）的特征。人眼识别图像的特征往往又表现为“求和”的形式，因此不变矩是对图像元素进行了积分操作。

不变矩能够描述图像整体特征就是因为它具有平移不变形、比例不变性和旋转不变性等性质。

然而，另一方面图像的各阶不变矩究竟代表的什么特征很难进行直观的物理解释。

1. 数学中的矩

2. 图像的几何矩

     补充一点，懂的请无视：

      可能有人会问，为什么像素点的值表示的是概率？meanshift算法里用到的反向投影图就是概率图。什么又是反向投影图呢？举个例子。

    （1）例如灰度图像如下

      Image=

      0 1 2 3

      4 5 6 7

      8 9 10 11

      8 9 14 15

    （2）该灰度图的直方图为（bin指定的区间为[0,4)，[4,7)，[7,12)，[12,16)）

      Histogram=

      4 3 7 2

    （3）反向投影图

      Back_Projection=

      4 4 4 4

      3 3 3 7

      7 7 7 7

      7 7 2 2

      可见，反向投影图就是反应了颜色分布的概率图。

3. 几个图像的不变矩

HU矩

       这7个不变矩构成一组特征量，Hu.M.K在1962年证明了他们具有旋转，缩放和平移不变性。实际上，在对图片中物体的识别过程中，只有M1和M2不变性保持的比较好，其他的几个不变矩带来的误差比较大，有学者认为只有基于二阶矩的不变矩对二维物体的描述才是真正的具有旋转、缩放和平移不变性(M1和M2刚好都是由二阶矩组成的）。

       由Hu矩组成的特征量对图片进行识别，优点就是速度很快，缺点是识别率比较低。Hu不变矩一般用来识别图像中大的物体，对于物体的形状描述得比较好，图像的纹理特征不能太复杂，像识别水果的形状，或者对于车牌中的简单字符的识别效果会相对好一些。

 

  其他常见的图像矩

        连续正交矩：Zernike矩和Legendre矩

       离散正交矩：Tchebichef矩、Krawtchouk矩、Hahn矩、Racah矩等。

       虽然非正交矩形式简单 、计算快、易于实现,但抗噪性差、基函数非正交 ,且具有较大的信息冗余。连续正交矩的基函数正交,不仅其矩变换可逆 ,且易于图像重建 , 由于其各阶矩相互独立,故具有最小的信息冗余。其不足之处是该矩的基函数只在特定范围内是正交的。

 

4. OpenCV先关函数

      由OPENCV提供计算中心距、归一化中心距和hu矩的函数为：

void cvMoments(const CvArr*image,CvMoments*moments,int isBinary=0)

double cvGetCentralMoment(CvMoments*moments,intx_order,int y_order)

doublecvGetNormalizedCentralMoment(CvMoments*moments,int x_order,int y_order);

voidcvGetHuMoments(CvMoments*moments,CvHuMoments*HuMoments);

     其中cvMoments和上面的cvContourMoments是同一个函数。

     同时OPENCV还提供了输入图像直接进行hu矩匹配的函数是

double cvMatchShapes(constvoid*object1,const void*object2,int method,double parameter=0);

 

5. 小结

        图像的矩通常描述了该图像形状的全局特征，并被广泛的应用在各种图像处理、计算机视觉和机器人技术领域的目标识别与方位估计中。一阶矩与形状有关，二阶矩显示曲线围绕直线平均值的扩展程度，三阶矩则是关于平均值的对称性的测量。不变矩是图像的统计特性，满足平移、伸缩、旋转均不变的不变性。

        如果把图像看成是一块质量密度不均匀的薄板，其图像的灰度分布函数f(x,y)就是薄板的密度分布函数，则其各阶矩有着不同的含义，如零阶矩表示它的总质量；一阶矩表示它的质心；二阶矩又叫惯性矩，表示图像的大小和方向。事实上，如果仅考虑阶次为2的矩集，则原始图像等同于一个具有确定的大小、方向和离心率，以图像质心为中心且具有恒定辐射率的椭圆。

        由三阶矩以下矩构成的七个矩不变量具有平移、旋转和尺度不变性等等。当密度分布函数发生改变时，图像的实质没有改变，仍然可以看做一个薄板，只是密度分布有所改变。虽然此时各阶矩的值可能发生变化，但由各阶矩计算出的不变矩仍具有平移、旋转和尺度不变性。通过这个思想，可对图像进行简化处理，保留最能反映目标特性的信息，再用简化后的图像计算不变矩特征，可减少计算量。

        研究表明，只有基于二阶矩的不变矩对二维物体的描述才是真正的与旋转、平移和尺度无关的。较高阶的矩对于成像过程中的误差，微小的变形等因素非常敏感，所以相应的不变矩基本上不能用于有效的物体识别。即使是基于二阶矩的不变矩也只能用来识别外形相差特别大的物理，否则他们的不变矩会因为很相似而不能识别。