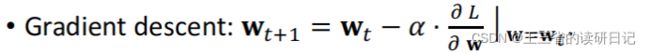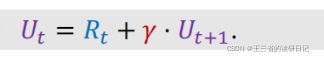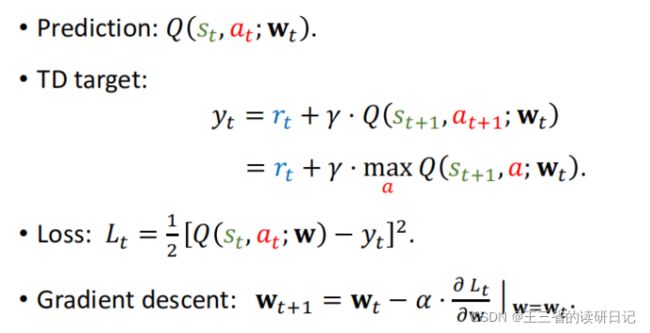强化学习基础07——deep Q-network(DQN)
目录
1. DQN
关于Q*函数请参考强化学习基础概念03——价值函数_王三省的读研日记的博客-CSDN博客中的问题4(optimal action value function最优动作价值函数Q*)
如何理解
具体的算法:
2. TD算法
举个例子:
TD target
如何用TD算法用来学习dqn?
3. 总结:
1. DQN
 DQN全称deep Q-network,是一种价值学习的方法,用一个神经网络去近似Q*函数,我们把神经网络记为Q(s,a;w),神经网络的参数是W,神经网络的输入是状态S,神经网络的输出是很多数值,这些数值是对所有可能的动作的打分,每一个动作对应一个分数,我们通过奖励来学习神经网络,神经网络给动作的打分就会逐渐改进,打分会越来越准。
DQN全称deep Q-network,是一种价值学习的方法,用一个神经网络去近似Q*函数,我们把神经网络记为Q(s,a;w),神经网络的参数是W,神经网络的输入是状态S,神经网络的输出是很多数值,这些数值是对所有可能的动作的打分,每一个动作对应一个分数,我们通过奖励来学习神经网络,神经网络给动作的打分就会逐渐改进,打分会越来越准。
其实就是用个神经网络近似Q*函数,游戏中的agent的目标是打赢游戏。
关于Q*函数请参考强化学习基础概念03——价值函数_王三省的读研日记的博客-CSDN博客中的问题4(optimal action value function最优动作价值函数Q*)
如果用强化学习的语言来说,目标就是在游戏结束的时候,获得的奖励总和越大越好。
既然目标已经定下来了,agent就要努力实现目标。
假设Q*函数是知道的,那么agent该怎么做决策呢?什么才是最优的动作呢?
Q*函数可以给所有的动作打分,每个动作a都有个分数,最好的动作a就是分数最高的动作。
Q*函数就像是个先知一样,它能预见未来的结果。
比如你问先知现在有ABC三个股票,我该把我的钱用来买哪个股票呢?未来是充满随机性的,什么都可能发生。所以先知没有办法给你一个确定的答案,只能告诉你平均值。
先知Q*说了,从平均值来看,A股跳涨了10倍,B股票涨了两倍,C股票跌了一半,先知还告诉你实际发生的情况跟平均值并不一样,那么你该买哪只股票呢?只要你不傻,你肯定买A股票,因为先知都已经告诉你了,A股票的期望值能涨10倍的,实际结果未必是涨10倍,有可能下跌,但还有可能涨20倍。但是从期望来看还是买A股票最好。
如何理解
回到正题,该怎么理解Q*函数呢?你把Q*当成一个先知,他能告诉你每个动作带来的平均回报,你该听先知的话,选平均回报最高的那个动作,agent可以靠Q*的指点来做决策,但实际上我们并没有Q*函数,价值学习的基本想法就是学习一个函数来近似Q*。
我们把神经网络记为Q(s,a;w),神经网络的参数是W,神经网络的输入是状态S,神经网络的输出是很多数值,这些数值是对所有可能的动作的打分,每一个动作对应一个分数,我们通过奖励来学习神经网络,神经网络给动作的打分就会逐渐改进,打分会越来越准。
如果让神经网络玩几百万次超级玛丽,神经网络就跟先知一样准确了。
Dqn就是这样的一个神经网络,对于不同的问题,dqn结构可能会不一样。
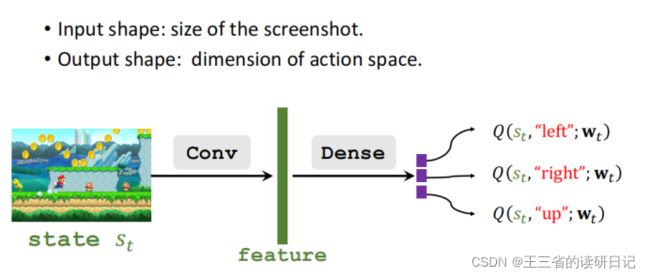
举个例子,如果是玩超级玛丽,可以把屏幕上的画面作为输入,用一个卷积层把图片变成特征向量,最后用几个全连接层把特征映射到一个输出的向量,这个输出的向量就是对动作的打分,向量每一个元素对应一个动作,在超级玛丽的例子里面有左右上三个动作,所以输出的向量是三维的。
第一个元素是dqn对向左这个动作的打分,第二个元素是对向右这个动作的打分,第三个元素是对向上这个动作的打分,假如分数是这样的,向左的分数是2000分,向右的分数是1000分,向上的动作是3000分。很显然agent应该向上跳,因为向上跳得分最高,所以只要有了dqn,把dqn训练好,就可以用dqn自动控制超级玛丽,可以打赢游戏,可以用dqn来操作agent打游戏。
具体的算法:
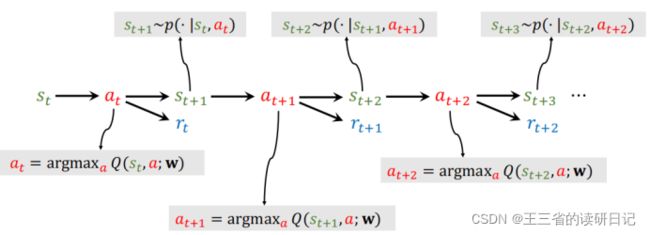
当前观测到状态St,用dqn把St作为输入,给所有的动作打分,选出分数最高的动作,作为at,agent执行at这个动作后,环境会改变状态,用状态转移函数P来随机抽一个新的状态St+1,环境还会告诉我们这一步的奖励Rt,奖励可以是正的可以是负的,也可以是0。
奖励就是强化学习中的监督信号,dqn要靠这些奖励来训练,有了新的状态St+1,dqn在对所有的动作打分,agent选择分数最高的动作作为at+1,agent执行at+1后,环境会再更新状态S,还会再给一个奖励R。
然后还是重复这个过程,让dqn给动作打分,agent选择分数最高的动作来执行,然后环境再更新状态S,再给奖励R,不断重复这个过程,一直到游戏结束。
2. TD算法
怎么训练dqn?最常用的就是TD算法。
举个例子:
我想要开车从纽约到亚特兰大,我有一个模型Q,参数是W,它可以预测出开车出行的时间开销。
我现在要从纽约出发了,模型告诉我,要开车1000分钟才能到亚特兰大,这个模型一开始不是很准确,但是随着训练次数的增加,这个模型就会越来越准。
首先出发之前让模型做一个预测,记作是q,模型告诉我从纽约到亚特兰大要花1000分钟,所以q=1000,我这就出发了。
我到亚特兰大我看一下手表,发现我其实只用了860分钟,这里的q是模型的预测,而y是真实的时间开销,于是我把y作为target,q跟y不太一样,q比y大了140分钟,这就说明我的模型预测有了偏差,比我实际的时间y要多,这就造成了loss损失。
损失定义为q和y的平方差,记作L,我们对loss L关于模型参数W求导,然后把导数用链式法则展开,L是q的函数,q是W的函数,所以L对W求导就=q对W求导,再乘上L对q求导,如上图。
结果就是q减y*q函数对W的导数,梯度求出来了,我们就可以用梯度下降来更新模型参数W,新的参数wt+1=wt-α*梯度,这里α叫做学习率或者步长,假如我们用wt+1代替wt做一次预测,那么预测值会更接近真实值,Y=860,这是因为梯度下降减少了loss,让预测值离真实值y更近了。
这种算法比较笨,必须完成整个旅途,我才能对模型做一次更新。
假设我走到一半,汽车坏了,还有没有办法对模型做一次更新?我从纽约开车去亚特兰大,我会途经美国首都Washington DC,假如我到了DC,车就抛锚了,我在DC修了三天车,假期结束了,很遗憾我没办法去亚特兰大了,我压根就没到亚特兰大。
我有没有办法利用从纽约到DC这一小段旅途来改进模型?答案是可以的,我们可以用TD算法来做这件事。
我出发的时候模型做了预测,模型说从纽约开车到亚特兰大要花1000分钟,1000就是模型的估计。
当我开车到DC的时候,我一看表发现自己已经花了300分钟了,这个300分钟是真实的观测。模型这时候又告诉我了,从DC开车到亚特兰大要花600分钟,回顾一下Q(w)=1000是模型最初的预测,也就是模型最初推测从纽约开车到亚特兰大要花1000分钟,我实际上花了300分钟开车到DC,模型告诉我还需要600分钟才能到亚特兰大。
TD target
根据模型新的预测,总时间是300+600=900分钟,比原本1000分钟的估计要快了100分钟,在TD算法里面这个新的估计900分钟,这叫做TD target。
TD target 900分钟虽然也是个估计,未必是实际情况,但是它比最初的1000分钟要更可靠,最初的估计1000分钟纯粹就是个估计,没有事实成分在里面,虽然TD target 900分钟也是个估计,但其中有事实的成分,其中300分钟就是实际的观测,当我越接近亚特兰大,TD target就越准确,越接近真实值。
要是我离亚特兰大只剩10公里了,这时候TD target跟我真实的时间开销最多就差几分钟,TD target比出发前的估计要更准确,我越接近亚特兰大,TD target也就越准。
加入用TD target,我不用跑完整个路程去知道真实的时间开销。
我到了DC算出TD target,Y=900,我就可以更新模型参数了,我假装Y=900就是真实观测ground truth。
然后把Y作为target,损失函数就是模型最初的估计Q(w)=1000,与TD target Y=900之间差 的平方。
这里最初的估计Q(w)与TD target y之间的差叫做TD error。
这里TD error=1000-900=100,然后算梯度,用loss 函数L关于W求导。
根据链式求导法则,TD error乘上Q对W的导数 ,算出来梯度,用梯度下降来更新一次模型参数,新的模型参数wt+1=wt-α×梯度。
思考一个问题,TD算法有什么道理呢?
换一个角度来理解,模型估计从纽约到亚特兰大要花1000分钟,从DC到亚特兰大要花600分钟,两者的差=400分钟。
所以我们可以这样认为,模型估计从纽约到DC要花400分钟,我开车到达DC,我一看表发现我只花了300分钟,这比预计的400分钟要快,预计时间400分钟与真实时间300分钟之间的差,这100分钟就是TD error,这跟我们之前算的TDerror完全相等,TD算法的目标是什么?TD算法的目标就是让TDerror尽量接近零,TDerror=0就意味着预计时间与实际时间相等,这是最理想的状况。
所以TD算法要用梯度下降来减小TD error。
刚才我们学了TD算法,有了TD算法,即使不完成旅途也能更新模型参数,把TD算法用来学习dqn是相同的道理,我不需要打完游戏,我就能更新dqn的参数。
如何用TD算法用来学习dqn?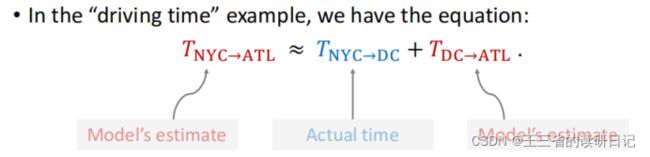
刚才的例子里面要用到这样一个公式,有这样一个公式才能使用TD算法。
左边是从纽约到亚特兰大整个旅途的时间,右边是两段分别的时间。理想情况下左右两边应该相等。
我从纽约到亚特兰大整个的时间应该=第一段纽约到DC的时间+第二段DC到亚特兰大的时间,整个旅途的时间与第二段路程的时间都是模型的估计,而第一段旅途的时间则是真实的观测。
我看了表得知从纽约到DC实际花了300分钟,想要用TD算法,必须要用类似这样的公式。
等式左边有一项,右边有两项,右边的两项中rt是真实观测到的,在深度强化学习中也有这样一个公式,等式左边是dqn在t时刻做的估计,这是未来奖励总和的期望。
这相当于纽约到亚特兰大的总时间,等式右边有一项rt,这是真实观测到的奖励,这是真实的,相当于我从纽约开车到DC真是花费了300分钟。
等式右边第二项,q(St+1,at+1;W)是dqn在t+1时刻做的估计,相当于从DC到亚特兰大的预计时间。
回顾一下discontent return,折扣回报。
根据定义折扣回报Ut可以写成这种形式。
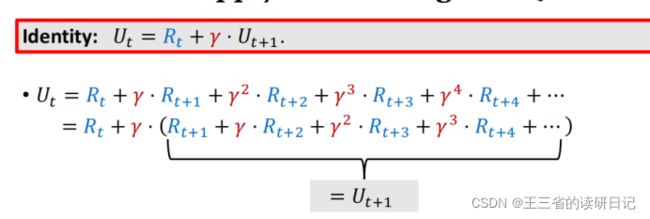
Ut=Rt+γ×Rt+1+γ²*Rt+2+γ³×Rt+3+γ^4×Rt+4....一直到结束。
这里的R是环境给的奖励,γ是一个介于0和1之间的折扣率,从第二项开始,每一项里都有γ,现在把一个γ给提取出来,这些项就可以写成γ*括号里的内容。
上面这些项消掉一个γ,就是括号里的内容,提取出γ,后面这些项写成了γ*括号里的内容,括号里的内容是什么?
再用一下折扣回报U的定义,不难发现括号里的内容就是Ut+1,在t+1时刻的discounted return,Ut+1=Rt+1+γ*Rt+2+γ²*Rt+3+γ³*Rt+4...,因此我们得到一个等式,Ut=Rt+γ*Ut+1,这个等式反映了相邻两个折扣回报之间的关系,t时刻的回报Ut=Rt+γ*Ut+1。
其中Rt 表示在t时刻的奖励,Ut+1 表示t+1时刻的回报。
现在我们要把TD算法用到dqn上,在t时刻,dqn输出的值q(St ,at;w)是对Ut作出的估计,这就像是我从纽约出发前模型做的预测,告诉我纽约到亚特兰大的总时间,在下一时刻,dqn输出的值Q(St+1,at+1;W)是对Ut+1的估计。
这就像是我开车到DC模型预测DC到亚特兰大的第二段路程的时间,我们已经知道了Ut和Ut+1存在这样一个关系,Ut=Rt+γ*Ut+1。
所以Ut的期望,≈Rt+Ut+1的期望,所以我们可以得到这样一个关系。
Dqn在t时刻做出的预测,Q(St ,at;w)≈Rt+γ*(t+1时刻做出的预测)。
左边这一项是dqn对Ut的近似,右边的是dqn对Ut+1的近似,Ut=Rt+γ*Ut+1。
类似于这个公式:
所以左边和右边比较接近,左边是在t时刻做出的估计,到了t+1时刻,我们已经真实观测到了奖励rt,Q(St+1,at+1;w)是dqn在t+1时刻做出的预计,右边这两项的加和更加接近真相,所以我们把它作为TD target。
通俗的话讲,左边prediction这一项Q就像是出发之前,模型预计从纽约到亚特兰大的总时间,右边TD target就像是我开车到了DC,用第一段的真实驾驶时间+下一段的预计时间。
有了prediction和TD target,我们就可以更新dqn的模型参数了。
在t时刻模型做出了预测,q(St ,at;Wt),这里的St是当前的状态,at是已经做出的动作,wt是当前的模型参数,到了t+1时刻,我们观测到了真实的奖励Rt,还观测到了新的状态St+1,有了状态St+1,我们就可以用dqn算出下一个动作at+1了。
在t+1时刻我们知道了Rt St+1还有at+1的值,这时候我们就可以计算TD target,记作yt,yt=rt+γ*Q(St+1,at+1;wt) 其中Q(St+1,at+1;wt)表示(t+1时刻dqn做出的预测)。
t+1时刻的动作at+1是怎么算出来的?Dqn对每一个动作打分,分数最高的动作就被选出来作为at+1。
所以Q(St+1,at+1;wt)=对Q函数关于a求最大化。
我们希望预测Q(St ,at;w)尽量接近TD target yt,我们把两者差了平方Lt作为loss,然后算Lt关于模型参数W的导数,然后做一次梯度下降来更新模型参数W。
做梯度下降的原因是为了让这个loss减小。
3. 总结:
value based reinforcement learning,价值学习。
用到了optimal action value function,动作价值函数 Q*。
首先对回报Ut求期望把除了St和at之外的随机变量全部用期望给去掉。
然后在关于策略函数π求一个最大化,去掉了π,得到了Q*函数就跟π没有关系。
Q*函数可以基于当前状态St对所有动作打分,分数就能反映每一个动作的好坏程度,只要有了Q*函数,就可以用Q*函数来控制agent运动。
每一个时刻agent只需要选出分数最高的动作,执行这个动作就好了。
然而实际上我们并没有Q*函数,价值学习的目标就是学出一个函数来近似Q*,dqn就是用一个神经网络来近似Q*函数,把 dqn记作是Q(s,a;w),这里的W是神经网络的参数,dqn的输入是观测到的状态S,比如超级玛丽游戏中的画面就是状态S,dqn的输出是对每一个动作a的打分,超级玛丽游戏中agent能做左右上三个动作,所以dqn输出就是一个3×1的向量,一开始dqn的模型参数都是随机的,agent会根据dqn的指导不断的尝试,有时获得正奖励,有时获得负奖励。
强化学习就是通过奖励来更新模型参数,让模型越来越好,怎么样通过奖励来更新模型参数。
TD算法是学习dqn最常用的算法,TD算法不断重复这个过程。
第一,关系到当前的状态St和已经执行的动作at。
第二,用dqn做一次计算,输入是状态St,输出是对动作at的打分,把输出记做qt。
第三,用反向传播对dqn求导得到梯度dt。Tensorflow和pytorch都可以自动求梯度。
第四,由于agent已经执行了动作at,环境会更新状态S,并且给出奖励Rt。
第五,有了状态St+1和奖励Rt,我们就可以用这个公式求出TD target的yt,yt=Rt+γ*新的dqn的输出。
第六,最后做一次梯度下降更新模型参数W,梯度=预测值Qt和TDtarget的Yt之间的差,再*dt,这样就完成了一次TDtarget算法迭代。每当得到一个reward Rt就可以做这样一次算法迭代,更新一次模型参数W。