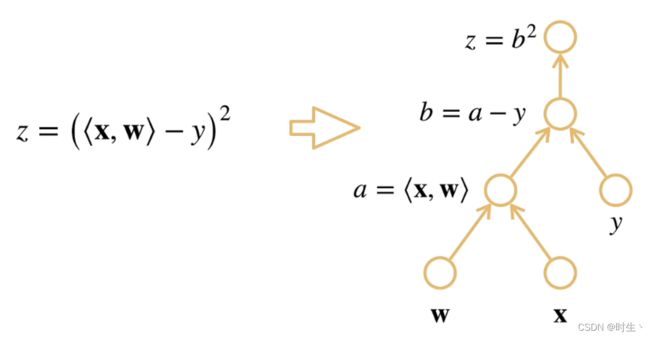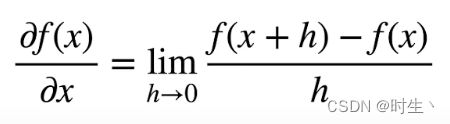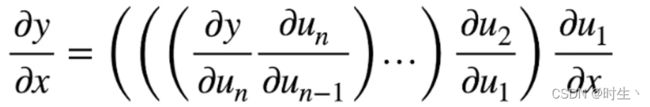动手学深度学习——矩阵求导之自动求导
深度学习框架通过自动计算导数,即自动微分(automatic differentiation)来加快求导。 实际中,根据我们设计的模型,系统会构建一个计算图(computational graph), 来跟踪计算是哪些数据通过哪些操作组合起来产生输出。 自动微分使系统能够随后反向传播梯度。 这里,反向传播(backpropagate)意味着跟踪整个计算图,填充关于每个参数的偏导数。
下面的求导计算多是采用分子布局的形式,关于分子布局和分母布局的说明可以看我的这篇文章:矩阵求导之布局分析
一、向量链式法则
- 标量链式法则
- 扩展到向量
例子1
说明:
- 采用分子布局计算
例子2
说明:
- 对于一个
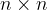 的单位矩阵,可以表示为
的单位矩阵,可以表示为 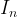 或
或 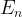 ,也可以简单表示为
,也可以简单表示为 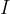 或
或 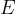 。
。 - 采用分子布局计算
二、计算图
- 将代码分解成操作子
- 将计算表示成一个无环图
1. 显示构造
- Tensorflow、Theano、MXNet;
- 手动一步步构造公式(生成计算图),然后再将数值代入公式中计算,一般数学上解决问题都是属于显示构造。
2. 隐式构造
- PyTorch、MXNet;
- 将函数和变量值都交给框架,由框架在后台生成计算图并计算梯度;
- 其中autograd模块用于自动求解梯度。
三、自动求导
四、两种累积模式
- 以链式法则为例,说明正向累积与反向累积的区别:
1. 正向累积(正向传递)
- 从最外层开始计算,得到结果后保存,再代入内一层的求导公式与该结果继续计算,重复直到求出原式的梯度:
2. 反向累积(反向传递)
- 从最内层开始计算,得到结果后直接与外一层的求导公式继续计算,重复直到求出原式的梯度:
- 这里只是以链式法则为例展示正向与反向两种累积模式的区别,一般来说:
- 正向累积的思想多用于复合函数正向计算函数值;
- 反向累积的思想多用于复合函数各层逆向求导数;
- 通常使用先正向-后反向来解决实际问题。
3. 正向计算与反向求导
- 构造计算图:
正向:从下(外层)往上(内层)执行图,需要存储中间结果,且不能剪“枝”——参数后续有用;
反向:从相反方向执行图,当层计算完后,就可以去除不需要的“枝”——已经使用完的参数;
- 流程举例:
1)左图中演示的是正向传播计算过程:
- 先从底层开始计算
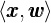 的值,得到的中间结果
的值,得到的中间结果  并保存,其中“枝”
并保存,其中“枝” 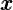 和
和 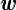 需要留下;
需要留下; - 然后开始计算上一层
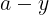 的值,代入
的值,代入  的值后得到中间结果
的值后得到中间结果  并保存,其中“枝”
并保存,其中“枝”  需要留下;
需要留下; - 最后计算顶层
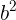 的值, 代入
的值, 代入  的值后得到最终结果
的值后得到最终结果 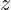 并保存;
并保存; - 最终求得并保存了中间值
 和
和  以及函数值
以及函数值 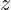 ,以供后续求导使用。
,以供后续求导使用。
2)右图中演示的是反向传播求导过程:
- 先从顶层开始计算
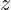 对
对 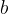 的偏导式,得到的结果
的偏导式,得到的结果  后,将保存的中间值
后,将保存的中间值  代入求得梯度值
代入求得梯度值 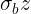 ;
; - 再计算下一层
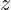 对
对  的偏导式,得到的结果
的偏导式,得到的结果  ,由于
,由于 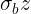 已知且结果与中间值
已知且结果与中间值  和“枝”
和“枝”  无关,固求得梯度值
无关,固求得梯度值 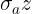 ;
; - 然后计算最底层
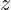 对
对 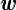 的偏导式,得到的结果
的偏导式,得到的结果 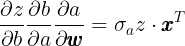 ,由于
,由于 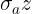 已知,再代入“枝”
已知,再代入“枝” 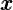 便可求得最终的梯度值
便可求得最终的梯度值 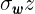 ;
; - 过程中下一层的梯度计算直接累积在上一层的梯度值中,不需要保存后再代入,同时当前层使用完的“枝”可以剪去。
4. 复杂度分析
正向累积(正向传播):
- 计算复杂度:O(n),n是操作子个数(类别计算图中层数);
- 通常正向和反向的代价类似;
- 内存复杂度:O(n),因为需要存储正向的所有中间结果。
反向累积(反向传播):
- 计算复杂度:O(n),每一个变量计算一次梯度;
- 内存复杂度:O(1),从头到尾依次计算结果。
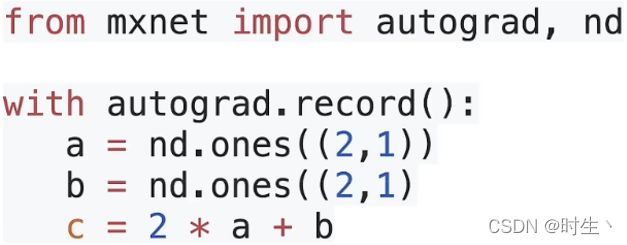
五、代码实现自动求导
PyTorch中主要使用的求梯度方法是反向传播
1. 标量函数的反向传播
一个简单的例子:假设我们想对函数 ![]() 关于列向量
关于列向量 ![]() 求导。
求导。
1)首先,我们创建 变量x 并为其分配一个初始值:
import torch
x = torch.arange(4.0)
x| tensor([0., 1., 2., 3.]) |
2)为 变量x 分配一块内存空间来存储梯度:
注意,我们不会在对一个参数的每次求导时都分配新的内存, 因为我们经常会成千上万次地更新相同的参数,每次都分配新的内存可能很快就会将内存耗尽;
注意,一个 标量函数 关于 向量x 的梯度是向量,并且与x具有相同的形状。
x.requires_grad_(True) # 等价于x=torch.arange(4.0,requires_grad=True)
# 实质是申明变量x需要计算梯度,因此框架会为其分配空间
print(x.grad) # 默认值是None| None |
3)计算 函数y 的值:
- x 是一个长度为4的向量,计算 x 和 x 的内积,得到了我们赋值给 y 的标量输出。
y = 2 * torch.dot(x, x) # 1*1+2*2+3*3+4*4=28
y| tensor(28., grad_fn= |
4)接下来,我们通过调用反向传播函数 backward 来自动计算 y 关于 x 每个分量方向上的梯度值,并调用 x 的 grad 属性打印这些梯度:
- 函数
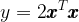 关于 x 的梯度应为 4x。
关于 x 的梯度应为 4x。
y.backward() # 反向传播计算梯度
x.grad # 查看计算的梯度值| tensor([ 0., 4., 8., 12.]) |
5)验证梯度正确性:
x.grad == 4 * x| tensor([ 0., 4., 8., 12.]) |
6)紧接着计算关于 变量x 的另一个函数:
- 在默认情况下,PyTorch会将新梯度的累加在上一次计算的梯度上,所以我们需要调用 zero_ 方法将梯度值清零。
x.grad.zero_()
y = x.sum() # 0+1+2+3=6
print(y,x.grad)| tensor(6., grad_fn= |
- 可以看到梯度已经被清零,并且我们这里利用 sum 将 向量y 变成了 标量y 后再求梯度,此时函数
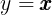 关于 x 的梯度应为和x形状相同的 全1向量 ;
关于 x 的梯度应为和x形状相同的 全1向量 ; - 至于为什么不直接对 向量y 反向传播求梯度,将在下一部分展开讨论。
y.backward()
x.grad| tensor([1., 1., 1., 1.]) |
2. 非标量函数的反向传播
当 函数y 不是标量时,向量y 关于 向量x 的导数的最自然解释是一个矩阵;
我们可以采用下面两种方式调用 backward ,正常求得梯度:
backword内存在一个权重参数,这个参数的长度对应输出的个数,元素值为每个输出对与其相关的输入求导后的权重值;
- backword在不手动设置权重参数时,默认值是标量1 ,表明只有一个输出项,且 该输出项 在对 与它相关的输入项 求梯度后,所得的结果*权重值1即可。因此我们可以使用sum函数来将向量函数y转换为标量函数,即将输出项的个数变为1。
- 我们自己指定backword的权重参数时,需要考虑的就是输出项的个数,以及我们希望每个输出项求得的梯度应当附加的权重值。
x.grad.zero_()
y = x * x # 注意这里不是内积运算,而是x内每个元素求平方,运算结果是一个向量
print(y) # 此时y是一个向量
y.sum().backward() # 等价于y.backward(torch.ones(len(x)))
# torch.ones(len(x)):生成与x长度相同的全1张量
x.grad| tensor([0., 1., 4., 9.], grad_fn= tensor([0., 2., 4., 6.]) |
下面用 ![]() 的情况来简单演示上面求梯度的原理(
的情况来简单演示上面求梯度的原理( ![]() 太占篇幅啦!):
太占篇幅啦!):
 注意:backward的权重参数是我们为相关输入项整体的梯度附上的权重,与神经网络计算输出值时使用的权重不一样!
注意:backward的权重参数是我们为相关输入项整体的梯度附上的权重,与神经网络计算输出值时使用的权重不一样!
x.grad.zero_()
y = x * x
y.backward(torch.ones(len(x)))
print(x.grad)
x.grad.zero_()
y = x * x
y.backward(torch.tensor([1,2,3,4]))
print(x.grad)
x.grad.zero_()
y = x * x
y.sum().backward(torch.tensor(10))
print(x.grad)| tensor([0., 2., 4., 6.]) tensor([ 0., 4., 12., 24.]) tensor([ 0., 20., 40., 60.]) |
3. 分离计算
有时,我们希望将某些计算移动到记录的计算图之外。 例如:
假设 y 是作为 x 的函数计算得到的;而 z 则是作为 y 和 x 的函数计算得到的;想象一下,我们想计算 z 关于 x 的梯度,但由于某种原因,我们希望将 y 视为一个常数, 并且只考虑到 x 在 y 被计算后发挥的作用。
在这里,我们可以使用 detach 分离 y 来返回一个新变量 u,该变量与 y 具有相同的值, 但 u 丢弃了计算图中如何计算 y 的全部信息。 换句话说,梯度不会向后流经 u 到 x。 因此,下面的反向传播函数 backward 计算 z=u*x 关于 x 的偏导数,同时将 u 作为常数处理, 而不是 z=x*x*x 关于 x 的偏导数。
x.grad.zero_()
y = x * x
u = y.detach()
z = u * x
z.sum().backward()
x.grad == u| tensor([True, True, True, True]) |
但 y 任然保留了自身的计算结果,我们可以随后在 y 上调用反向传播函数, 得到 y=x*x 关于的 x 的导数,即 2*x。
x.grad.zero_()
y.sum().backward()
x.grad == 2 * x| tensor([True, True, True, True]) |
4. Python控制流中的梯度计算
Pytorch使用自动微分的一个好处是: 即使构建函数的计算图需要通过Python控制流(例如,条件、循环或任意函数调用),我们仍然可以计算得到的变量的梯度。
- 在下面的代码中,while 循环的迭代次数和 if 语句的分支选取,都取决于输入 a 的值:
def f(a):
b = a * 2
# norm用于求范数,ord参数默认为2,即求第二范数
while b.norm() < 1000:
b = b * 2
if b.sum() > 0:
c = b
else:
c = 100 * b
return c- 调用函数对 标量a 进行计算,通过反向传播获取函数的梯度:
a = torch.randn(size=(), requires_grad=True) # 生成一个随机整数a,申明需要计算梯度
d = f(a)
d.backward()- 在我们定义的 f 函数中,对 a 的计算是线性分段的,在每个python控制流下执行的线性计算都会被框架记录到计算图当中;
- 换而言之,对于任何 a ,存在某个常量标量 k ,使得 f(a)=k*a ,其中 k 的值取决于输入 a;因此,我们可以直接用 d/a 验证梯度计算是否正确。
a.grad == d / a| tensor(True) |
- 当 a 是一个向量时,由于 f(a)=k*a 导致函数d也变成了向量,则需要在反向传播时传入参数:权重张量;或用sum函数将d变为标量(详见2中分析):
a = torch.randn(size=(4,),requires_grad=True)
print(a)
d = f(a)
d.backward(torch.ones(len(a))) # 或d.sum().backward()
a.grad == d / a| tensor([-0.8285, -0.1860, -0.2410, -0.1880], requires_grad=True) tensor([True, True, True, True]) |
六、练习部分
题5:使 f(x)=sin(x),绘制 f(x) 和 df(x)/dx 的图像,其中后者不使用 f′(x)=cos(x) 。
import torch
import matplotlib.pyplot as plt
x = torch.arange(-4000,4000)/1000
x.requires_grad=True
# 绘制函数:y=sin(x)
y = torch.sin(x)
plt.plot(x.detach().numpy().reshape(-1,1),y.detach().numpy().reshape(-1,1))
# 绘制导数:dy/dx=cos(x)
y.backward(torch.ones(len(x)))
plt.plot(x.detach().numpy().reshape(-1,1),x.grad.detach().numpy().reshape(-1,1))
plt.legend(["sin(x)","cos(x)"])
plt.show() |