今天学了关于树的最最最最基本的有关概念和性质,做一下简单的记录:
首先,树是什么???
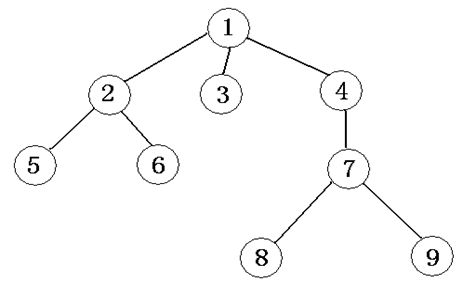
其实简单点来说,树就相当于一个元素之间有确定关系的集合。其中每个元素都是一个结点,他们两两以特定的方式连接并相互关联,而树就是由递归定义与实现的。例如,下图就是一个典型的树:
其中,元素1~9都是结点,而1上面没有结点与它连接,所以它就是一个特殊的结点——树根。
除了根结点,其他的结点能分成很多个互不相交的有限集合,而其中的几个互相连接的结点元素就可以组成一棵子树。
每一个结点的子树的个数,叫做这个结点的度,其实这个结点连接的有几个子结点它的度就是几,比如图中的4,他就有1个子节点,所以它的度就是1,而3下面没有跟它连接的子结点,所以它的度就是0。
特别的,如果这个结点的度是0,那这个结点就叫做叶节点,如图中的5,6,3,8,9就都是叶结点。
上面的结点是下面结点的父节点,下面的是上面的子结点,有相同父节点的子结点互为兄弟结点。
下面来道水题练练手:
要求先输入两个数 n、m,表示一棵树的结点数和边数,再输入m行,每行输入一个父节点 x 和一个x的子结点 y。现在要求输出树根,子结点最多的结点 和 此节点的子结点。(数据范围忽略)
思路其实就是桶的思想,先输入每个x和y,并记录y的父节点x。全部输入完之后再判断,如果没有父节点,那这个点就是树根。最后再用一个循环嵌套遍及每一个结点,记录他子结点的个数,找出最大值就好了。
代码如下:
1 #include2 using namespace std; 3 int n,m; 4 int tree[100]={0};//记录父节点 5 int ans,sum,maxn; 6 int main() 7 { 8 int x,y; 9 scanf("%d%d",&n,&m); 10 for(int i=1;i<=m;i++){ 11 scanf("%d%d",&x,&y); 12 tree[y]=x; 13 } 14 for(int i=1;i<=m;i++){ 15 if(tree[i]==0){ 16 printf("%d\n",i); 17 break; 18 } 19 } 20 for(int i=1;i<=n;i++){ 21 sum=0; 22 for(int j=1;j<=n;j++){ 23 if(tree[j]==i) sum++; 24 if(sum>maxn){ 25 maxn=sum; 26 ans=i; 27 } 28 } 29 } 30 printf("%d\n",ans); 31 for(int i=1;i<=n;i++){ 32 if(tree[i]==ans){ 33 printf("%d ",i); 34 } 35 } 36 return 0; 37 }
关于树的遍历,有好几种:
1、先序遍历:先访问根结点,再从左往右的访问每一棵子树,与DFS相似,在上图中遍历顺序就是125634789
2、后续遍历:先从左到右先遍历每一棵子树,最后访问根结点,在上图中遍历的顺序就是562389741
3、层次遍历:一层一层地遍历,在图上遍历的顺序就是123456789
4、叶结点遍历:上图按照这个思想访问的结果为:56389;
5、中序遍历:左儿子——父节点——右儿子(前提是必须是二叉树)。
关于二叉树:
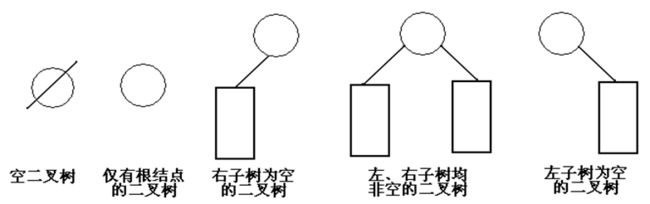
二叉树是一种特殊的树形结构,除了叶节点,其余的每个节点的度都小于等于2,也就是说每个父节点都最多有两个子结点。下图是二叉树的五种形态:
关于二叉树的性质:
1、在二叉树的第i层上最多有 2 的 i-1 次方个结点
证明:二叉树的第一层至多有2的零次方个结点,第2层至多有2的一次方个结点,因为每个节点最多有两个儿子,所以每一层都是上一层的结点数乘2,那第 i 层自然就是2^(i-1)个结点。
2、层数(深度)为k的二叉树最多有 2^k -1个结点
证明:由于第1层有2^0个结点,第2层有2^1个结点,那第k层至多有2^(k-1)个结点,
则总结点数就是:2^0+2^1+……+2^(k-1)=2^0+2^0+2^1+……+2^(k-1)-2^0=2^1+2^1+2^2+……+2^(k-1)-1=2^k -1
3、如果一棵二叉树叶结点数为n0,度为2的结点数为n2,则一定满足:n0=n2+1
证明:对于父节点一定对应两子结点的子树,设一共x层,那非子结点的个数就是前x-1层的个数,由性质2得出前x-1层的个数为2^(x-1)-1,由性质1得出第x层上的子结点个数为2^(x-1)个,所以两者相差1。
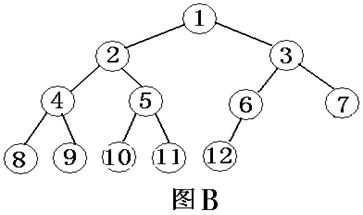
4、有n个结点的完全二叉树(最下层的叶节点左边是满的,右边可以为空,如下图)的深度为:floor(log2 n)+1
证明:设结点数是n,深度是k,由性质2得:n=2^(k-1)为指数函数,转换成对数函数就是:log2 n=k-1。即 k=floor((log2 n)+1),由于人家不一定是满的,要加一个下取整。
5、对于任意的完全二叉树的某个标号为n的左结点,此结点的父节点的标号为n/2,兄弟结点的标号n+1,左儿子为2n,右儿子为2n+1。
一道简单的练习题:
q:一棵完全二叉树的结点总数是18,其叶节点数是?
a:由性质4得出此二叉树的层数为floor(log2 18)+1=5
由性质2的前4层(由于是完全二叉树,前4层一定是满的)的结点数是2^4 -1=15
所以最后一层有18-15=3个结点,最后一层的三个子结点用掉了上一层的2个父结点
第四层有2^(4-1)=8个子结点,用掉俩还剩6个没有子结点的结点,他们也是叶结点
所以一共有3+6=9个子结点
遍历二叉树的代码实现:
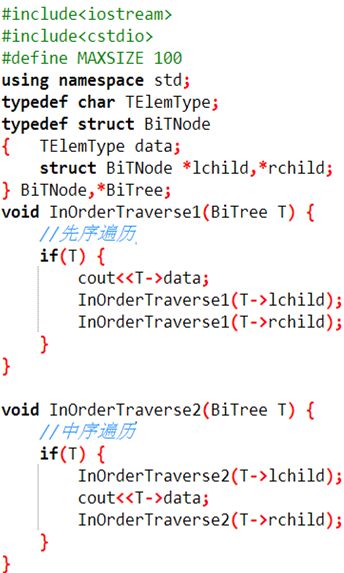
1.先序遍历:先访问根结点,再遍历左二叉树,最后遍历右二叉树。
1 void preorder(tree bt) //先序递归算法 2 { 3 if(bt) 4 { cout << bt->data; 5 preorder(bt->lchild); 6 preorder(bt->rchild); 7 } 8 }
2、中序遍历:先遍历左二叉树,再访问根结点,最后遍历右二叉树。
1 void inorder(tree bt) //中序遍历递归算法 2 { 3 if(bt) 4 { inorder(bt->lchild); 5 cout << bt->data; 6 inorder(bt->rchild); 7 } 8 }
3、后序遍历:先遍历左二叉树,再遍历右二叉树,最后访问根结点。
1 void postorder(tree bt) //后序递归算法 2 { 3 if(bt) 4 { 5 postorder(bt->lchild); 6 postorder(bt->rchild); 7 cout << bt->data; 8 } 9 }
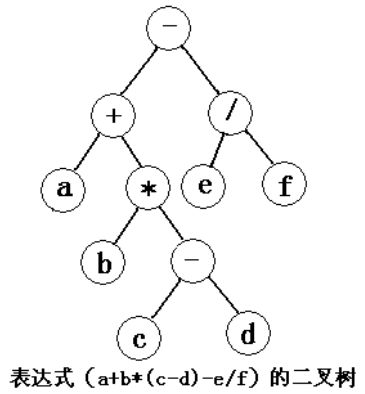
关于一棵表达式树,可以分别用先序,中序,后序遍历方法得到3钟不同的遍历结果:
前缀表示(波兰式):- + a * b - c d / e f
中缀表示:a + b * ( c - d ) - e / f
后缀表示(逆波兰式):a b c d - * + e f / -
还有就是关于二叉树的唯一性:
知道先序或后序其中的一个和中序就可以确定一棵树,但是只知道先序和后序就不可以·,比如:
二叉树基操:
1、建树
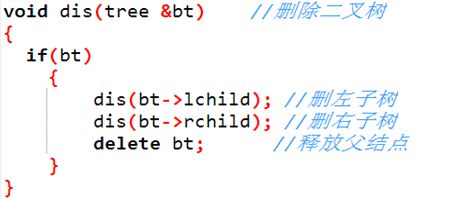
2、删树
3、插点
我来模拟一下,假设现在我有一个排好序了的二叉树,排序规则是对于任意一个子树根,他的左子树上的结点都比子树根小,右子树上的结点都比它大。
那我现在就用一个递归,如果输入的数比根结点小那就递归左子树,如果大就递归右子树,直到找到合适的位置就把他加进去
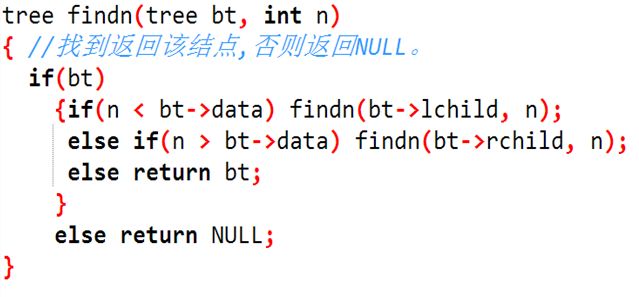
4、查找
其实也跟插点的思想差不多,类似于二分查找,找到就返回该点,找不到就返回NULL
来几道题练练手吧
注意!!下面的操作均用到指针!!!
【问题描述】
由于先序、中序和后序序列中的任一个都不能唯一确定一棵二叉树,所以对二叉树做如下处理,将二叉树的空结点用·补齐,称为原二叉树的扩展二叉树,扩展二叉树的先序和后序序列能唯一确定其二叉树。
现给出扩展二叉树的先序序列,要求输出其中序和后序序列。
【输入样例】
ABD..EF..G..C..
【输出样例】
DBFEGAC
DFGEBCA
题解如下:
【问题描述】
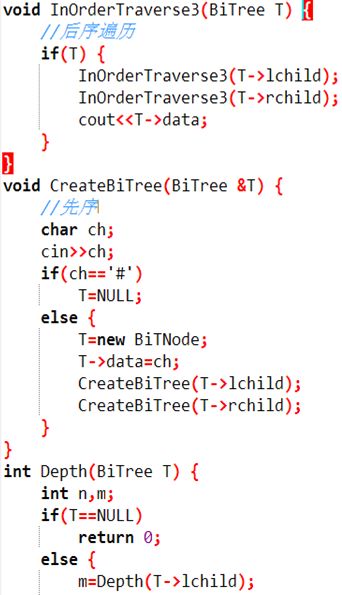
以二叉链表作存储结构,建立一棵二叉树,并输出该二叉树的先序、中序、后序遍历序列、高度和结点总数。
【输入样例】
12##3## //#为空
【输出样例】
123 //先序
213 //中序
231 //后序
2 //高度
3 //结点总数
题解如下:
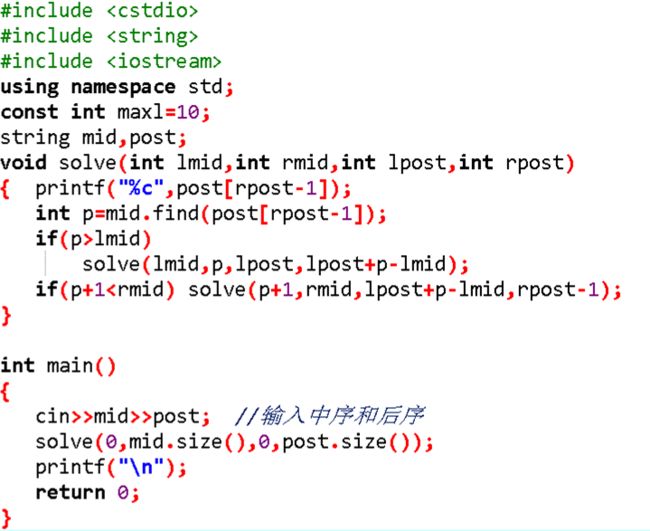
[题目描述]
给出一棵二叉树的中序与后序排列。求出它的先序排列。(约定树结点用不同的大写字母表示,长度<=8)。
【输入格式】
2行,均为大写字母组成的字符串,表示一棵二叉树的中序与 后序排列。
【输出格式】
1行,表示一棵二叉树的先序。
【输入样例】
BADC
BDCA
【输出样例】
ABCD
题解如下:
反正我是学不懂了,就先记录到这吧
拜拜!!!