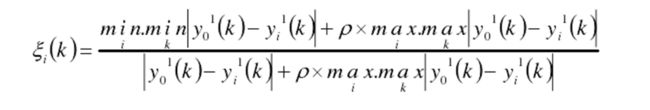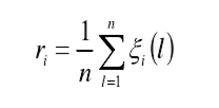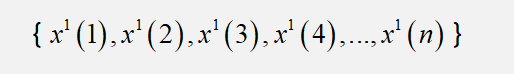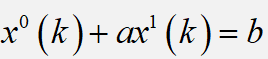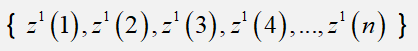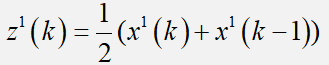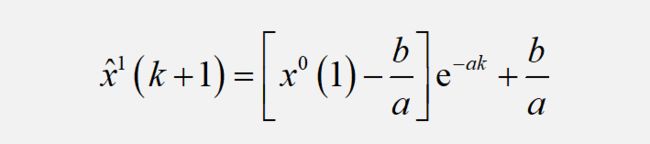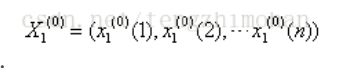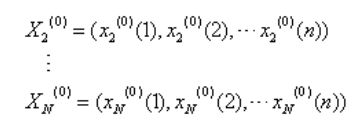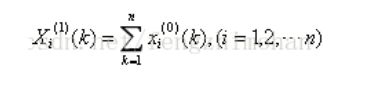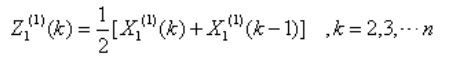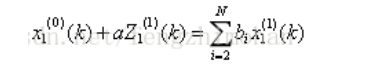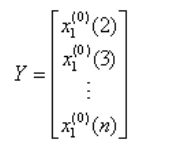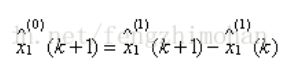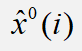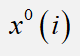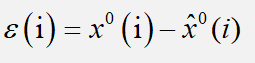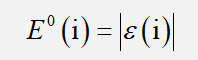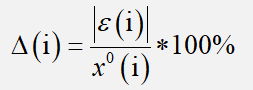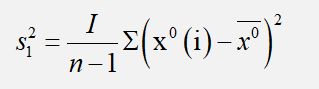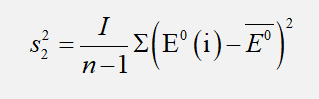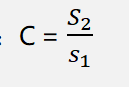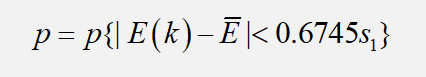灰色关联以及灰色预测GM(1,n)，GM(1,1)模型（Python实现）

**灰色关联以及灰色预测GM(1,n)，GM(1,1)模型**

简介：本篇文章简单的介绍灰色关联以及灰色预测模型，使用python代码进行实现。

1. 灰色系统的概论

2. 关于灰色关联度那些事

3. GM(1,1)模型简介以及相关实现

4. GM(1,N)模型简介以及相关实现、

5，模型检验

一、灰色系统概论

a 、概念来源：

灰色系统理论(Grey System Theory)的创立源于20世纪80年代。邓聚龙教授在1981年上海中-美控制系统学术会议

上所作的“含未知数系统的控制问题”的学术报告中首次使用了“灰色系统”一词。

b、什么是黑白灰系统：

        白色系统：发展规律明显、系统信息完全充分、系统内部特征完全已知。比如时间，速度，距离的关系式子V= S/T，这里清晰的表达出了三者之间的关系，以及我们完全明白其中的关系。

 黑色系统：内部信息对于外界来说一无所知的。举例：有一天你经过你盆友家门口，同时也有一辆车经过这时你朋友家的狗疯狂的往房间里跑。这时候狗狗的行为举动对于你来说就是一个黑箱，你不明白其中的相关因素。

灰色系统：部分信息已知，部分未知，同时系统内各因素关系不确定。例子：接着上述，这只狗的行为对于你的朋友来说就是一个灰箱，他知道狗狗之前被车子压过。但是他不清楚是否和其他的因素有关联，比如：车的大小，车的类型等等。

c、灰色系统的研究对象

其研究对象有连个特点：部分信息已知，部分信息未知的“小样本”  以及 “贫信息”不确定系统

二、有关灰色关联的那些事

a、为什么要使用灰色关联分析

一般的抽象系统：如：社会系统、经济系统等包含许多种的因素，我们希望知道哪些因素是主要的，哪些对系统的影响程度较小，因此我们可以知道去促进哪些因素，不考虑那哪些因素。

b、基本的思想

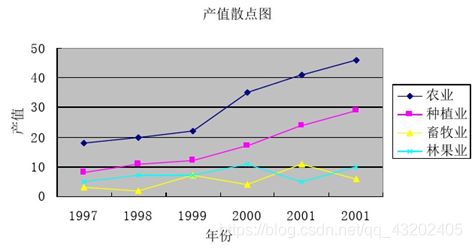
关联度分析方法-即根据因素之间发展态势的相似或相异程度来衡量因素间关联的程度，它揭示了事物动态关联的特征与程度。他同时液也是根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近，相应序列之间关联度就越大，反之就越小。可以看下图，我们可以知道对于某地农业的总产值来说，种植业与农业产值关联程度较高。（图片来自他人博客）

                                                    

c、关联度计算

例如：我们要计算汽车碳排放，火灾次数，化工厂的数量这三个因素对于空气质量的影响的关联的程度。

首先我们将空气质量序列记为 X0，汽车碳排放序列，火灾次数序列，化工厂数量序列，分别记作X1,X2,X2。 这里我们将Y0视作我们的母序列（这里先记住这个母序列的概念），X1,X2,X3视作我们的子序列。

然后，因为汽车碳排放，火灾次数，化工厂数量这些因素的单位不不统一，我们需要对数据进行一些预处理，也就是进行无量纲化。这里无量纲化的方法有：初值化处理，均值化处理等等。初值化处理就是每个序列当中的数值除以每个序列的第一个值，所计算的结果组成一个新的序列。均值化处理就是每个序列除以序列的均值，所计算的结果组成一个新的序列。

这里我们经过预处理的母序列记作Y0，子序列分别记作Y1,Y2,Y3，我们计算 P = | Y0 - Yi |，（这里表示的是计算子序列与母序列的差）。这个P便是其绝对误差。我们将关联系数定义为如下的公式：

 

这里我们可以看的出分子便是min.minP（两级最小差，在求出一次最小值序列中再求一次最小值） 与 max.maxP（两级最大值，在求出一次最大值序列中再求一次最大值）  ，分母是 P 与 max.maxP （由于html的公式编辑不会使用，应用网络的公式）。ρ∈(0,∞)，称为分辨系数。ρ越小，分辨力越大，一般ρ的取值区间为 (0,1),具体取值可视情况而定。当ρ ≤ 0.5463 时，分辨力最好，通常取ρ = 0.5 。

最后我们计算子序列与母序列的关联度，这里将关联度的公式定义为：

                                                             

 根据各个因素的关联度排序，关联度的值越大，说明，影响程度越大。到此关联度计算完毕。

实现代码为（代码为借鉴代码）：

数据：

                                    

# 进行关联度的分析
import pandas as pd
import numpy as np
x=pd.read_excel('data.xlsx')
x=x.iloc[:,1:].T
print("导入的数据\n",x)

# 1、数据均值化处理，进行无量纲化（消除单位不统一的因素）
x_mean=x.mean(axis=1)# 求出每一行的均值
for i in range(x.index.size):# x.index.size = 4
    x.iloc[i,:] = x.iloc[i,:]/x_mean[i]
print("均值化处理后的结果\n",x)
# 2、提取参考队列和比较队列
ck=x.iloc[0,:]
print("参考队列-即母序列\n",ck)
cp=x.iloc[1:,:]
print("比较队列-即子序列\n",cp)

# 比较队列与参考队列相减
t=pd.DataFrame()# 创建一个空表
for j in range(cp.index.size):# cp.index.size = 3
    temp=pd.Series(cp.iloc[j,:]-ck)
    t=t.append(temp,ignore_index=True)
print("做差以后的数据",t)
#求最大差和最小差
mmax=t.abs().max()
print("mmax:\n",mmax)
mmin=t.abs().min().min()
print("mmin:",mmin)
rho=0.5


#3、求关联系数
ksi=((mmin+rho*mmax)/(abs(t)+rho*mmax))
print("关联系数ksi:\n",ksi)


#4、求关联度
r=ksi.sum(axis=1)/ksi.columns.size
print("关联度r\n",r)

#5、关联度排序，得到结果r3>r2>r1
result=r.sort_values(ascending=False)
print("排序结果：\n",result)

 

三、GM(1,1)模型简介以及相关实现

   a、简介

GM(1,1)表示的是模型是一阶的，包含一个变量的灰色模型。同时通过以时间序列为基准通过对原始数据采用微分拟合的方式建立预测模型。

b、生成数简单介绍

假设有这样的一段序列存在{ x1,x2,x3,x4,x5,x6,x7}

1. 累加生成：则累加生成的序列便是{x1,x1+x2,x1+x2+x3,........}相当于累加。一次累加也被称为（1-AGO）
2. 累减生成：就是累加生成的相反操作，与其是互逆序列算子
3. 邻值生成：Z(k) = 1/2( X(k) - X(k-1 ) ),(K>=2)

C、预测模型得到过程

1. 原始形式

设 我们有序列：

                      

通过一次累加之后得到我们的1-AGO序列：

                      

这样我们称：           为GM(1,1)模型的原始形式   。

2. 基本形式

设 我们有序列：

                                  

其中：

                                             

称其为邻值生成序列。

故     为GM(1,1)模型的基本形式。（下面的图片是我们求解结果）

                       

3. 微分方程形式

根据前面得到的一次累加序列以及邻值生成序列，这里称 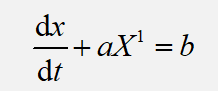     为灰色微分方程也就是  

的白化方程。

其中：a 称为发展灰数，b称为内生控制灰数。

求解微分方程，得到预测模型：

最后我们的预测值序列需要将上述的X-hat做一次累减序列进行还原。到此，GM（1，1）模型结束。

代码实现：

# 在这里测试GM(1,1)模型
import numpy as np
import math as mt
import matplotlib.pyplot  as plt

# 1.我们有一项初始序列X0
X0 = [15,16.1,17.3,18.4,18.7,19.6,19.9,21.3,22.5]

# 2.我们对其进行一次累加
X1 = [15]
add = X0[0] + X0[1]
X1.append(add)
i = 2
while i < len(X0):
    add = add+X0[i]
    X1.append(add)
    i += 1
print("X1",X1)

# 3.获得紧邻均值序列
Z = []
j = 1
while j < len(X1):
    num = (X1[j]+X1[j-1])/2
    Z.append(num)
    j = j+1
print("Z",Z)

# 4.最小二乘法计算
Y = []
x_i = 0
while x_i < len(X0)-1 :
    x_i += 1
    Y.append(X0[x_i])
Y = np.mat(Y).T
Y.reshape(-1,1)
print("Y",Y)

B = []
b = 0
while b < len(Z) :
    B.append(-Z[b])
    b += 1
print("B:",B)
B = np.mat(B)
B.reshape(-1,1)
B = B.T
c = np.ones((len(B),1))
B = np.hstack((B,c))
print("c",c)
print("b",B)

# 5.我们可以求出我们的参数
theat = np.linalg.inv(B.T.dot(B)).dot(B.T).dot(Y)
a = theat[0][0]
b = theat[1]
did = 15.41559771/-0.04352981
print(theat)
print(type(theat))

# 6.生成我们的预测模型
F = []
F.append(X0[0])
k = 1
while k < len(X0):
    F.append((X0[0]-did)*mt.exp(-a*k)+did)
    k += 1
print("F",F)

# 7.两者做差得到预测序列
G = []
G.append(X0[0])
g = 1
while g

 

四、GM(1,N)模型的简介与相关实现

简介： 这里GM(1,N)模型与GM(1,1)的原理差不多，不同之处在于输入数据有N个的变量（下面的过程整理来自于

sudo-wang的博客，相关文章链接放于文章末尾，可自行观看）

a、数据准备：

设 系统有特征数据序列（母序列）：

                                                       

       相关因素序列（子序列）：

                                                       

b、计算累加序列，邻值生成序列

1、令     的1-AGO序列为 ，其中：

                                         

2、生成    紧邻均值序列    ，其中：

                                   

称

                                   

         为GM(1,n)模型。

         在GM(1,n)模型中，a被称为发展系数，称为驱动系数，称为驱动项。

3、令B 与 Y 分别为：

 

再令，由最小二乘参数估计可得，当近似时间相应式为：

最后我们的预测值将其做累减还原（下式）可以得到我们的预测结果

                                              

代码实现：

import numpy as np
import math as mt
import matplotlib.pyplot as plt
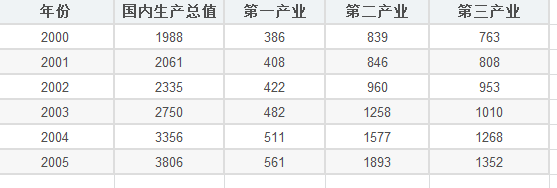
# 1.这里我们将 a 作为我们的特征序列 x0,x1,x2,x3作为我们的相关因素序列
a = [560823,542386,604834,591248,583031,640636,575688,689637,570790,519574,614677];
x0 = [104,101.8,105.8,111.5,115.97,120.03,113.3,116.4,105.1,83.4,73.3]
x1 = [135.6,140.2,140.1,146.9,144,143,133.3,135.7,125.8,98.5,99.8]
x2 = [131.6,135.5,142.6,143.2,142.2,138.4,138.4,135,122.5,87.2,96.5]
x3 = [54.2,54.9,54.8,56.3,54.5,54.6,54.9,54.8,49.3,41.5,48.9]

# 2.我们对其进行一次累加
def AGO(m):
    m_ago = [m[0]]
    add = m[0] + m[1]
    m_ago.append(add)
    i = 2
    while i < len(m):
        # print("a[",i,"]",a[i])
        add = add+m[i]
        # print("->",add)
        m_ago.append(add)
        i += 1
    return m_ago

a_ago = AGO(a)
x0_ago = AGO(x0)

x1_ago = AGO(x1)
x2_ago = AGO(x2)
x3_ago = AGO(x3)

xi = np.array([x0_ago,x1_ago,x2_ago,x3_ago])
print("xi",xi)



# 3.紧邻均值生成序列
def JingLing(m):
    Z = []
    j = 1
    while j < len(m):
        num = (m[j]+m[j-1])/2
        Z.append(num)
        j = j+1
    return Z
Z = JingLing(a_ago)
# print(Z)

# 4.求我们相关参数
Y = []
x_i = 0
while x_i < len(a)-1 :
    x_i += 1
    Y.append(a[x_i])
Y = np.mat(Y).T
Y.reshape(-1,1)
print("Y.shape:",Y.shape)

B = []
b = 0
while b < len(Z) :
    B.append(-Z[b])
    b += 1
B = np.mat(B)
B.reshape(-1,1)
B = B.T
print("B.shape:",B.shape)
X = xi[:,1:].T
print("X.shape:",X.shape)
B = np.hstack((B,X))
print("B-final:",B.shape)

# 可以求出我们的参数
theat = np.linalg.inv(B.T.dot(B)).dot(B.T).dot(Y)
# print(theat)
al = theat[:1,:]
al = float(al)
# print("jhjhkjhjk",float(al))
b = theat[1:,:].T
print(b)
print("b.shape:",b.shape)
b = list(np.array(b).flatten())


# 6.生成我们的预测模型
U = []
k = 0
i = 0
# 计算驱动值
for k in range(11):
    sum1 = 0
    for i in range(4):
        sum1 += b[i] * xi[i][k]
        print("第",i,"行","第",k,'列',xi[i][k])
        i += 1
    print(sum1)
    U.append(sum1)
    k += 1
print("U:",U)

# 计算完整公式的值
F = []
F.append(a[0])

f = 1
while f < len(a):
    F.append((a[0]-U[f-1]/al)/mt.exp(al*f)+U[f-1]/al)
    f += 1
print("F",)

# 做差序列
G = []
G.append(a[0])
g = 1
while g

五、关于模型检验

1.残差检验

根据上面我们得到预测值         ，计算我们的原始序列     与         

的绝对误差序列以及相对误差序列

a.残差序列：

b.绝对误差：

c.相对误差：

我们一般需要将平均相对误差控制在百分之0.5以内

2. 后验差检验

a. 计算原始序列的标准差：

                                                             

 

b. 计算绝对误差序列的标准差：

                                                      

 

c. 计算方差比：

 

                                                                        

 

d. 计算小概率误差：

                                                 

3、结果比对

参考文章链接：

https://blog.csdn.net/wuli_dear_wang/article/details/80587650

https://blog.csdn.net/qq_29831163/article/details/89715415

https://blog.csdn.net/starter_____/article/details/82085040