强化学习课程笔记之policy-based方法

Policy-based和Value-based是RL中Model-free的两大分支，关于value-based的课程笔记，点这里(个人认为将李宏毅教授的强化学习笔记结合Sutton强化学习书籍一起学习会更好)。本篇是关于Policy-based的课程笔记。
课程笔记参考：
李宏毅笔记(github版)、叶强pdf、Morvan、刘建平博客园
论文阅读
Sutton强化学习书籍

常见的Policy-based方法：

1. REINFORCE(Vanilla-PG)
2. A2C
3. A3C
4. DDPG
5. TD3
6. Smoothie
7. SAC系列(SQL)
8. PPO系列(TRPO、DPPO)

为什么要学习policy-based，value-based缺陷在哪？

1. 
2. 对受限状态下的问题处理能力不足。在使用特征来描述状态空间中的某一个状态时，有可能因为个体观测的限制或者建模的局限，导致真实环境下本来不同的两个状态却再我们建模后拥有相同的特征描述，进而很有可能导致我们的value-based方法无法得到最优解。
3. value-based的最优策略是确定性策略，是通过最大化值函数所对应的动作产生的。但有些需要RL的最优策略确实随机策略。比如“石头剪刀布”游戏，如果你一直遵循确定性策略，那么就会被对手掌握规律，但如果输出随机性策略，那么对手就不会掌握到你的出手规律。
4. 综上所述，对于连续动作空间、状态表达受限、输出随机策略的RL任务来说，policy-based方法的优势就很明显了。

0 PG算法原理

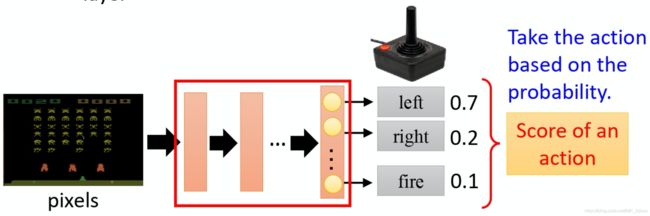
在policy-based方法中，我们有三大成分：actor（即Agent）、环境、奖励函数。value-based如Q-learning算法是一种输出值函数，然后根据最大值函数来求解动作。而policy-based是直接输出动作的，故其可以解决连续动作的RL问题。在强化学习里面，环境跟奖励函数不是你可以控制的，环境跟奖励函数是在开始学习之前，就已经事先给定的。你唯一能做的事情是调整演员里面的策略(policy)，使得演员可以得到最大的奖励。演员里面会有一个策略， 这个策略决定了演员的行为。策略就是给一个外界的输入，然后它会输出演员现在应该要执行的行为。
Note:

1. 在policy-based中，我么将策略看成一个神经网络。
2. 输入就是游戏的画面，它通常是由像素(pixels)所组成的。
3. 输出就是有哪些选项是你可以去执行的，输出层就有几个神经元，假设你现在可以做的行为有 3 个，输出层就是有 3 个神经元。每个神经元对应到一个可以采取的行为。
4. 输入一个东西后，网络就会给每一个可以采取的行为一个分数。你可以把这个分数当作是概率。演员就是看这个概率的分布，根据这个概率的分布来决定它要采取的行为。比如说 70% 会向左走，20% 向右走，10% 开火等等。概率分布不同，演员采取的行为就会不一样。

Policy-gradient算法是整个policy-based算法的基础，它的功能就是让策略网络参数$\theta$的更新朝着性能度量$J(\theta )$上升的方向移动，所以他是个梯度上升：
$$\begin{gathered} {\theta }_{t+1}={\theta }_t+\alpha {\nabla }_{{\theta }_t}J({\theta }_t) \\ {\nabla }_{{\theta }_t}J({\theta }_t)\propto \mathbb{E}[{\nabla }_{{\theta }_t}J({\theta }_t)] \end{gathered}$$
对于性能度量$J$通常会取值函数，这样也符合RL的目标——最大化期望累计奖励。根据这个特性，在一般的policy-based算法中，策略梯度上升也经常作为策略提升处理。
现在的目标就是将值函数代入上述公式的$J$中，参考Sutton强化学习的推导可得出：
$$\nabla J(\theta )=\nabla V^{\pi }(\theta )\propto \sum _s\mu (s)\sum _a\nabla {\pi }_{\theta }(a|s)Q^{\pi }(s,a)$$Note：

1. $\mu (s)$为同轨策略分布。
2. 对于连续随机变量，也可以写成$J(\theta )={\int }_{\mathcal{S}}\mu (s){\int }_{\mathcal{A}}{\pi }_{\theta }(a|s)Q^{\pi }(s,a)\mathrm{d}a\mathrm{d}s$

所以我们的PG单样本更新进一步变成：
$${\theta }_{t+1}={\theta }_t+\alpha \sum _a{\nabla }_{\theta }{\pi }_{\theta }(a|s_t)Q^{\pi }(s_t,a)$$

1 REINFORCE算法

REINFORCE算法将从PG算法的$Q$改成期望累计奖励$G$，详细推导见Sutton强化学习。李宏毅老师通过另一种方法也推出了REINFORCE算法的更新公式：
我们都知道，RL的目的就是最大化累计奖励。但是由于actor处于一个陌生环境中，她一开始并不知道会怎么走，会获得多少奖励，动作都是随机的，因此相应获得的奖励也是随机的。故我们的目标就是累计奖励的估计值，即求它的期望。将他的期望当作我们的目标。因此我们就要最大化这个期望累积奖赏。policy-based通过梯度上升的方式去达到这个目标，具体的：在某一场游戏里面，某一个回合里面，我们会得到R。我们要做的事情就是调整演员内部的参数$\theta$使得R的值越大越好。具体公式推导为：Note：

1. 这里用对数函数$\log$，是因为对数函数有更好的收敛性。

具体实现过程：Note：

1. 首先actor与环境交流，获取第一串轨迹。
2. 我们将数据带入我们推导的这个梯度式子中，然后更新$\theta$。
3. 将更新过的网络继续去采集下一串轨迹，重复步骤②③。
4. 每一串轨迹只使用一次，用完就丢掉了。

将Policy Gradient看成是神经网络的分类问题：
经典的多分类问题通过Cross-Entropy 这个Loss function来求解，而我们的policy gradient也可以看成是分类问题：
Note：

1. 每串轨迹中的每个状态------>每个图片样本（同理每串轨迹------>1个batch图片样本）；输出每个动作的概率------>每个数字类别的概率；实际采样输出的动作$a$------>每个样本的标签。
2. 这个实际的动作$a$只是我们输出的真实的动作，它并不一定是正确的动作，它不能像手写数字识别一样作为一个正确的标签来去指导神经网络朝着正确的方向去更新，所以我们需要乘以一个奖励回报$G_t$​。这个奖励回报相当于是对这个真实动作的评价：①如果$G_t$​​ 越大，未来总收益越大，那就说明当前输出的这个真实的动作就越好，这个 loss 就越需要重视。②如果$G_t$​​ 越小，那就说明做这个动作$a$并没有那么的好，loss的权重就要小一点，优化力度就小一点。从这里就可以看出，为什么叫“强化”学习！

从上面我们就可以看出policy gradient存在的4个问题！
Q1：
既然这个奖励回报是crisis，只要在同一个回合里面，在同一场游戏里面， 所有的状态跟动作的对都会使用同样的奖励项(term)进行加权，这件事情显然是不公平的，因为在同一场游戏里面 也许有些动作是好的，有些动作是不好的。 假设整场游戏的结果是好的， 并不代表这个游戏里面每一个行为都是对的。若是整场游戏结果不好， 但不代表游戏里面的所有行为都是错的。所以我们希望可以给每一个不同的动作前面都乘上不同的权重。每一个动作的不同权重， 它反映了每一个动作到底是好还是不好。因此改动的做法就是：只计算从这一个动作执行以后所得到的奖励。因为这场游戏在执行这个动作之前发生的事情是跟执行这个动作是没有关系的， 所以在执行这个动作之前得到多少奖励都不能算是这个动作的功劳。跟这个动作有关的东西， 只有在执行这个动作以后发生的所有的奖励把它加起来，才是这个动作真正的贡献。这个我们已经很熟悉了，因为之前在value-based里面，每个状态值函数的G就是从当前状态开始的，并且考虑到未来的不确定性， 还加了$\gamma$进行衰减，如下图所示：我们前面说过policy-based的目标就是求解出策略网络，通过更新网络参数$\theta$来最大化期望累计奖赏。那么如何将上述步骤融入到PyTorch的正向推理和反向传播中去呢？
其实就一句话：最小化交叉熵就是最大化对数似然。意思就是，我们现在的目标是最大化：那就等效于最小化：而后面这个式子与PyTorch中的Cross-Entropy loss function非常类似，我们只需稍微改动，就可以利用这个Loss function进行优化。
那么现在这个式子是我们一串轨迹样本的Loss，是Loss而不再是奖励。我们不妨一个一个样本考虑（把求和号去掉）：如果当前样本产生的G很大，那么其Loss也会很大，那么梯度值就会很大，经过反向传播，然后梯度下降更新参数，那么再次正向推理的时候，之前那个动作输出的概率就会得到加强提升。反之，若G很小，那么概率的提升就会很小。当G是负数时，那么梯度下降就会往反方向去，那么之前那个动作输出的概率就会下降，这就是G起到评价输出动作的作用，也就是policy gradient的核心思想。
Note:

1. 加负号的原因是为了让其看起来更像是“loss”，$PyTorch$或TF中的优化器都是梯度下降，都是最小化目标函数的，他只有min这个功能。
2. 这里有个小技巧，就是将一串轨迹开始训练的时候，将送入网络的这个G进行nomalization（即标准化），为什么这么做呢？根据Karpathy大神的博客：意思就是标准化可以抑制策略梯度算法回合间各个相同状态所对应衰减奖励之间的方差。个人认为这样有利于收敛，因为我们在做这个单样本梯度下降时，构建loss的时候，对Gt做标准化有利于将loss锁定在小范围内，防止较大的loss值造成网络参数更新过大，那么就会造成参数更新不稳定，幅度过大，当然做批处理也可以缓解这个问题。标准化处理如下：

Q2：
既然说$G_t$是评判家，那么如果某个RL任务的奖励都是大于0的，经过反向传播，那岂不是某个状态s的所有动作a的概率都会上升吗，几个动作的概率和为1这个constrain的存在会使得比如说，3个动作$a_1、a_2、a_3$，我采样到了$a_1$，使得输出$a_1$的概率上升了，那么没采样到的$a_2、a_3$就可能会下降，但是这样对a2、a3岂不是不公平吗，如果说a2是一个很好的动作，那么$a_2$的下降岂不是不合理吗？解决这个的办法就是引入baseline，引入之后：这个b是怎么工作的呢？
如果得到的总奖励大于 b 的话，就让它的概率上升。如果这个总奖励小于 b，就算它是正的，正的很小也是不好的，你就要让这一项的概率下降。 如果小于b ， 你就要让这个状态采取这个动作的概率下降。所以在实现训练的时候，你会不断地把每个G记录下来 然后你会不断地去计算 G的平均值， 你会把这个平均值，当作你的b来用。（平均值可以考虑用增量式计算来缩小存储）
R-b这一项合起来，称为优势函数$A^{\pi }(s,a)=Q^{\pi }(s,a)-V^{\pi }(s)$。它取决于s和a。在后续的Actor-Crisis里面，这个A是用叫做critic网络估计出来的。你需要有一个模型去跟环境做互动，你才知道接下来得到的奖励会有多少。A的上标是$\theta$，说明使用θ参数的网络去和环境互动，然后得到一串轨迹，各个状态计算各自的优势函数，然后去更新$\theta$。Note:

1. 1、引入baseline还有一个作用是减小方差，增强梯度更新的稳定性(类似方法还有期望、标准化、归一化、minibatch、KL散度等)
2. 优势函数第一次出现应该是在Dueling Network中，A=Q-V。
3. Baseline的减小方差可以使得收敛速度加快。(参考sutton强化学习书籍P40)

Q3：
我们的目标是设计一个最佳的策略函数π，这个π在前面一直是以符号或者网络图形展现的，具体咋设计呢？针对行为是否连续，分为Softmax策略和高斯策略：两者处理方式如下：​
离散下按概率采样动作即可，不用多说。连续下，我们通常需要知道动作的最大值action_lim，比如拉力在[-2,2]，action_lim=2，我们一般都通过tanh将输出归一在[-1,1],然后乘以action_lim输出具体动作值。PG是On-policy算法，Actor先去跟环境互动去搜集资料，搜集很多的，根据它搜集到的资料，会按照policy gradient的式子去更新 policy 的参数。所以 policy gradient 是一个on-policy的算法。

Q4：
​
这是REINFORCEMENT的核心公式，我么已经知道，这是一种on-policy算法，这没有问题，因为采集信息和更新都是一个策略。那么这种on-policy就有个问题，从公式中我们看出，他必须等采集了完整一条轨迹之后，再更新参数，这个过程耗时不说，更要命的是更新后，刚才那条轨迹就不能在用了，是disposable的，根源在下标$\tau \sim p_{\theta }(\tau )$。​
也就是说花了很久去采样的东西，只能用一次，就要被迫丢掉，效率低且浪费严重。要知道实际上我们都是用nn去做PG的，他有个学习率，学习率的存在使得一份数据光一次训练是无法直接收敛的，原理上每多用一次，就会更接近目标。所以如果让一个策略去采集信息，另一个策略就来训练，那么他采他的，我训练我的，我可以抽空把同一条轨迹多训练几遍，那么是很nice，此外你在采集的时候，我训练，不耽误功夫，效率也高。这里的典型代表就是REINFORCE和PPO。

​REINFORCE算法流程：
常见2种REINFORCE算法：可见我们上述所研究的policy gradient其实是结合MC的回合更新的思想，将他具体化一个算法就是-----REINFORCE算法，也是最简单的policy gradient算法。
伪代码如下：
Note：

1. 根据我们之前所说，一个步伐的可以看成一个样本，上面显然是单样本更新，类似于SGD，我们其实有更快的方法，参考小批量梯度下降，就是将一串轨迹整体做梯度下降。

REINFORCE算法的缺陷：

1. 效率低，因为采用回合更新。
2. 方差大，采用G作为目标，而之前在value-based中说过，G作为目标，其不稳定，同一个状态的同一个动作，其G=100，有时候G=-10。故可以对G求期望，因为均值相对会稳定些，根据值函数的定义，可以采用Q来代替。
3. 解决办法：结合①②，最佳方案就是就是将MC取代为TD。采用actor-critic算法，它融合了TD的思想，不采用回合更新，而是单步更新，故效率高，此外，TD算法方差小，更加稳定。

REINFORCE实战，点这里

2 Vanilla Policy Gradient

你可能经常在论文中看到Vanilla policy gradient(REINFORCE)或者Vanilla policy gradient/REINFORCE这样的写法，那是因为VPG和REINFORCE几乎是完全一样，只不过有一丢丢的区别，你可以近似理解为这两个只是名字不同。
直接上VPG伪代码：
Note：

1. 红圈红线部分是VPG区别于REINFORCE的地方，在REINFORCE算法中，我们利用蒙特卡洛方法去计算一条轨迹$\tau$的累计奖励$R$，然后把这个奖励放到梯度上升的式子里去做优化，从而迭代更新$\theta$；而在VPG里面，他把$R$拿过来去使用最小二乘损失，用mini-batch梯度下降优化出一个$V$函数。因此本质上VPG和REINFORCE是相同的算法，并没有很大的区别。
2. 关于VPG有2个比较热门的开源库，分别是OpenAI Spinning Up以及rllab。
3. 有关VPG进一步解读或者公式推导，也可以参考另一位博主的(点这里)，因为和REINFORCE类似，我就不详细介绍VPG了。

3 A2C算法

A2C：Advantage Actor Critic算法。
policy gradient结合MC的思想就是REFORCEMENT算法，采用回合更新策略网络。
REINFORCEMENT缺陷就是：
①：效率低。
②：直接用累计奖励做critic，其方差较大，收敛过程不稳定，回合间相同状态的累计奖励之间可以通过nomalization来缓解不稳定性。
针对这两点，Actor critic算法就诞生了，其用policy gradient结合TD的思想，采用步进更新策略网络。

3.1 算法简介

根据critic的不同，大致可将Actor critic分为A2C(Advantage actor critic)、A3C(Asynchronous advantage actor critic)、QAC(Q Advantage actor critic)三类。
如上图所示，在做policy gradient的时候，就算以衰减G为critic，其方差大问题还是存在，造成了收敛的不稳定性，因此我们需要将这个critic换成其期望的形式，即E(G),这样可以抑制方差大带来的不稳定。
看到G，首先想到的就是value-based方法中的Q值函数，没错这里我们就是用Q值来取代G，至于后面的b，即baseline我们可以用V值函数来替代。
这样的话，优势函数Advantage function就变成了Q-V，而V是Q的期望值，故Q-V也是有正负的，这也符合我们设计baseline的初衷。
但是这样也存在一个小问题，除了策略网络以外，你还需要设计2个网络：即Q网络和V网络，为了简化成一个网络，可以对Q做个变式：回忆一下贝尔曼等式：这里可以进一步简化，根据期望公式，可转换成：虽然都说贝尔曼等式在有模型下才能用，但是上述这个等式在推导过程中可以约去转移概率P，故可以成立。
因此我们的优势函数就变成了：这样我们设计一个网络就可以了，这其实就是TD error的值函数表达式。整个AC算法结构：
最后你会发现，其实就是用TD error代替了G，其实V也可以充当TD目标值。只不过我们当初选择Q是因为，一是Q能选择动作而V不能；第二是因为当初用V做的时候，经过预测和控制之后，V仍需要转成Q，有了贝尔曼公式就很方便，然后用贪心策略从Q中选出了动作，那么model-free没有贝尔曼公式中的转移概率P，故为了省去这一步，我们直接选择了Q。但是现在动作有policy网络输出，故我们可以不用Q了。其实Q和V从定义就可以看出没啥大差别，就相差了个动作而已，都表达了未来价值的期望值。
上图是网络结构图，和Dueling网络一样之后，由共享网络和子网络组成，子网络分别为策略网络和V估计网络。

3.2 伪代码

​
A2C算法流程：以下伪代码是on-policy版的A2C，因为行为策略和目标策略均为一个策略，A2C没有官方的伪代码，但是从A3C的代码中看出A2C是如下所示，现在网上实现的A2C都是这种形式。
需要注意的是，不管要不要加IS，A2C都是on-policy算法，因为更新的关键在于，Critci只是辅助作用。
正因为只有一个策略（on-policy），因此Critic估计的V值不需要再加IS修正，即伪代码第7行的中不需要加IS修正因子。
虽然A2C在实现上是TD error的形式，但实现上这种需要估计Q、V网络的做法是不可取的，因为如果估计不准确的话，会造成双倍的风险。
其实就是根据定义，看策略网络有几种策略输出，AC需要判断Actor和Critic各自是否off-policy。但两者是联合的，也就是说，一个是on-policy，另一个一定不是off-policy。一般以判断Actor为主，有2个策略的，则是off-policy的AC算法，如DDPG：确定性策略和带噪声的确定性策略。on-policy的AC典型的就是上面这个A2C，因为Actor只输出一个策略。

下面这个Critic基于Sarsa的on-policy算法，我觉得也行，根据QAC对应改编的。Note：

1. 从实战效果来看，第一个A2C效果略好于第二个，存在少数的收敛，第二种几乎不收敛。

另一种直接利用Q的是QAC，即Critic是Q值，这是一种on-policy AC算法，因为其Critic是Sarsa，故如下所示：

​

3.3 小结

1. 除了使用优势函数作为critic以外，还可以使用其它的，比如：
2. 基本版的Actor-Critic算法虽然思路很好，但是由于难收敛的原因，还需要做改进。Actor-Critic 涉及到了两个神经网络, 而且每次都是在连续状态中更新参数, 每次参数更新前后都存在相关性, 导致神经网络只能片面的看待问题, 甚至导致神经网络学不到东西。Google DeepMind 为了解决这个问题, 修改了 Actor Critic 的算法,
   目前改进的比较好的有两个经典算法，一个是DDPG算法，使用了双Actor神经网络和双Critic神经网络的方法来改善收敛性。这个方法我们在从DQN到Nature DQN的过程中已经用过一次了。另一个是A3C算法，使用了多线程的方式，一个主线程负责更新Actor和Critic的参数，多个辅线程负责分别和环境交互，得到梯度更新值，汇总更新主线程的参数。而所有的辅线程会定期从主线程更新网络参数。这些辅线程起到了类似DQN中经验回放的作用，但是效果更好。

A2C实战部分，点这里

4 A3C算法

A3C论文笔记，点这里

4.1 A3C简介

A3C：即Asynchronous Adavantage Actor-Critic

针对A2C难以收敛原因之一的输入连续性问题，就出了2大分支，一个是DDPG，采用Experience Reply。另一个是A3C，采用多线程并行更新网络参数的方式。体现2种不同的解决问题的思想。A3C是针对多块CPU上的，GA3C是针对多块GPU上的，GA3C相对A3C速度更快，且节省内存。

下图是A3C的示意图：
Note：

1. ​Google DeepMind提出的一种解决 Actor-Critic 不收敛问题的算法. 它会创建多个并行的环境, 让多个拥有副结构的 agent 同时在这些并行环境上更新主结构中的参数. 并行中的 agent 们互不干扰, 而主结构的参数更新受到子结构提交更新的不连续性干扰, 所以更新的相关性被降低, 收敛性提高。
2. 主Agent汇聚了所有人的经验，多个子Agnet并行更新主Agent的双网络参数，使得这种算法不需要像DQN、DDPG那样有经验回访池。
3. A3C的核心思路，它利用多线程的方法，同时在多个线程里面分别和环境进行交互学习，每个线程都把学习的成果汇总起来，整理保存在一个公共的地方。并且，定期从公共的地方把大家的齐心学习的成果拿回来，指导自己和环境后面的学习交互。
4. 通过这种方法，A3C避免了经验回放相关性过强的问题，同时做到了异步并发的学习模型。线程之间互不干扰，独立运行。
5. 每个线程和环境交互到一定量的数据后，就计算在自己线程里的神经网络损失函数的梯度，但是这些梯度却并不更新自己线程里的神经网络，而是去更新公共的神经网络。也就是n个线程会独立的使用累积的梯度分别更新公共部分的神经网络模型参数。每隔一段时间，线程会将自己的神经网络的参数更新为公共神经网络的参数，进而指导后面的环境交互。
6. 公共部分的网络模型就是我们要学习的模型，而线程里的网络模型主要是用于和环境交互使用的。
7. 每一个 actor 跟环境做互动，互动完之后，你就会计算出梯度。计算出梯度以后，你要拿梯度去更新你的参数。你就计算一下你的梯度，然后用你的梯度去更新 global network 的参数。就是这个 worker 算出梯度以后，就把梯度传回给中央的控制中心，然后中央的控制中心就会拿这个梯度去更新原来的参数。
8. 所有的 actor 都是平行跑的，每一个 actor 就是各做各的，不管彼此。所以每个人都是去要了一个参数以后，做完就把参数传回去。所以当第一个worker做完想要把参数传回去的时候，本来它要的参数是​，等它要把梯度传回去的时候。可能别人已经把原来的参数覆盖掉，变成了。但是没有关系，它一样会把这个梯度就覆盖过去就是了，这个就是 A3C。
   ​

4.2 伪代码

4.3 小结

A3C解决了Actor-Critic难以收敛的问题，同时更重要的是，提供了一种通用的异步的并发的强化学习框架，也就是说，这个并发框架不光可以用于A3C，还可以用于其他的强化学习算法。这是A3C最大的贡献。目前，已经有基于GPU的A3C框架，这样A3C的框架训练速度就更快了。

5 DDPG系列算法

5.1 DPG算法

DPG主要的四大贡献：

①：确定性策略a=(s),而非之前的随机策略，e.g. 高斯策略和softmax策略
②：调整策略参数θ朝着值函数Q梯度上升的方向。
③：确定性策略梯度的performance objective只对状态积分，相比于随机性策略，对动作的积分空间大大减少，意味着无需对动作进行采样了，大大提高了效率。
④：Actor使用确定性策略，其对动作不积分不采样，不需要IS修正因子。

​关于DPG论文笔记，点这里

5.2 DDPG算法

DDPG的论文主要是介绍DQN + DPG的结合，然后给出一套伪代码以及实验，全文比较简单，读者可以自行去简要看下。

5.2.1 DDPG简介

DPG：引入点，随机策略对于高维动作空间不适用，即上述DPG的第②个贡献点。

5.2.2 DDPG框架结构

确定性指的是策略网络输出的动作是确定性的，当然后期为了在这个确定性的基础上，会有一定的上下浮动，即噪声，用于增强一定的探索能力。在之前的softmax或者高斯策略中，一个用于离散动作，一个用于连续动作，其动作实在这两个策略的输出分布中采样获取，是随机性策略。而Determinister就好像说：“softmax兄弟，既然你最终都是要输出一个动作的，为啥要这么犹豫去随机选取呢，直接输出一个确定的动作不就好啦”。

DDPG核心思想：如上图框架结构所示，将Nature DQN的思想与policy gradient结合在一起，构建四个网络：策略网络、策略目标网络、Q估计网络、Q目标网络。

5.2.3 DDPG解析

DDPG由DQN和DPG组成，DQN（指Nature DQN）采用了Experience Reply以及Target Network两项关键技术，分别解决了RL中样本输入连续、相关性强，导致无法通过nn训练的问题以及TD目标值和Q估计值难以靠近的不收敛问题。
DDPG是DQN的扩展版本，专门用于解决DQN解决不了的连续动作空间问题。其两大网络Actor和Critic网络（就是上述的DQN）都采用了Target Network技术，以及用Experience Reply来打破输入样本连续性问题，以便更好地去训练网络。
因此DDPG由策略网络、策略目标网络、Q估计网络、Q目标网络四大网络组成。具体网络结构如下：

1. Critic网络：输出为1个神经元Q(s,a)，是一个标量，离散动作常用另一种值函数近似器是输入为状态，输出为各个动作的Q值。
2. Actor网络：输出个数为动作的特征维数，每个维度下都是连续的值，比如拉力[-2,2]。是一个向量。当然也可以采用CNN、RNN等网络结构，这里只是最简单的入门结构。

Note：

1. ​经验池里的经验是怎么来的？在状态s由策略网络在一定噪声基础上输出确定性动作a（以前DQN中是由-greedy策略输出的随机性动作），与环境交流，输出s’,r，以及done信息，将这一个Trans信息存入池中。
2. Q网络的输入是什么？从经验池中随机打乱抽取的batch份trans，取出每一份的s，a作为Q估计网络的输入。
3. 策略网络的输入是什么？从经验池中随机打乱抽取的batch份trans，取出每一份的s作为策略网络的输入。
4. TD error由哪几部分组成？TD目标值中Q是Target Q网络，其输入s’为来自于经验池的batch份数据，a’来自于Target 策略网络。
5. 为何设置Target网络？和为啥设置Target Q网络一样，a’不能直接来自于策略网络，因为TD目标值的输出是作为标签存在的，为了避免难收敛，我们让其处于一定时间内不改变或者微改变，而a‘决定了TD目标值的大小，a’若来自于策略网络，策略网络在训练后是要和Q网络一样及时更新的，一旦及时更新后，a’的值势必会改变，意味着标签变动了，那么之前的那次Q值更新就变得毫无意义了，即收敛不稳定。
6. 策略网络是怎么优化的？策略网络参数调整是沿着Q值梯度上升的方向，这是DPG的第一大贡献。这里的Q值为Q估计网络，输入为经验池中抽取的batch份的s，以及${\mu }_{\theta }(s)$,与Critic更新不同，Actor网络的更新是不涉及2个Target网络的。此外，由于PyTorch中网络参数得更新是基于Mnimise的，即梯度下降，故performance前还要加个负号，然后做backforward。
7. 4个网络的参数如何更新？初始化的时候，采用硬更新，即主网络参数完全复制给Target网络。其余时候，2个Target网络微更新，或者说软更新，就是更新一点点，具体见伪代码。2个主网络采用步进更新，每一个step都要更新。
8. 既然是off-policy算法，那么其两个策略是咋样的？行为策略是策略网络输出的基础上设置一定的噪声（常见Ornstein-Uhlenbeck、高斯噪声）来实现一定程度的探索。在之前DQN的离散动作空间下，选择状态s’下最大Q值对应的动作，而由于是连续动作空间，故不能这样做，因此，为了挑选状态s’下最大的Q值，Sutton在DPG论文中提出另一种新的思想，即DPG的第一大贡献，根据目标策略其实类似于之前的贪婪策略，它换了一种形式，通过策略网络的训练使得Q值不断变大，那么在状态s’下，这样的Q值选出来的确定性动作a’才能使Q值最大化。此外，Sutton在DPG中还给出更加formal的证明方式。
9. DDPG噪声的选择有2种，一种是OU噪声：​其中$\mu 、\theta 、\varphi$为需要调节的超参数，超参数的调节也成为了DDPG被人诟病的地方。一维高斯噪声就直接用PyTorch的内置函数输出即可。

5.2.4 DDPG伪代码

Note：

1. ​①：DDPG仿照DQN，主网络参数到Target网络参数有2种赋值方式，一种是软更新，或者说微更新，即每次只更新一点点（相当于DQN中的过一阵子再更新），另一种是硬更新，即算法刚开始的时候，保持主网络和Target网络参数完全一致。
2. ②：也是仿照DQN，DDPG设置了Experience Reply，勇于打破数据相关性，便于nn学到东西。
3. ③：和DQN不用，DQN中我们的行为策略采用-greedy策略，而DDPG采用策略网络，因此是在确定性策略基础上增加了O-U噪声（或者李宏毅说的高斯噪声也不错）来增加探索能力。DQN的目标策略是贪心策略，而DDQN也是“贪心策略”，但换了一种思想，参照Sutton DPG论文，他的方式是调整网络参数朝着Q值梯度上升的方向。那么当我们在计算TD目标值的时候，输入s’,那么此时用策略目标网络选择输出的动作a’一定能弄出一个比较大的Q值来，他以这种方式来取代贪心策略的max用法。根本原因还是在于连续动作空间下，你用max策略是无法选出最大Q值对应的那个动作action的，即globally maximize。
4. ④：在测试的时候，回忆下DQN或者Q-learning，我么是直接采用贪心策略的，去掉了-greedy中的探索性，这是我们的目标策略，而且必须是个确定性策略。那么在DDPG中，我们的目标策略就是我们网络直接输出的确定性策略，经过策略网络参数的训练，此时的策略网络能根据输出状态s，输出具有很大Q值得动作a，这其实就几乎等价于贪心策略的效果啦！具体措施就是拿掉噪声的加成，直接输出网络的结果。
5. ⑤：注意绿色框，在actor网络的更新中，构建Q值并使参数沿着Q值梯度上升的方向更新，这个构建Q值的动作a并不是来自于经验回放池，而是来自于经验回访池的s经过actor网络输出的实时动作a。参考Silver论文中推导出的公式：，这也就是上述伪代码中的Actor网络更新部分。

总结：DDPG中。Critic给Actor提供准确的Q值，从而更新参数θ。Actor给Critic提供行为策略和目标策略（max化Q），两者相辅相成，共同进步，最终Critic能估计出Q真实值，而Actor能输出最优策略。

DDPG实战，点这里

6 TD3算法

TD3算法是DDPG的进阶版，训练稳定性更强，且缓解了AC算法Critic过估计问题。
TD3理论部分：TD3论文笔记
TD3实战部分：TD3实战

7 Smoothie算法

Smoothie算法引入了一种新的$Q$——平滑$Q$，其策略网络是多维高斯分布，要训练三个网络$\mu 、\Sigma 、\omega$，分别是高斯分布的均值网络、协方差网络以及Critic网络。总的来说其结构还是基于DDPG。
Smoothie论文笔记，点这里

8 SAC系列算法

和Smoothie算法一样，SAC系列算法引入了新的$Q$——$Q_{soft}$，而且其改变了RL的目标函数为——最大化含熵目标，因此需要重新设计软贝尔曼等式。

8.1 SQL算法

SQL论文笔记，点这里

8.2 SAC算法

SAC论文笔记，点这里
SAC提升版算法笔记，点这里

9 PPO系列算法

PPO系列算法旨在设计一种策略单调不减的算法，是为了解决PG中学习率大小的算法。这个系列算法的不直接优化传统的RL目标$\eta$，而是去优化$\eta$的近似替代函数。

9.1 TRPO算法

TRPO论文笔记，点这里

9.2 PPO算法

PPO比TRPO更加实用，对于TRPO我们只要掌握其理论即可，实战还得靠PPO，因此我们详细介绍PPO
PPO论文笔记，点这里
Note：

1. PPO论文的导出是直接来源于TRPO，这里我们采用李宏毅老师的推导，用另一个角度来看PPO。

PPO，即Proximal Policy Optimization（近端策略优化），根据OpenAI的官博，PPO已经成为他们在RL上的默认算法。在OpenAI提出TRPO(Trust Region Policy Optimization)后，DeepMind和OpenAI先后发布了DPPO(Distributed PPO)和PPO算法。PPO算法是一种On-policy算法，即和环境交流的策略与目标（训练用的）策略不是一个策略。

PPO = Policy-Gradient + Importance Sampling + KL散度，意思就是说PPO是一种在on-policy PG算法上使用IS技术，并用KL散度消除因IS新旧分布相差过大导致方差较大缺陷的一种算法。

因此，PPO算法的推出需要历经2个步骤：

1. 引入IS因子，提高采样效率。
2. 引入KL散度，保证IS的有效性以及提高算法稳定性。

9.2.1 IS化PG

这里我们使用对PG改进版本的PG算法，即用优势函数A代替G：
通过重要性采样（关于IS，可查看我的另一篇博客），我们可以将上面这个on-policy改成：Note：

1. 这里的$\frac{p_{\theta }}{p_{{\theta }^{\prime }}}$是新旧策略的比值。

进一步转换：这里第二步到第三步是直接忽略掉了，不是啥数学原因，纯粹为了方便计算。此外，看到什么状态往往跟你会采取什么样的动作是没有太大的关系的。比如说你玩不同的 Atari 的游戏，其实你看到的游戏画面都是差不多的，所以也许不同的策略对状态的概率是差不多的，比值为1。
因此我们可以通过求导的链式法则和$\nabla f(x)=f(x)\cdot \nabla \log f(x)$,推导出目标函数：接下来，我们将这个新旧策略的比值看成是新策略${\theta }_{new}$和旧策略(当前策略)${\theta }_{old}$的比值。

9.2.2 引入KL散度

IS采样的缺陷在于2个新旧分布不能相差太大，否则会导致方差相差很大（即稳定性降低），从而使得两者的样本均值不一样。PPO为了解决这个问题，使得2个分布相差不大，就引入了一个约束条件，这个约束就是KL散度，用来衡量和有多相似。
KL散度就相当于L2正则化项一样，像约束着$\omega$尽量小一样约束${\theta }_{old}$和${\theta }_{new}$尽量相似。
PPO的前身是TRPO，两者不同在于KL的位置，TRPO将constrain放在约束条件上，PPO略微简单，像加L2正则化一样将约束加到了performance objective一起优化。具体如下图所示：​
引入KL后，上图就是PPO算法！KL的引入使得方差不会相差很大，也就是保证了算法的稳定性。
Note：

1. 我们让新旧两个分布尽量相似目的是让他们在同一个状态下，输出的动作值尽量相似，而不是让2个参数和的2-范数有多小（即距离小），这就是KL在做的事，它描述得是行为距离，而不是参数距离。
2. $KL$散度又叫相对熵。
   ​

9.2.3 PPO的两大变体

9.2.3.1 PPO-Penalty

PPO设定了可自动调节的$KL$因子$\beta$：

​
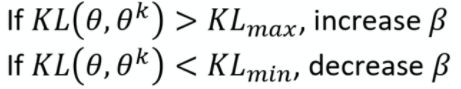
我们一开始会自己设定一个$K{L}_{max}、K{L}_{min}$，如果参数更新完后，我们的KL项比我们设定的值大，那么就增加，否则就减小。这个就叫做Adaptive KL Penalty。

9.2.3.2 PPO-Clip

这个算法比上面这个算法更容易实现，因为他用clip函数巧妙避开了KL的计算。
顾名思义，PPO-Clip中涉及到了Clip函数，就是如果x大于max值，则输出max，x小于min值，输出为min值，否则输出为x。
Clip版本目标函数：

那么它是如何使得2个动作分布相差不大的呢？

A是优势函数，A>0说明我们需要加强这个动作，A<0，代表这个动作相对不太好，我们要抑制这个动作的概率。

如上面2张图所示，绿色线是蓝色线是，红色线就是他们当中的最小值，也就是我们直接去利用的数，这里简记为Target。
分析：假设$ϵ=0.2$

1. 当A>0时，我们要加强这个动作，因此我们的更新会使得$p_{\theta }$变大，如果没有造成$\frac{p_{\theta }}{p_{{\theta }^k}}$大于1.2，那么就让$p_{\theta }$提升吧。如果大于1.2的话，我们的参数更新就停留在Target=1.2这个值了，再也不会往上上升。
2. 当A<0时，我们要抑制这个动作，因此我们的更新会使得$p_{\theta }$变小，如果没有造成$\frac{p_{\theta }}{p_{{\theta }^k}}$小于0.8，那么就让$p_{\theta }$下降吧。如果小于0.8的话，我们的参数更新就停留在Target=0.8这个值了，再也不会往下下降。

总结：
PPO是一个实现起来较容易且在连续动作空间环境下表现效果不错的算法，是一个很不错的baseline。

​​​​