1. 前言
分形几何是几何数学中的一个分支,也称大自然几何学,由著名数学家本华曼德勃罗( 法语:BenoitB.Mandelbrot)在 1975 年构思和发展出来的一种新的几何学。
分形几何是对大自然中微观与宏观和谐统一之美的发现,分形几何最大的特点:
- 整体与局部的相似性: 一个完整的图形是由诸多相似的微图形组成,而整体图形又是微图形的放大。
局部是整体的缩影,整体是局部的放大。
- 具有自我叠加性: 整体图形是由微图形不断重复叠加构成,且具有无限叠加能力。
什么是分形算法?
所谓分形算法就是使用计算机程序模拟出大自然界的分形几何图案,是分形几何数学与计算机科学相融合的艺术。
由于分形图形相似性的特点,分形算法多采用递归实现。
2. 分形算法
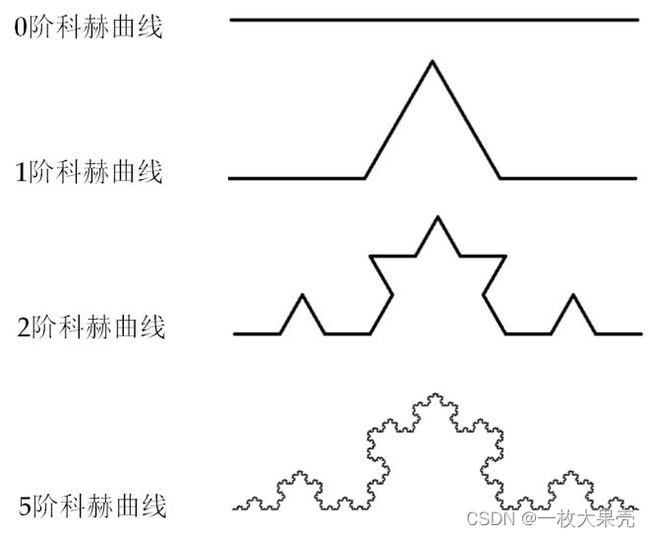
2.1 科赫雪花
科赫雪花是由瑞典数学家科赫在 1904 年提出的一种不规则几何图形,也称为雪花曲线。
分形图形的特点是整体几何图形是由一个微图形结构自我复制、反复叠加形成,且最终形成的整体图案和微图形结构一样。在编写分形算法时,需要先理解微图案的生成过程。
科赫雪花的微图案生成过程:
- 先画一条直线。科赫雪花本质就由一条直线演化而成。
- 三等分画好的直线。
- 取中间线段,然后用夹角为 60° 的两条等长线段替代。
- 可在每一条线段上都采用如上方式进行迭代操作,便会构造出多层次的科赫雪花。
科赫微图形算法实现:
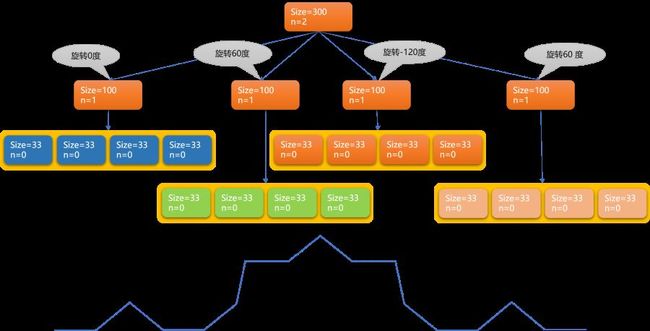
使用 Python 自带小海龟模块绘制,科赫雪花递归算法的出口的是画直线。
import turtle
'''
size:直线的长度
level: 科赫雪花的层次
'''
def koch(size, level):
if n == 1:
turtle.fd(size)
else:
for i in [0, 60, -120, 60]:
turtle.left(i)
# 旋转后,再绘制
koch(size // 3, level - 1)
参数说明:
- size: 要绘制的直线长度。
- level: 科赫雪花的层次。
0 阶和 1 阶 科赫雪花递归流程:
import turtle
turtle.speed(100)
def ke_line(line_, n):
if n == 0:
turtle.fd(line_)
else:
line_len = line_ // 3
for i in [0, 60, -120, 60]:
turtle.left(i)
ke_line(line_len, n - 1)
# 原始直线长度
line = 300
# 移动小海龟到画布左下角
turtle.penup()
turtle.goto(-150, -150)
turtle.pendown()
# 1 阶科赫雪花
di_gui_deep = 1
ke_line(line, di_gui_deep)
turtle.done()
2 阶科赫雪花:
可以多画几个科赫雪花,布满整个圆周。
import turtle
turtle.speed(100)
def ke_line(line_, n):
if n == 0:
turtle.fd(line_)
else:
line_len = line_ // 3
for i in [0, 60, -120, 60]:
turtle.left(i)
ke_line(line_len, n - 1)
# 原始线长度
line = 300
# 移动小海龟画布左下角
turtle.penup()
turtle.goto(-150, -150)
turtle.pendown()
# 几阶科赫雪花
di_gui_deep = int(input("请输入科赫雪花的阶数:"))
while True:
# 当多少科赫雪花围绕成一个圆周时,就构成一个完整的雪花造型
count = int(input("需要几个科赫雪花:"))
if 360 % count != 0:
print("请输入 360 的倍数")
else:
break
for i in range(count):
ke_line(line, di_gui_deep)
turtle.left(360 // count)
turtle.done()
4 个 3 阶科赫雪花: 每画完一个后旋转 90 度,然后再绘制另一个。
6 个 3 阶科赫雪花: 每画完一个后,旋转 60 度再画另一个。
科赫雪花的绘制并不难,本质就是画直线、旋转、再画直线……
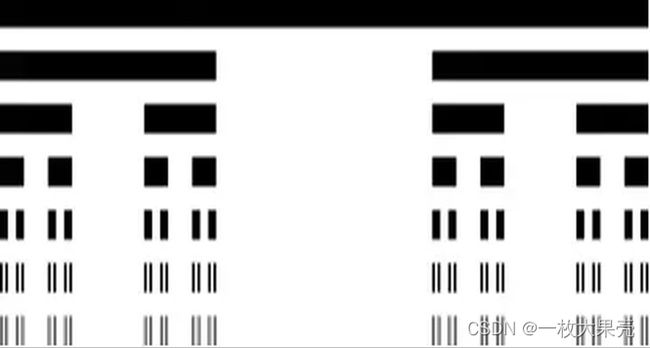
2.2 康托三分集
由德国数学家格奥尔格·康托尔在1883年引入,是位于一条线段上的一些点的集合。最常见的构造是康托尔三分点集,由去掉一条线段的中间三分之一得出。
构造过程:
- 绘制一条给定长度的直线段,将它三等分,去掉中间一段,留下两段。
- 再将剩下的两段再分别三等分,同样各去掉中间一段,剩下更短的四段……
- 将这样的操作一直继续下去,直至无穷,由于在不断分割舍弃过程中,所形成的线段数目越来越多,长度越来越小,在极限的情况下,得到一个离散的点集,称为康托尔点集。
编码实现: 使用递归实现。
import turtle
''''
(sx,sy)线段的开始位置
(ex,ey)线段的结束位置
'''
turtle.speed(100)
turtle.pensize(2)
def draw_kt(sx, sy, ex, ey):
turtle.penup()
# 小海龟移动开始位置
turtle.goto(sx, sy)
turtle.pendown()
# # 小海龟移动结束位置
turtle.goto(ex, ey)
# 起始点与结束点之间的距离
length = ex - sx
# 如果直线长线大于 5 则继续画下去
if length > 5:
# 左边线段的开始 x 坐标
left_sx = sx
# y 坐标向下移动 30
left_sy = sy - 50
# 左边线段的结束坐标
left_ex = sx + length / 3
left_ey = left_sy
# 右边线段的开始坐标
right_sx = ex - length / 3
right_sy = ey - 50
# 右边线段的结束坐标
right_ex = ex
right_ey = right_sy
draw_kt(left_sx, left_sy, left_ex, left_ey)
draw_kt(right_sx, right_sy, right_ex, right_ey)
draw_kt(-300, 200, 300, 200)
turtle.done()
康托三分集的递归算法很直观。
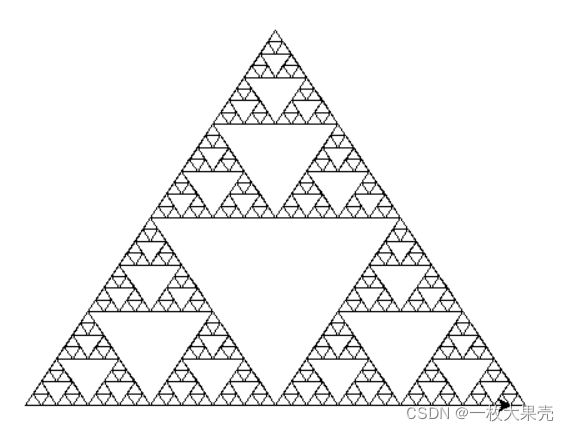
2.3 谢尔宾斯基三角形
谢尔宾斯基三角形(英语:Sierpinski triangle)由波兰数学家谢尔宾斯基在1915年提出。
构造过程:
- 取一个实心的三角形(最好是等边三角形)。
- 沿三边中点的连线,将它分成四个小三角形。
- 去掉中间的那一个小三角形。
- 对其余三个小三角形重复上述过程直到条件不成立。
编码实现: 谢尔宾斯基三角形就是不停的画三角形,在编码之前约定三角形点之间的关系以及绘制方向如下图所示。
import turtle
import math
turtle.speed(100)
'''
通过连接 3 个点的方式绘制三角形
pos是元组的元组((x1,y1),(x2,y2),(x3,y3))
def draw_triangle(pos):
turtle.penup()
# 移到第一个点
turtle.goto(pos[0])
turtle.pendown()
# 连接 3 个点
for i in [1, 2, 0]:
turtle.goto(pos[i])
# 计算三角形任意两边的中点坐标
def get_mid(p1, p2):
return (p1[0] + p2[0]) / 2, (p1[1] + p2[1]) / 2
绘制 谢尔宾斯基三角形
def sierpinski_triangle(*pos):
# 用给定的点绘制三角形
draw_triangle(pos)
p1, p2, p3 = pos
# 计算三角形的边长
side = math.fabs((p3[0] - p1[0]) / 2)
# 如果边长满足条件,继续绘制其它三角形
if side > 10:
# p1和p2线段 的中心点
p1_p2_center_x, p1_p2_center_y = get_mid(p1, p2)
# p2和p3线段 的中心点
p2_p3_center_x, p2_p3_center_y = get_mid(p2, p3)
# p1和p3线段 的中心点
p1_p3_center_x, p1_p3_center_y = get_mid(p1, p3)
# 绘制左下角三角形
sierpinski_triangle(p1, (p1_p2_center_x, p1_p2_center_y), (p1_p3_center_x, p1_p3_center_y))
# 绘制上边三角形
sierpinski_triangle((p1_p2_center_x, p1_p2_center_y), p2, (p2_p3_center_x, p2_p3_center_y))
# 绘制右下角三角形
sierpinski_triangle((p1_p3_center_x, p1_p3_center_y), (p2_p3_center_x, p2_p3_center_y), p3)
# 第一个点指左边点,第二点指上面的点,第三个指右边的点。
sierpinski_triangle((-200, -100), (0, 200), (200, -100))
turtle.done()
代码执行之后的结果:
用随机的方法(Chaos Game),绘制谢尔宾斯基三角形:
构造过程:
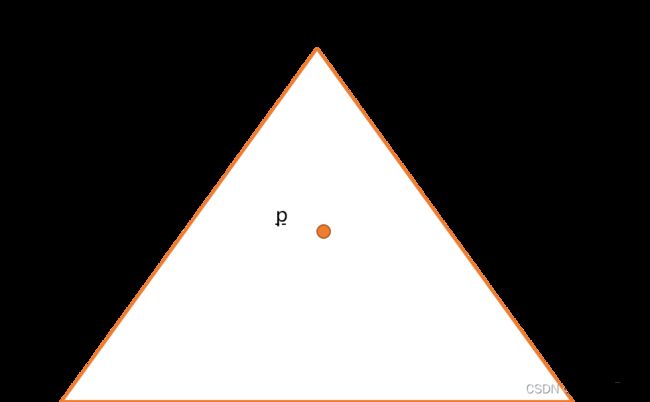
任意取平面上三点 A,B,C,组成一个三角形。
在三角形 ABC 内任意取一点 P,并画出该点。
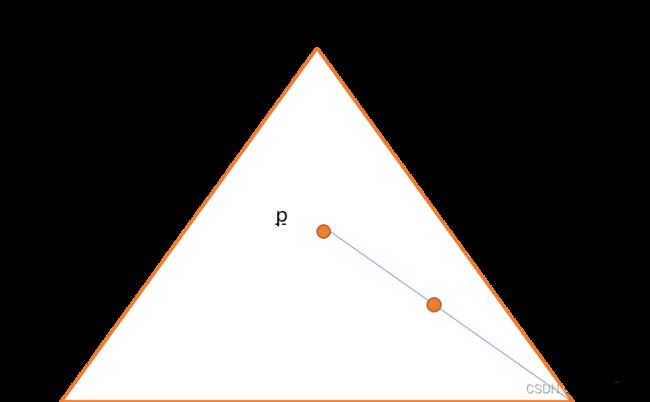
找出 P 和三角形其中一个顶点的中点,并画出来。
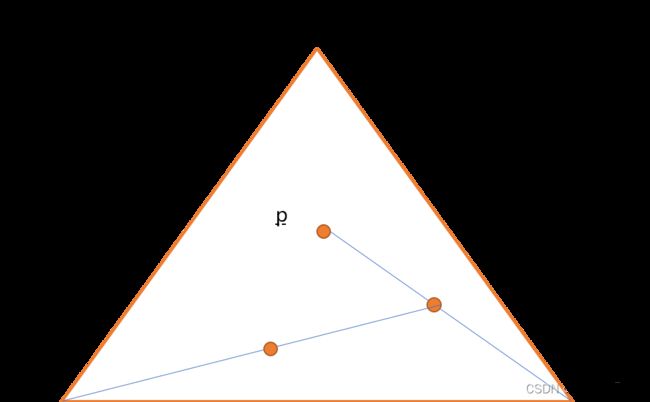
把刚才找出来的中心点和三角形的任一顶点相连接,同样取其中点,并画出来。
重复上述流程,不停的获取中心点。
注意,是画点,上面的线段是为了直观理解中心点位置。
编码实现:
import turtle
import random
turtle.speed(100)
turtle.bgcolor('black')
colors = ['red', 'green', 'blue', 'orange', 'yellow']
# 画等边三角形
def draw_triangle(pos):
turtle.penup()
turtle.goto(pos[0])
turtle.pendown()
for i in [1, 2, 0]:
turtle.goto(pos[i])
def sierpinski_triangle(*pos):
# 画三角形
draw_triangle(pos)
p1, p2, p3 = pos
# 在三角形中任取一点
ran_x, ran_y = (p1[0] + p3[0]) / 2, (p2[1] + p3[1]) / 2
for i in range(10000):
# 画点
turtle.penup()
turtle.goto(ran_x, ran_y)
turtle.pendown()
turtle.dot(3, colors[i % 5])
# 随机选择 3 个顶点的一个顶点
ran_i = random.randint(0, 2)
ding_p = pos[ran_i]
# 计算任意点和顶点的中心点
ran_x, ran_y = (ran_x + ding_p[0]) / 2, (ran_y + ding_p[1]) / 2
sierpinski_triangle((-200, -100), (0, 200), (200, -100))
turtle.done()
随机法是一个神奇的存在,当点数量很少时,看不出到底在画什么。当点的数量增加后,如成千上万后,会看到谢尔宾斯基三角形跃然于画布上,不得不佩服数学家们天才般的大脑。
下图是点数量为 10000 时的谢尔宾斯基三角形,是不是很震撼。
2.4 分形树
绘制分形树对于递归调用过程的理解有很大的帮助,其实前面所聊到的递归算法都是树形递进。分形树能很形象的描述树形递归的过程。
分形树的算法实现:
import turtle
def draw_tree(size):
if size >= 20:
turtle.forward(size) # 1
# 画右边树
turtle.right(20)
draw_tree(size - 40) # 2
# 画左边树
turtle.left(40)
draw_tree(size - 40)
# 后退
turtle.right(20)
turtle.backward(size)
turtle.left(90)
draw_tree(80)
turtle.done()
为了理解分形树的递归过程,如上代码可以先仅画一个树干两个树丫。
下面以图示方式显示左右两边的树丫绘制过程。
3. 总结
分形几何是大自然对数学的馈赠,当然这离不开数学家们的发现与研究,通过计算机科学对分形几何的模拟,可以以可视化的方式更直观地研究分形几何学。这也是计算机科学对于各学科的巨大贡献。
到此这篇关于Python 分形算法代码详解的文章就介绍到这了,更多相关Python 分形算法内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!