机器学习-支持向量机(SVM)

关于SVM的理论以及推导过程可以参考这篇博文：http://www.cnblogs.com/pinard/p/6097604.html；
这篇博客讲的非常细致，具体到每个公式的推导，但如果想要深入的了解SVM原理还需要自己把公式都推导一遍。
基于Python实现的SVM代码打包地址：https://download.csdn.net/download/pcb931126/10889547

一、简化版的SMO算法进行分类超平面的计算

"""
1.机器学习支持向量机（SVM）
2.使用简化版的SMO算法
3.使用线性核函数
姓名：pcb
时间：2018.12.26
"""
import numpy
from numpy import *
import matplotlib.pyplot as plt

#--------------SMO算法中的辅助函数-------------------------------------------------------
"""
加载数据
"""
def loadDataSet(fileName):
    dataMat=[];labelMat=[]
    fr=open(fileName)
    for line in fr.readlines():
        lineArr=line.strip().split('\t')
        dataMat.append([float(lineArr[0]),float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat,labelMat

"""
在某个区间范围内随机选择一个数
"""
def selectJrand(i,m):
    j=i
    while (j==i):
        j=int(random.uniform(0,m))
    return j

"""
用于调整大于H或者小于L的alpha值
"""
def clipAlpha(aj,H,L):
    if aj>H:
        aj=H
    if L>aj:
        aj=L
    return aj

"""
简化版SMO的伪代码：
    创建一个alpha向0量并将其初始化为0向量
    当迭代次数小于最大迭代次数时（外循环）
        对数据集中的每个数据向量（内循环）：
            如果该向量可以被优化：
               随机选择另外一个数据向量
               同时优化这两个向量
               如果这两个向量都不能被优化，退出内循环
        如果所有向量都没有被优化，增加迭代数目，继续下一次循环 
"""
#简化版的SMO算法（序列最小优化算法）
def smoSimple(dataMatIn,classLabel,C,toler,maxIter):
    """
    :param dataMatIn:   数据集
    :param classLabel:  类别标签
    :param C:           常数C
    :param toler:       容错率
    :param maxIter:     退出前的最大循环次数
    :return:
    """
    dataMatrix=mat(dataMatIn)                              #将列表输入转换成矩阵，简化数学处理操作
    labelMat=mat(classLabel).transpose()                   #将类别列表转置，得到列向量中的每一行都和数据矩阵中的行一一对应
    b=0;
    m,n=shape(dataMatrix)                                  #得到行和列
    alphas=mat(zeros((m,1)))                               #构建一个alpha列矩阵，矩阵中元素都初始化为0
    iter=0                                                 #该变量存储的是在没有任何alpha改变的情况下遍历数据集的次数
                                                           #当变量达到maxIter时，函数结束运行并退出
    while(itertoler)and(alphas[i]>0)):
                j=selectJrand(i,m)    #随机选择第二个alpha的值，在完整的SMO算法中选择第二个alphas时改进
                fXj=float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T))+b #计算第二个alpha的类别
                Ej=fXj-float(labelMat[j])                                               #误差

                #为alphaIold和alphaJold分配内存空间，用于新值和旧值之间的比较
                alphaIold=alphas[i].copy()
                alphaJold=alphas[j].copy()

                #用于修改alphas[j],保证其在0-C之间
                if(labelMat[i]!=labelMat[j]):
                    L=max(0,alphas[j]-alphas[i])
                    H=min(C,C+alphas[j]-alphas[i])
                else:
                    L=max(0,alphas[j]+alphas[i]-C)
                    H=min(C,alphas[j]+alphas[i])

                #如果L=H，则不做任何改变
                if L==H:
                    print('L==H')
                    continue

                #eta是alpha[j]的最优修改量，如果是0，则需要退出当前迭代过程
                eta=2.0*dataMatrix[i,:]*dataMatrix[j,:].T-dataMatrix[i,:]*dataMatrix[i,:].T-\
                    dataMatrix[j,:]*dataMatrix[j,:].T
                if eta>=0:
                    print('eta>=0')
                    continue

                #检车alpha[j]是否有轻微的变化，如果有则退出for循环
                alphas[j]-=labelMat[j]*(Ei-Ej)/eta
                alphas[j]=clipAlpha(alphas[j],H,L)
                if (abs(alphas[j]-alphaJold)<0.00001):
                    print('j not moving enough')
                    continue

                #对i进行修改，修改量与j相同，但方向相反
                alphas[i]+=labelMat[j]*labelMat[i]*(alphaJold-alphas[j])

                #设置常数项
                b1=b-Ei-labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T-\
                    labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                b2=b-Ej-labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T-\
                    labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T

                if (0alphas[i]):
                    b=b1
                elif(0alphas[j]):
                    b=b2
                else:
                    b=(b1+b2)/2.0
                #如果执行到这都不执行continue语句，则说明成功改变了一对alpha,同时可以增加alphaPairsChanged的值
                alphaPairsChanged+=1

                print('iter:%d i:%d,pairs changed %d'%(iter,i,alphaPairsChanged))

        #在for循环外，需要检测alpha值是否做了更新，如果有更新，则需要吧iter设置为0后继续运行程序
        if (alphaPairsChanged==0):
            iter+=1
        else:
            iter=0
        print('iteration number:%d'%iter)

    return b,alphas

#---------------------------------------------------------------------------------------

#----------将得到的支持向量以及分类超平面画出来-------------------------------------------
def plotSupportVector(dataArr,labelArr,alphas,b):
    #s首先得到alphas向量中大于0小于C的，并根据符合要求的alpha找到支持向量
    alpha1=[]                        #存放符合要求的alpha值
    dataArr1=[];labelArr1=[]         #存放支持向量的坐标以及标签
    m,n=shape(alphas)
    xcord1 = [];ycord1 = []              #存放类别为1的数据坐标
    xcord2 = [];ycord2 = []              #存放类别为-1的数据坐标
    xcord3 = [];ycord3 = []              #存放类别为1的支持向量坐标
    xcord4 = [];ycord4 = []              #存放类别为-1的支持向量坐标
    for i in range(m):
        if alphas[i]>0:
            alpha1.extend(alphas[i])
            dataArr1.append(dataArr[i])
            labelArr1.append(labelArr[i])
            if labelArr[i]>0:
                xcord3.append((dataArr[i])[0])
                ycord3.append((dataArr[i])[1])
            else:
                xcord4.append((dataArr[i])[0])
                ycord4.append((dataArr[i])[1])

        if (labelArr[i]>0)and(alphas[i]<=0):
            xcord1.append((dataArr[i])[0])
            ycord1.append((dataArr[i])[1])
        if(labelArr[i]<0)and(alphas[i]<=0):
            xcord2.append((dataArr[i])[0])
            ycord2.append((dataArr[i])[1])

    #计算超平面

    m1=len(alpha1)
    #w =[];w2=[]
    w=mat(zeros((1,2)))
    dataArr2=mat(dataArr1)
    for i in range(m1):
        w+=dataArr2[i]*labelArr1[i]*alpha1[i]

    #得到超平面的系数
    a1=w[0,0]
    a2=w[0,1]

    #画图
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red')
    ax.scatter(xcord3,ycord3,s=50,c='red',marker='x',)
    ax.scatter(xcord2, ycord2, s=30, c='green', marker='s')
    ax.scatter(xcord4,ycord4,s=50,c='green',marker='x')
    ax.set_ylim(-8, 6)  # 设置纵轴范围，单独给图1设置y轴的范围
    x=arange(-2.0, 12.0, 1.0)
    y=(-b - a1 * x) / a2
    ax.plot(x,y.transpose())
    plt.title('Support Vector')
    plt.savefig('简化版SMO支持向量和超平面示意图.png')
    plt.show()
#---------------------------------------------------------------------------------------
def main():
    dataArr,labelArr=loadDataSet('testSet.txt')
    b,alphas=smoSimple(dataArr,labelArr,0.5,0.001,40)
    plotSupportVector(dataArr,labelArr,alphas.getA(),b)
if __name__=='__main__':
    main()

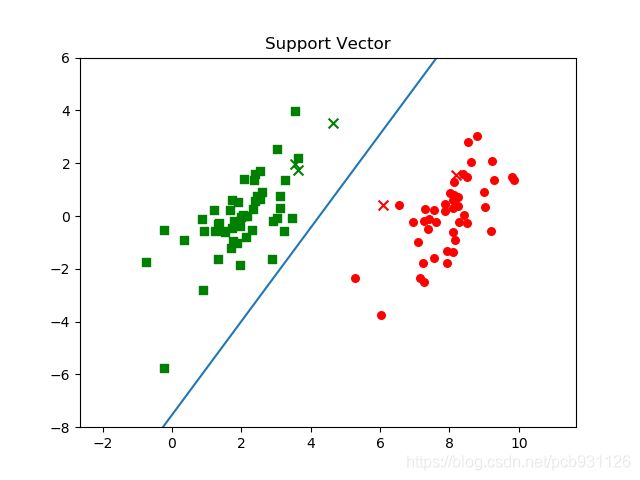
其分类超平面以及支持向量如下图所示(两种不同的颜色代表两类，用×画出来的是支持向量，直线代表计算得到的分类超平面)：

二、将完整版的SMO算法封装到类中进行超平面计算

简化版的SMO算法遍历所有的数据，时间复杂度较高。因此使用完整的SMO算法可实现快速计算分类超平面。

"""
1.机器学习支持向量机SVM
2.使用完整的SMO算法进行加速
3.封装在类中
4.使用线性核函数
姓名：pcb
时间：2018.12.26
"""
import numpy as np
from numpy import *
import matplotlib.pyplot as plt

class optStruct:

    #初始化函数
    def __init__(self,dataMatIn,classLabel,C,toler):
        self.X=dataMatIn                            #m维特征向量
        self.labelMat=classLabel                    #m维标签向量
        self.C=C                                    #常数C
        self.tol=toler                              #容错率
        self.m=shape(dataMatIn)[0]
        self.alphas=mat(zeros((self.m,1)))          #建立并初始化alphas举证
        self.b=0
        self.eCache=mat(zeros((self.m,2)))          #第一列给出是否有效的标志位，第二列给出实际的E值

    #计算E值并返回结果
    def calcEk(self,k):
        fXk=float(multiply(self.alphas,self.labelMat).T*(self.X*self.X[k,:].T))+self.b #用于计算第k个样本的类别预测
        Ek=fXk-float(self.labelMat[k])                                                 #预测结果和真实结果的误差
        return Ek

    #在某个区间范围内随机选择一个数
    def selectJrand(self,i, m):
        j = i
        while (j == i):
            j = int(random.uniform(0, m))
        return j

    #用于调整大于H或者小于L的alpha值
    def clipAlpha(self,aj, H, L):
        if aj > H:
            aj = H
        if L > aj:
            aj = L
        return aj

    #用于选择第二个alphas的值（内循环中的启发式方法）
    #选择合适的第二个alphas值以保证在每次优化中采用最大的步长
    def selectJ(self,i,Ei):
        maxK=-1;maxDeltaE=0;Ej=0
        self.eCache[i]=[1,Ei]                                        #将输入值在缓存在设置为有效
        validEcacheList=nonzero(self.eCache[:,0].A)[0]               #构建非零表，返回非零E值所对应的alphas值
        if (len(validEcacheList))>1:
            for k in validEcacheList:
                if k==i:
                    continue
                Ek=self.calcEk(k)
                deltaE=abs(Ei-Ek)
                if (deltaE>maxDeltaE):                             #在所有值上进行循环，并选择其中使得改变最大的那个值
                    maxK=k
                    maxDeltaE=deltaE;
                    Ej=Ek
            return maxK,Ej

        else:                                                      #如果这是一次循环的话就随机选择一个alphas值进行计算
            j=self.selectJrand(i,self.m)
            Ej=self.calcEk(j)
        return j,Ej

    #计算误差值并存入缓存中，再对alphas值进行优化时会用到这个值
    def updataEk(self,k):
        Ek=self.calcEk(k)
        self.eCache[k]=[1,Ek]

    #寻找决策边界
    def innerL(self,i):
        Ei=self.calcEk(i)

        if((self.labelMat[i]*Ei<-self.tol)and(self.alphas[i]self.tol)and(self.alphas[i]>0)):

            j,Ej=self.selectJ(i,Ei)                      #第二个alphas选择中的启发方式
            alphaIold=self.alphas[i].copy()
            alphaJold=self.alphas[j].copy()

            if(self.labelMat[i]!=self.labelMat[j]):
                L=max(0,self.alphas[j]-self.alphas[i])
                H=min(self.C,self.C+self.alphas[j]-self.alphas[i])
            else:
                L=max(0,self.alphas[j]+self.alphas[i]-self.C)
                H=min(self.C,self.alphas[j]+self.alphas[i])

            if L==H:
                print('L==H')
                return 0

            eta=2.0*self.X[i,:]*self.X[j,:].T-self.X[i,:]*self.X[i,:].T-self.X[j,:]*self.X[j,:].T
            if eta>=0:
                print('eta>=0')
                return 0

            #更新误差缓存
            self.alphas[j]-=self.labelMat[j]*(Ei-Ej)/eta
            self.alphas[j]=self.clipAlpha(self.alphas[j],H,L)
            self.updataEk(j)

            if(abs(self.alphas[j]-alphaJold)<0.00001):
                print('j not moving enough')
                return 0

            self.alphas[i]+=self.labelMat[j]*self.labelMat[i]*(alphaJold-self.alphas[j])
            self.updataEk(i)

            #计算b1,b2的值
            b1=self.b-Ei-self.labelMat[i]*(self.alphas[i]-alphaIold)*self.X[i,:]*self.X[i,:].T-\
               self.labelMat[j]*(self.alphas[j]-alphaJold)*self.X[i,:]*self.X[j,:].T
            b2=self.b-Ej-self.labelMat[i]*(self.alphas[i]-alphaIold)*self.X[i,:]*self.X[j,:].T-\
                self.labelMat[j]*(self.alphas[j]-alphaJold)*self.X[j,:]*self.X[j,:].T

            if (0self.alphas[i]):
                self.b=b1
            elif(0self.alphas[j]):
                self.b=b2
            else:
                self.b=(b1+b2)/2.0
            a1, a2 = shape(mat(self.b))
            if (a1 != 1) or (a2 != 1):
                a = 111
            return 1

        else:
            return 0

    #完整的PlattSMO的外循环代码
    def smoP(self,dataMatIn,classLabels,C,tolar,maxIter,kTup=('lin',0)):

        iter=0
        entireSet=True
        alphaPairsChanged=0

        #当迭代次数超过最大指定值，或遍历整个集合都未对任意的alpha进行修改就退出循环
        #这里的一次迭代定义为一次循环过程，而不管该循环具体做了什么，如果优化过程中存在波动就停止
        while(iter0)or(entireSet)):
            alphaPairsChanged=0
            if entireSet:
                #遍历所有可能的alphas的值
                for i in range(self.m):
                    alphaPairsChanged+=self.innerL(i)       #通过调用选择第二个alphas,并在可能是对其进行优化
                    print('fullSet,iter:%d i:%d,pairs changed %d'%(iter,i,alphaPairsChanged))
                iter+=1
            else:
                nonBoundIs=nonzero((self.alphas.A>0)*(self.alphas.A0:
            classifyResult=1
        else:
            classifyResult=-1

        return classifyResult
    #----------将得到的支持向量以及分类超平面画出来-------------------------------------------
    def plotSupportVector(self,dataArr,labelArr,alphas,b):
        #s首先得到alphas向量中大于0小于C的，并根据符合要求的alpha找到支持向量
        alpha1=[]                        #存放符合要求的alpha值
        dataArr1=[];labelArr1=[]         #存放支持向量的坐标以及标签
        m,n=shape(alphas)
        xcord1 = [];ycord1 = []              #存放类别为1的数据坐标
        xcord2 = [];ycord2 = []              #存放类别为-1的数据坐标
        xcord3 = [];ycord3 = []              #存放类别为1的支持向量坐标
        xcord4 = [];ycord4 = []              #存放类别为-1的支持向量坐标
        for i in range(m):
            if alphas[i]>0:
                alpha1.extend(alphas[i])
                dataArr1.append(dataArr[i])
                labelArr1.append(labelArr[i])
                if labelArr[i]>0:
                    xcord3.append((dataArr[i])[0])
                    ycord3.append((dataArr[i])[1])
                else:
                    xcord4.append((dataArr[i])[0])
                    ycord4.append((dataArr[i])[1])

            if (labelArr[i]>0)and(alphas[i]<=0):
                xcord1.append((dataArr[i])[0])
                ycord1.append((dataArr[i])[1])
            if(labelArr[i]<0)and(alphas[i]<=0):
                xcord2.append((dataArr[i])[0])
                ycord2.append((dataArr[i])[1])

        #计算超平面

        m1=len(alpha1)
        #w =[];w2=[]
        w=mat(zeros((1,2)))
        dataArr2=mat(dataArr1)
        for i in range(m1):
            w+=dataArr2[i]*labelArr1[i]*alpha1[i]

        #得到超平面的系数
        a1=w[0,0]
        a2=w[0,1]

        #画图
        fig = plt.figure()
        ax = fig.add_subplot(111)
        ax.scatter(xcord1, ycord1, s=30, c='red')
        ax.scatter(xcord3,ycord3,s=50,c='red',marker='x',)
        ax.scatter(xcord2, ycord2, s=30, c='green', marker='s')
        ax.scatter(xcord4,ycord4,s=50,c='green',marker='x')
        ax.set_ylim(-8, 6)  # 设置纵轴范围，单独给图1设置y轴的范围
        x=arange(-2.0, 12.0, 1.0)
        y=(-b - a1 * x) / a2
        ax.plot(x,y.transpose())
        plt.title('Support Vector')
        plt.savefig('SVM支持向量和超平面示意图.png')
        plt.show()
    #---------------------------------------------------------------------------------------

#加载数据
def loadDataSet(fileName):
    dataMat = [];
    labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat
def main():
    dataArr,lebalArr=loadDataSet('testSet.txt')
    oS=optStruct(mat(dataArr),mat(lebalArr).transpose(),0.6,0.001)           #定义一个类对象
    b,alphas=oS.smoP(dataArr,lebalArr,0.6,0.001,40)
    classifyResult=oS.classificationSVM(dataArr[20])
    print(classifyResult)
    oS.plotSupportVector(dataArr,lebalArr,alphas.getA(),b)
if __name__=='__main__':
    main()

完整版的SMO算法所需要的时间较少，分类效果如下：

三、在复杂数据上(非线性可分)使用核函数，并用其对手写体进行识别

"""
1.机器学习支持向量机SVM
2.使用完整的SMO算法进行加速
3.封装在类中
4.使用径向基函数(RBF)或者线性核函数
5.使用SVM进行手写体数字的识别

姓名：pcb
时间：2018.12.26
"""
import numpy as np
from numpy import *
import matplotlib.pyplot as plt
from os import listdir

class optStruct:

    #初始化函数
    def __init__(self,dataMatIn,classLabel,C,toler,kTup):
        self.X=dataMatIn                            #m维特征向量
        self.labelMat=classLabel                    #m维标签向量
        self.C=C                                    #常数C
        self.tol=toler                              #容错率
        self.m=shape(dataMatIn)[0]
        self.alphas=mat(zeros((self.m,1)))          #建立并初始化alphas举证
        self.b=0
        self.eCache=mat(zeros((self.m,2)))          #第一列给出是否有效的标志位，第二列给出实际的E值
        self.K=mat(zeros((self.m,self.m)))
        for i in range(self.m):
            self.K[:,i]=self.kernelTrans(self.X,self.X[i,:],kTup)

    def kernelTrans(self,X,A,kTup):
        m,n=shape(X)
        K=mat(zeros((m,1)))
        if kTup=='lin':
            K=X*A.T
        elif kTup[0]=='rbf':
            for j in range(m):
                daltRow=X[j,:]-A
                K[j]=daltRow*daltRow.T
            K=exp(K/(-1*kTup[1]**2))
        else:
            raise NameError('Houston We Have a Problem--That Kernel is not recognized')
        return K

    #计算E值并返回结果
    def calcEk(self,k):
        fXk=float(multiply(self.alphas,self.labelMat).T*(self.K[:,k])+self.b) #用于计算第k个样本的类别预测
        Ek=fXk-float(self.labelMat[k])                                                 #预测结果和真实结果的误差
        return Ek

    #在某个区间范围内随机选择一个数
    def selectJrand(self,i, m):
        j = i
        while (j == i):
            j = int(random.uniform(0, m))
        return j

    #用于调整大于H或者小于L的alpha值
    def clipAlpha(self,aj, H, L):
        if aj > H:
            aj = H
        if L > aj:
            aj = L
        return aj

    #用于选择第二个alphas的值（内循环中的启发式方法）
    #选择合适的第二个alphas值以保证在每次优化中采用最大的步长
    def selectJ(self,i,Ei):
        maxK=-1;maxDeltaE=0;Ej=0
        self.eCache[i]=[1,Ei]                                        #将输入值在缓存在设置为有效
        validEcacheList=nonzero(self.eCache[:,0].A)[0]               #构建非零表，返回非零E值所对应的alphas值
        if (len(validEcacheList))>1:
            for k in validEcacheList:
                if k==i:
                    continue
                Ek=self.calcEk(k)
                deltaE=abs(Ei-Ek)
                if (deltaE>maxDeltaE):                             #在所有值上进行循环，并选择其中使得改变最大的那个值
                    maxK=k
                    maxDeltaE=deltaE;
                    Ej=Ek
            return maxK,Ej

        else:                                                      #如果这是一次循环的话就随机选择一个alphas值进行计算
            j=self.selectJrand(i,self.m)
            Ej=self.calcEk(j)
        return j,Ej

    #计算误差值并存入缓存中，再对alphas值进行优化时会用到这个值
    def updataEk(self,k):
        Ek=self.calcEk(k)
        self.eCache[k]=[1,Ek]

    #寻找决策边界
    def innerL(self,i):
        Ei=self.calcEk(i)

        if((self.labelMat[i]*Ei<-self.tol)and(self.alphas[i]self.tol)and(self.alphas[i]>0)):

            j,Ej=self.selectJ(i,Ei)                      #第二个alphas选择中的启发方式
            alphaIold=self.alphas[i].copy()
            alphaJold=self.alphas[j].copy()

            if(self.labelMat[i]!=self.labelMat[j]):
                L=max(0,self.alphas[j]-self.alphas[i])
                H=min(self.C,self.C+self.alphas[j]-self.alphas[i])
            else:
                L=max(0,self.alphas[j]+self.alphas[i]-self.C)
                H=min(self.C,self.alphas[j]+self.alphas[i])

            if L==H:
                print('L==H')
                return 0

            eta=2.0*self.K[i,j]-self.K[i,i]-self.K[j,j]
            if eta>=0:
                print('eta>=0')
                return 0

            #更新误差缓存
            self.alphas[j]-=self.labelMat[j]*(Ei-Ej)/eta
            self.alphas[j]=self.clipAlpha(self.alphas[j],H,L)
            self.updataEk(j)

            if(abs(self.alphas[j]-alphaJold)<0.00001):
                print('j not moving enough')
                return 0

            self.alphas[i]+=self.labelMat[j]*self.labelMat[i]*(alphaJold-self.alphas[j])
            self.updataEk(i)

            #计算b1,b2的值
            b1=self.b-Ei-self.labelMat[i]*(self.alphas[i]-alphaIold)*self.K[i,i]-\
               self.labelMat[j]*(self.alphas[j]-alphaJold)*self.K[i,j]
            b2=self.b-Ej-self.labelMat[i]*(self.alphas[i]-alphaIold)*self.K[i,j]-\
                self.labelMat[j]*(self.alphas[j]-alphaJold)*self.K[j,j]

            if (0self.alphas[i]):
                self.b=b1
            elif(0self.alphas[j]):
                self.b=b2
            else:
                self.b=(b1+b2)/2.0
            a1, a2 = shape(mat(self.b))
            if (a1 != 1) or (a2 != 1):
                a = 111
            return 1

        else:
            return 0

    #完整的PlattSMO的外循环代码
    def smoP(self,dataMatIn,classLabels,C,tolar,maxIter):

        iter=0
        entireSet=True
        alphaPairsChanged=0

        #当迭代次数超过最大指定值，或遍历整个集合都未对任意的alpha进行修改就退出循环
        #这里的一次迭代定义为一次循环过程，而不管该循环具体做了什么，如果优化过程中存在波动就停止
        while(iter0)or(entireSet)):
            alphaPairsChanged=0
            if entireSet:
                #遍历所有可能的alphas的值
                for i in range(self.m):
                    alphaPairsChanged+=self.innerL(i)       #通过调用选择第二个alphas,并在可能是对其进行优化
                    print('fullSet,iter:%d i:%d,pairs changed %d'%(iter,i,alphaPairsChanged))
                iter+=1
            else:
                nonBoundIs=nonzero((self.alphas.A>0)*(self.alphas.A0:
            classifyResult=1
        else:
            classifyResult=-1

        return classifyResult

    #使用核函数进行分类的径向基测试函数
    def testRbf(self,dataArr1,labelArr1,dataArr2,labelArr2,alphas,b,k1=1.4):
        datMat1=mat(dataArr1);labelMat=mat(labelArr1).transpose()
        svInd=nonzero(alphas.A>0)[0]
        sVs=datMat1[svInd]
        labelSV=labelMat[svInd]
        print('there are %d Support Vectors'%shape(sVs)[0])
        m,n=shape(datMat1)
        errorCountTrain=0
        for i in range(m):
            kernelEval=self.kernelTrans(sVs,datMat1[i,:],('rbf',k1))
            predict=kernelEval.T*multiply(labelSV,alphas[svInd])+b
            if sign(predict)!=sign(labelArr1[i]):
                errorCountTrain+=1
        print('the trianing error rate is :%f'%(float(errorCountTrain)/m))

        errorCountTest=0
        datMat2=mat(dataArr2);labelMat2=mat(labelArr2).transpose()
        #sVs = datMat2[svInd]
        #labelSV = labelMat2[svInd]
        m,n=shape(datMat2)
        for i in range(m):
            kernelEval=self.kernelTrans(sVs,datMat2[i,:],('rbf',k1))
            predict=kernelEval.T*multiply(labelSV,alphas[svInd])+b
            if sign(predict)!=sign(labelArr2[i]):
                errorCountTest+=1
        print('the test error rate is :%f'%(float(errorCountTest)/m))

    #----------将得到的支持向量以及分类超平面画出来-------------------------------------------
    def plotSupportVector(self,dataArr,labelArr,alphas,b):
        #s首先得到alphas向量中大于0小于C的，并根据符合要求的alpha找到支持向量
        alpha1=[]                        #存放符合要求的alpha值
        dataArr1=[];labelArr1=[]         #存放支持向量的坐标以及标签
        m,n=shape(alphas)
        xcord1 = [];ycord1 = []              #存放类别为1的数据坐标
        xcord2 = [];ycord2 = []              #存放类别为-1的数据坐标
        xcord3 = [];ycord3 = []              #存放类别为1的支持向量坐标
        xcord4 = [];ycord4 = []              #存放类别为-1的支持向量坐标
        for i in range(m):
            if alphas[i]>0:
                alpha1.extend(alphas[i])
                dataArr1.append(dataArr[i])
                labelArr1.append(labelArr[i])
                if labelArr[i]>0:
                    xcord3.append((dataArr[i])[0])
                    ycord3.append((dataArr[i])[1])
                else:
                    xcord4.append((dataArr[i])[0])
                    ycord4.append((dataArr[i])[1])

            if (labelArr[i]>0)and(alphas[i]<=0):
                xcord1.append((dataArr[i])[0])
                ycord1.append((dataArr[i])[1])
            if(labelArr[i]<0)and(alphas[i]<=0):
                xcord2.append((dataArr[i])[0])
                ycord2.append((dataArr[i])[1])

        #计算超平面
        m1=len(alpha1)
        #w =[];w2=[]
        w=mat(zeros((1,2)))
        dataArr2=mat(dataArr1)
        for i in range(m1):
            w+=dataArr2[i]*labelArr1[i]*alpha1[i]

        #得到超平面的系数
        a1=w[0,0]
        a2=w[0,1]

        #画图
        fig = plt.figure()
        ax = fig.add_subplot(111)
        ax.scatter(xcord1, ycord1, s=30, c='red')
        ax.scatter(xcord3,ycord3,s=50,c='red',marker='x',)
        ax.scatter(xcord2, ycord2, s=30, c='green', marker='s')
        ax.scatter(xcord4,ycord4,s=50,c='green',marker='x')
        ax.set_ylim(-8, 6)  # 设置纵轴范围，单独给图1设置y轴的范围
        x=arange(-2.0, 12.0, 1.0)
        y=(-b - a1 * x) / a2
        ax.plot(x,y.transpose())
        plt.title('Support Vector')
        plt.savefig('SVM支持向量和超平面示意图.png')
        plt.show()
    #---------------------------------------------------------------------------------------
    #使用SVM对手写体进行测试
    def testDigits(self,dataArr1,labelArr1,dataArr2,labelArr2,alphas,b,k1=10):
        datMat=mat(dataArr1);labelMat=mat(labelArr1).transpose()
        svInd=nonzero(alphas.A>0)[0]
        sVs=datMat[svInd]
        labelSV=labelMat[svInd]
        print('There are %d Support Vectors'%shape(sVs)[0])
        m,n=shape(datMat)
        errorCount=0
        for i in range(m):
            kernelEval=self.kernelTrans(sVs,datMat[i,:],('rbf',k1))
            predict=kernelEval.T*multiply(labelSV,alphas[svInd])+b
            if sign(predict)!=sign(labelArr1[i]):
                errorCount+=1
        print('the trianing error rate is:%f'%(float(errorCount)/m))

        errorCountTest=0
        datMat2=mat(dataArr2);labelMat2=mat(labelArr2).transpose()
        m,n=shape(datMat2)
        for i in range(m):
            kernelEval=self.kernelTrans(sVs,datMat2[i,:],('rbf',k1))
            predict=kernelEval.T*multiply(labelSV,alphas[svInd])+b
            if sign(predict)!=sign(labelArr2[i]):
                errorCountTest+=1
        print('the test error rate is :%f'%(float(errorCountTest)/m))

 #加载手写体图像数据
def loadImages(dirName):
    hwLabels=[]
    trainingFileList=listdir(dirName)
    m=len(trainingFileList)
    trainingMat=zeros((m,1024))
    for i in range(m):
        fileNameStr=trainingFileList[i]
        fileStr=fileNameStr.split('.')[0]
        classNumStr=int(fileStr.split('_')[0])
        if classNumStr==9:
            hwLabels.append(-1)
        else:
            hwLabels.append(1)
        trainingMat[i,:] =img2vector('%s/%s'%(dirName,fileNameStr))
    return trainingMat,hwLabels

#将图像转化成向量
def img2vector(filename):
    returnVec = zeros((1, 1024))  # 将图像32*32的二进制图像矩阵转换为1*1024的向量
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVec[0, 32 * i + j] = int(lineStr[j])
    return returnVec

#加载数据
def loadDataSet(fileName):
    dataMat = [];
    labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat

def main():
# #1.---------------在复杂的数据集上使用SVM进行分类------------------------------------------------
#     dataArr1,lebalArr1=loadDataSet('testSetRBF.txt')
#     dataArr2,lebalArr2=loadDataSet('testSetRBF2.txt')
#     k1=1.4
#     oS=optStruct(mat(dataArr1),mat(lebalArr1).transpose(),200,0.0001,('rbf',k1))#定义一个类对象
#     b,alphas=oS.smoP(dataArr1,lebalArr1,200,0.001,10000)
#     oS.testRbf(dataArr1,lebalArr1,dataArr2,lebalArr2,alphas,b)
# #---------------------------------------------------------------------------------------------

#2.----------------使用SVM进行手写体问题识别----------------------------------------------------
    dataArr1,labelArr1=loadImages('trainingDigits')
    dataArr2,labelArr2=loadImages('testDigits')
    k1=10
    oS=optStruct(mat(dataArr1),mat(labelArr1).transpose(),200,0.0001,('rbf',k1))#定义一个类对象
    b,alphas=oS.smoP(dataArr1,labelArr2,200,0.001,10000)
    oS.testDigits(dataArr1,labelArr1,dataArr2,labelArr2,alphas,b)
#--------------------------------------------------------------------------------------------

if __name__=='__main__':
    main()

训练集和测试集的分类效果如下图所示，训练集的错位率为0%，测试集的错误率为0.53%，而使用K邻近算法的错误率在1.3%。