数算部分-----第一节----算法的时空复杂度

大家好，我还是那个快乐学编程，学到无极限的@jxwd~~~

题外话：

在接下来的2个月多里，小编会持续推出数据结构于算法以及C++的内容。关注我，订阅专栏，就能持续看到我的文章啦~~~

对于数据结构与算法，小编仍会采用章节式的体裁来介绍讲解。

我们把数据结构与算法和C++的学习融合在一起。

即先学一部分的数据结构与算法的基础内容（学到二叉树），这之前的代码我们都将以C语言的形式实现，然后在此基础上去学习C++，包括它的各种语法和STL，然后再用C++来完成后面部分复杂的数据结构的学习（因为C不够灵活）。

本节为数据结构于算法的第一节

所有的数据结构章节均对《大话数据结构》和《数据结构与算法分析》有一定参考。

来一波口号：jxwd，让你服气，拒绝水文，从我做起！~~~

看我的博客，就基本不用啃读课本啦

看了我的博客，课本你会当小说一样的把它顺畅地看完

当然，前提是我说的你也要能够接受。放心，只要你认真读下去，你就能非常容易地看懂

话不多说，我们正式开始。

目录

数据结构前言：

——算法的时空复杂度

算法效率

算法的特性

算法的时间复杂度

算法的空间复杂度

---

数据结构前言：

学习数据结构之前，需要问一问自己，何为数据结构？

实际上，数据结构，Data Structure, 指的就是计算机存储、组织数据的一种方式。并且可以理解为，这些数据的元素间有着特定关系。而这些数据包含其特定关系的集合，就叫数据结构。

那算法呢？我们在学习数据结构的时候，总能听到：数据结构与算法这样的说法。

即意为数据结构于算法不分家。

那么算法(Algorithm)简单来说就是经过一系列的计算步骤，达到输入与预期输出之间的关系。

那么数据结构有多重要？我们不从学校考试、绩点等方面来分析，这样显得格局太小且没有意义。我们从个人的工作中来说，数据结构在校招、笔面试是必考的环节，它体现着一个人的算法功底以及发展潜力。在日后的工作中，不会用数据结构，那....只能说...可能比较惨。（不排除个例，如果你不信的话你可以去吃个螃蟹哈~~~）（可以参见《大话数据结构》中作者举的例子）

所以说，数据结构与算法是一门极其极其重要的课程！！！

好，我们正式进入第一章的学习

——算法的时空复杂度

对于很多学校和老师来说，这一节是直接不讲的。

但我想说，这一节，正是算法的核心。

甚至于比我们后面所有学的数据结构以及算法的知识都要重要。

它对于我们代码的优化、代码的规范和简化、代码的书写习惯都提升了一个更高的要求。

它往往体现在一些看似“微不足道”的地方。

但是，当一个项目有几万行、几百万行代码的时候，就会被无限放大。

可以想象，

一种算法for循环套着for循环又套装for循环，另外的一种几句话搞定。

一种算法是要2^n次，而另外一种算法只要处理logn次（注：我们本章所有的log均指以2为底），当n趋向于无穷时，二者所需的时间可谓千差万别。

我们本章暂时先不探讨代码风格，就只谈算法的优化和简化。

我们先来说说什么叫算法的复杂度。

算法的复杂度包含算法的时间复杂度和算法的空间复杂度。我们将分别详细地探讨这两个概念。

先打个预防针，这一节其实概念性的东西比较多，实操性比较弱，但我们从下一节顺序表开始，将会在教大家思路的同时，教会大家代码的实现。

我们目前的数据结构用的是C语言来实现。

算法效率

算法效率分析分为两种：第一种是时间效率，第二种是空间效率。

时间效率被称为时间复杂度，而空间效率被称作空间复杂度。 时间复杂度主要衡量的是一个算法的运行速度。

空间复杂度主要衡量一个算法所需要的额外空间。

在计算机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。

但是经过计算机行业的迅速发展，计算机的存储容量已经达到了很高的程度。

所以我们如今已经不需要再特别关注一个算法的空间复杂度。

算法的特性

这里我们简单提一下：

1.输入：在算法中可以有零个或者多个输入

2.输出：在算法中至少有一个或者多个输出

3.有穷性：在执行有限的步骤之后，自动结束不会出现无限循环并且每一个步骤在可接受的时间内完成

4.确定性：算法的每一个步骤都具有确定的含义，不会出现二义性

 5.可行性：算法的每一步都必须是可行的，也就是说，每一步都能够通过执行有限的次数完成
 

算法的时间复杂度

在理解这个概念之前，我们需要知道，什么叫做好的算法？

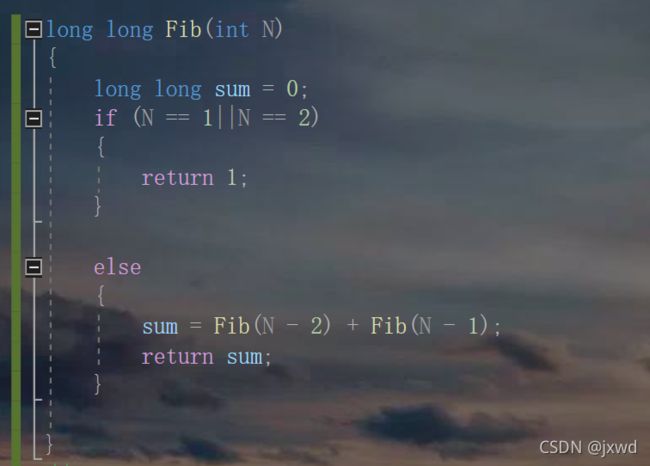
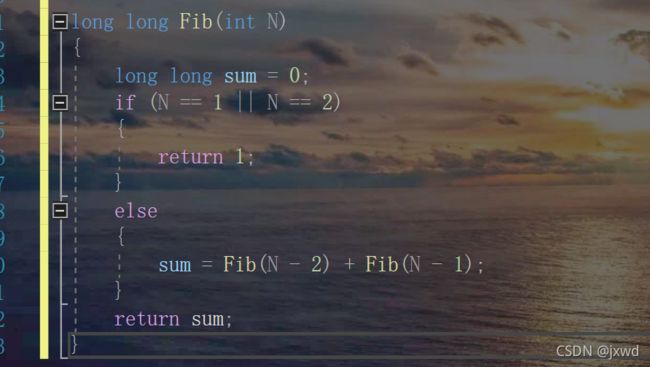
我们还记得计算斐波那契数列的时候所用的算法么？

我们当时是怎么做的？

大概率，我们是用下面的代码实现的：

 代码运行起来之后，当我们输入10,20,30等小数字的时候，答案确实会一下子就出来了。

但是，当我们输入50的时候，它迟迟不出结果（下图视频以三倍速播放）：

有兴趣的小伙伴可以试一下，应该是要十几分钟就能出来了

（这个图gif太不清楚了~~~~555）

为什么会这样？原因在于它的算法的效率，真的是太太太太太低了，算法的时间复杂度巨高。学完本章，你就能更深层次地理解这其中的原因了。

接下来，我们就要来了解一下，什么叫做算法的时间复杂度或者说时间效率？

 （图）

（源自百度百科）

从字面意思去理解的话，实际上就是计算算法的运算效率的函数，它也就是这个意思。

说是时间复杂度，但是我们不可能去真的计算每个程序每一次运行的时间。

因为每一次运行的时间不仅仅与你设计的代码有关，还与你的电脑的性能、电脑当前的CPU运行的速度等等都有关系。所以，计算每一次运行的时间，意义就不大了。

那我们算什么？

实际上，我们比较的，可以认为是算法过程中的大头，主要矛盾。

我们用大O渐进表示法来表示。

至于大O渐进法到底是什么？

我们回到概念上去，我们刚刚说算法的时间复杂度是计算算法的运算效率的函数。

假设，我们用f(n)来表示一个程序要执行的语句次数，n可以先理解为函数f的规模。那么我们将会得到f(n)关于规模n的一个函数。

我们不要光干讲概念，来举个例子吧：

在数学中，我们如果有这么一个表达式：

F（n）=n*n + n + 5。

当n取100时，n*n为10000，而后面的只有105，105相较于10000而言，非常的小，如果n再大，那么n*n的值比n+5大的更多。n+5会相较于n*n而言会更小。小到可以忽略不计。那么n如果还要再大，后面的n+5就会更更小……

所以决定F（n)的阶数的是前面的n*n，后面的n+5在n很大的时候，相较于n*n，对于结果的影响便会微不足道。

我们对于这样的F(n)，取能主要影响结果的那一项，即n^2(n*n)，那么用大O进阶表示法的话就是O(n^2)。

同样的道理，我们可以再举一个例子：

F(n) = 1/2*n + 5; 这里影响最终结果的一项（或者可以直接理解为次数最高的一项）为1/2*n，然后将前面的系数变成1（因为我们只抓”主要矛盾、关键部分“），最终，得到的大O阶为O（n）。

那如果F(n) = 5呢？对于常数函数，我们就用O(1)来表示。

那么我们总结一下：

大O符号（Big O notation）：

是用于描述函数渐进行为的数学符号。

推导大O阶方法：

1、用常数1取代运行时间中的所有加法常数。

2、在修改后的运行次数函数中，只保留最高阶项。

3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

好。我们再用具体的代码来举例。

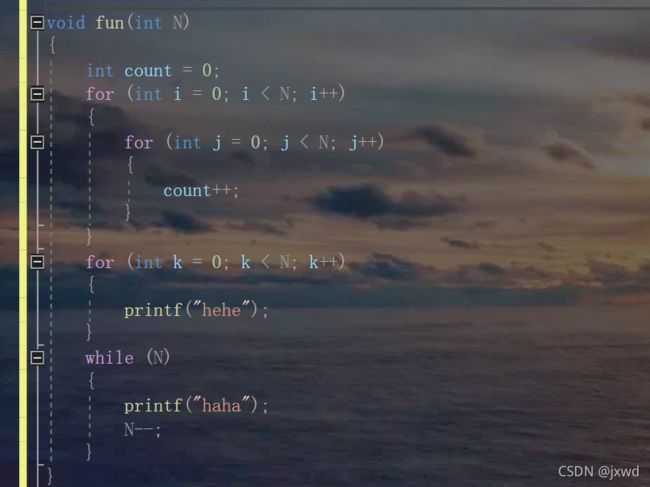
请看：（例1：）

 我如果调用这么一个函数，请问它的时间复杂度是多少？（用大O表示）

首先，应当将其表达式写出来。

它的表达式可以表示为：f(n) = 1+n*n+n+2n。整理一下，得：f(n)=n^2+3n+1。

所以，得到它的时间复杂度为O(N^2)。

我们再来看几个例子：

 （例二：）

请问，这个函数的时间复杂度是多少？

同样的道理，我们还是先写出表达式：f(n,m)=n+m+1;1相对于m和n对表达式的影响很小，所以可以忽略不计。而由于我们并不知道m与n之间的关系，所以我们应当予以保留。即该函数的时间复杂度为O(m+n)

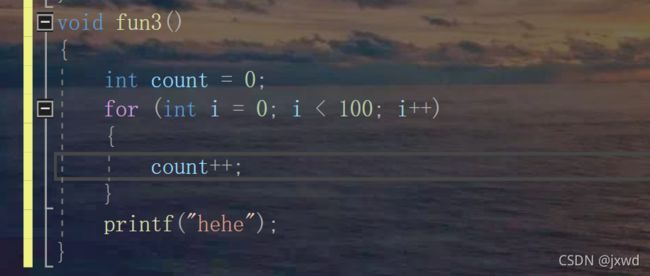
例三：

我们再来看一个例子：

请问这个算法的时间复杂度是多少？

还是先算表达式：f(n)=1+100+1=102;    常数阶，所以为O(1)；

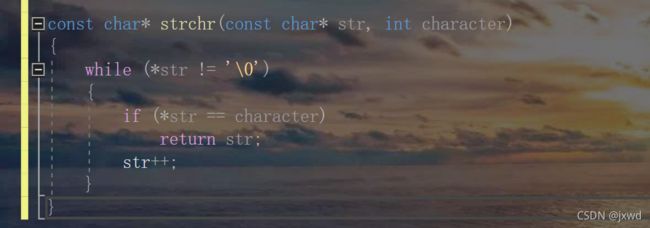
例四：（作用是在一个字符串中找到我们想要的元素）

 假如我们传入的str为一个字符串，字符串的长度为n，那么请问该函数的时间复杂度为多少？

其实，这样的情况分为很多种，换句话说，看运气。

如果运气好，我们一次就能找到。

如果运气不好，要遍历完才能判断能否找到，就是说要到第n个才能找到（或找不到）。

还可以是平均的情况，就是n/2次。

那么我们算这个函数的复杂度应该怎么弄呢？实际上，我们在算复杂度的时候，是按照最坏的情况算的。最坏情况运行时间是一种保证，那就是运行时间将不会再坏了，在应用中也是一种需求。这是一种确定的情况。所以我们在一般没有特殊说明的情况下，都是按照最坏的情况来算。

所以，上述的算法的时间复杂度为O(n)

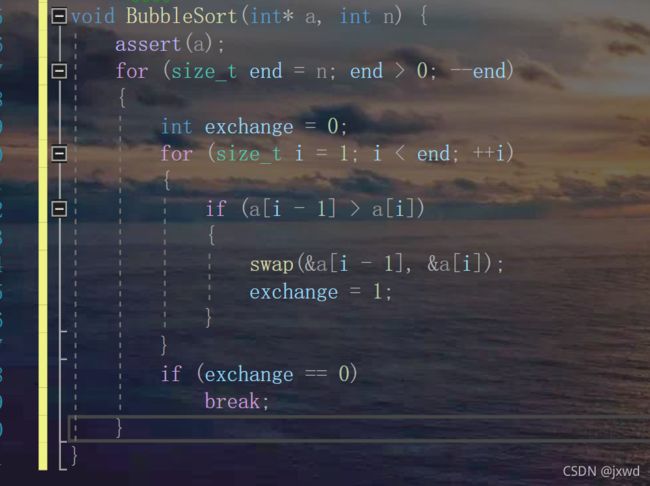
例五：

请问该冒泡排序算法的时间复杂度是多少？

我们还是把表达式写出来：

f(n)=(n-1)+(n-2)+(n-3)+(n-4)+...+1=n*(n-1)/2

所以，它的算法的时间复杂度应当是O(n^2)

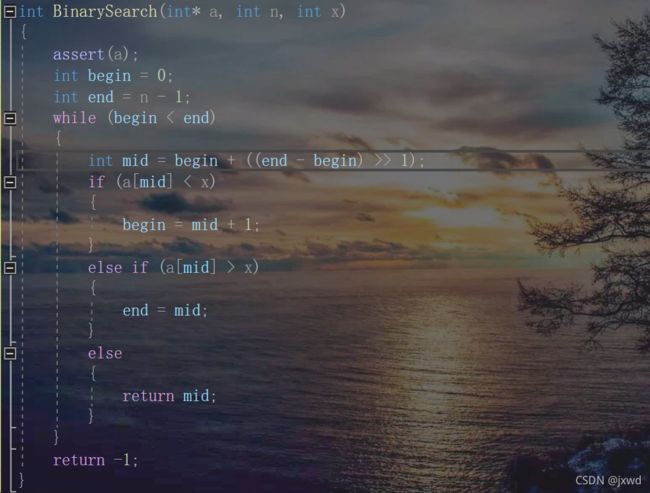
例六：

 该二分查找的算法的时间复杂度是多少？

同样，还要分最好和最坏的情况来讨论：

最好的情况：一次就找到，那就是O(1);

最坏的情况：最后一次才找到。假设找了x次，有n个元素，则n/2/2/2/2.../2=1，那么/2这个运算进行了x次。所以n = 2^x，所以x = logn。

因此，该二分查找的算法的复杂度为（logn）

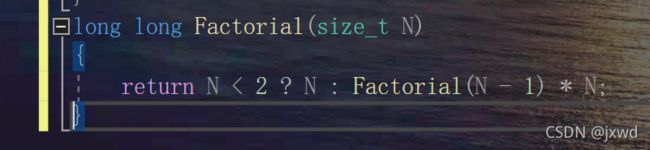
例七：

 请问该算法的复杂度为多少？

对于递归的算法复杂度，它等于    递归次数*每次递归函数中的次数

那么对于这个例子，它递归了多少次？

Fac(N)->Fac(N-1)->Fac(N-2)->Fac(N-3)->Fac(N-4).....->Fac(1)    递归了n次。

故f（n) = 1*n

所以算法复杂度为O(n)

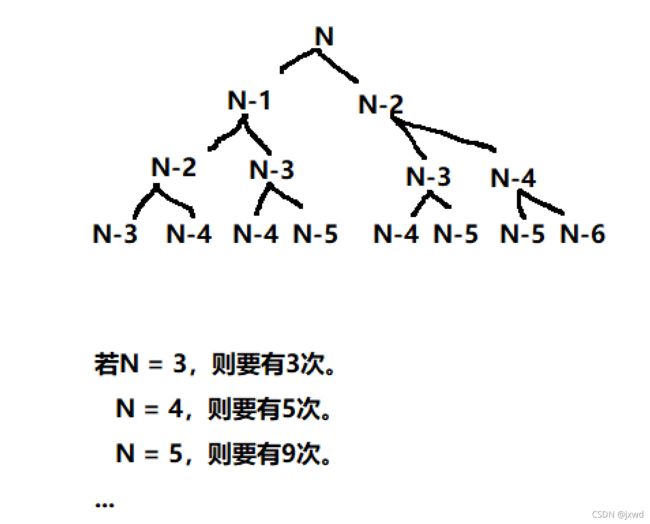
例八：

 我们回到当初的那个例子，来看看它的算法复杂度是多少。

 

 实际上，它的次数是一个完全二叉树的形式（我们后面会讲）。那么它要算的次数就是完全二叉树的节点的个数。所以它要运算的次数为f(n) = 2^(n-1) - 1 -X(X为完全二叉树与同等深度的满二叉树的节点的个数之差，一个常数），这个我们后面也会讲。

所以，它的时间复杂度为O(2^n)。

所以，我们刚刚在算50的斐波那契数列时，可想而知，得到的数字将会是一个天文数字~~~~~ 

关于算法的时间复杂度，我们就先说到这里。

下面，我们再来说说算法的空间复杂度

算法的空间复杂度

类比于时间复杂度，对于算法的空间复杂度，我们也不会去计算每个算法都开辟了多少字节的空间。因为这个也没太大意义，所以空间复杂度算的是变量的个数。

空间复杂度计算规则基本跟实践复杂度类似，也使用大O渐进表示法。

我们还是通过举几个例子来说明：

例一：

 还是来看刚刚的冒泡排序：

请问，它的空间复杂度是多少？

实际上，它创建的变量就一个exchange，就是说，它的变量的数量是一个常数阶。

所以，它的空间复杂度为O(1)

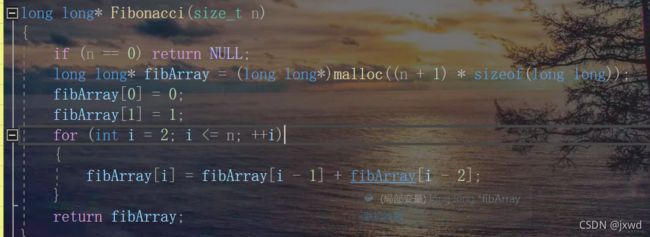
例二：

来看这么个斐波那契数列的算法。

我们可以看出，我们用malloc创建了n+1个变量。

 所以，它的空间复杂度为O(n)

例三：

 来看这个阶乘。

它递归调用了n次。

我们在C语言的函数部分介绍过，函数的每一次递归调用都会为新的函数重新开辟一个栈帧，上一级的函数由于并未结束，所以上一级的函数的栈帧并未被销毁。所以在调用下一级的函数的时候，就不得不在新的位置重新为其开辟栈帧。

所以，它的空间可以理解为开辟了n次。

所以，它的空间复杂度为O(n)。

关于算法的时空复杂度，对于优化代码算法是十分重要的，不过理解起来并没有那么困难。希望读者在理解上述的例题及概念后，可以去牛客网和Leetcode上找一些相应的oj题来练一练。

好啦，有关算法的时空复杂度，我们就探讨到这里啦。

欢迎关注我@jxwd，我将会在将来的2-3个月，持续推出有关数据结构与算法、C++的知识章节，以飨读者。

如果觉着不错，那就不要吝啬你的小手，点个赞吧~~