机器学习2多元元线性回归

---

前言

多元线性回归与一元线性回归操作一样，代入相应公式即可

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、多元函数

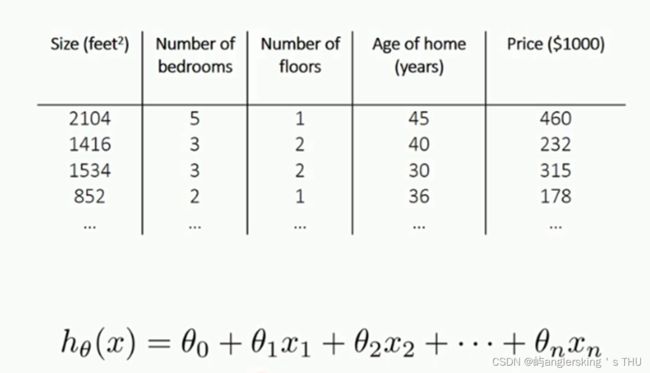
房价预测与为例

二、多元线性函数梯度下降法

求偏导如果比较抽象可看下面一张图

比较具体的公式

二、以房价预测为例实战

数据由房子的大小，年份，决定价格
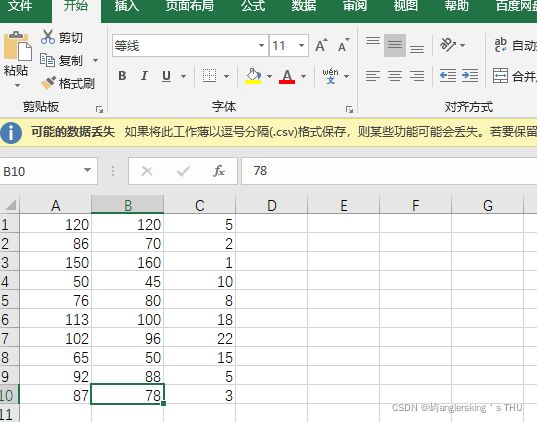
price.csv文件内容

1.代码

代码如下（示例）：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
data = np.genfromtxt('price.csv',delimiter=',')
x_data = data[:,1:3]
y_data = data[:,0]
print(x_data)
print(y_data)
th0 = 0
th1 = 0
th2 = 0
alf = 0.0001
counter = 1000
def costFunc(th0,th1,th2,x_data,y_data):
    totErr = 0
    for i in range(len(x_data)):
        totErr += (th0+th1*x_data[i,0]+th2*x_data[i,1]-y_data[i])**2
    return totErr/float(2*len(x_data))

def gradient_decent(th0,th1,th2,x_data,y_data,alf,counter):

    for i in range(counter):
        th0_temp = 0
        th1_temp = 0
        th2_temp = 0
        for j in range(len(x_data)):
            th0_temp += th0 + th1*x_data[j,0] + th2 * x_data[j,1] - y_data[j]
            th1_temp += (th0 + th1 * x_data[j,0] + th2 * x_data[j,1] - y_data[j])*x_data[j,0]
            th2_temp += (th0 + th1 * x_data[j,0] + th2 * x_data[j,1] - y_data[j])*x_data[j,1]

        m = len(x_data)
        th0 = th0 - alf*(1/m)*th0_temp
        th1 = th1 - alf * (1 / m) * th1_temp
        th2 = th2 - alf * (1 / m) * th2_temp

        print("th0={},th1={},th2={},costErr={}".format(th0,th1,th2,costFunc(th0,th1,th2,x_data,y_data)))
    return th0,th1,th2

th0,th1,th2 = gradient_decent(th0,th1,th2,x_data,y_data,alf,counter)

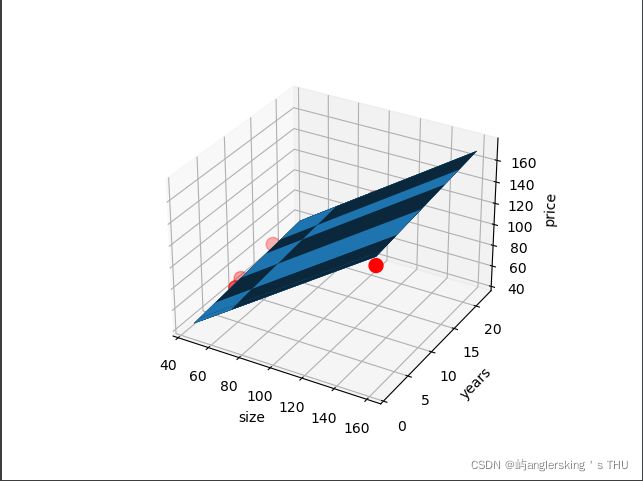
ax = plt.figure().add_subplot(111,projection='3d')
ax.scatter(x_data[:,0],x_data[:,1],y_data,c='r',marker='o',s=100)
x1 = x_data[:,0]
x2 = x_data[:,1]
x1,x2 = np.meshgrid(x1,x2)
z = th0 + th1 * x1  + th2 * x2
ax.plot_surface(x1,x2,z)
ax.set_xlabel('size')
ax.set_ylabel('years')
ax.set_zlabel('price')
plt.show()