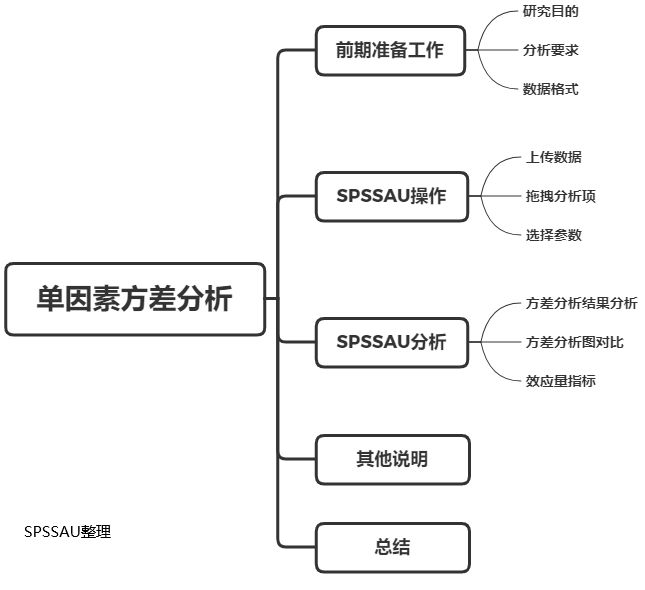
干货。单因素方差分析步骤梳理
方差分析是20世纪20年代发展起来的一种统计方法,它是由英国统计学家费希尔在进行试验设计时为解释试验数据而首先引入的。(来源:统计学 第7版)目前,方差分析广泛应用于生物学、田间试验等。从形式上看,方差分析是比较多个总体的均值是否相等,但本质上是研究变量之间的关系,本篇文章主要介绍单因素方差分析步骤。
一、前期准备
1.研究目的
方差分析(单因素方差分析),用于分析定类数据与定量数据之间的关系情况。例如研究人员想知道三组学生的智商平均值是否有显著差异。方差分析可用于多组数据,比如本科以下,本科,本科以上共三组的差异;而下述t 检验仅可对比两组数据的差异。
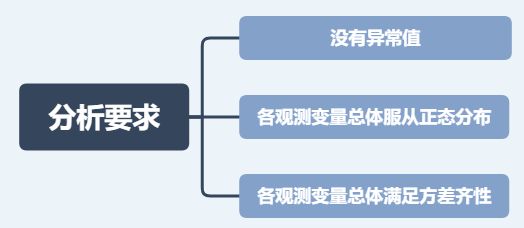
2.分析要求
分析的大致要求如下:
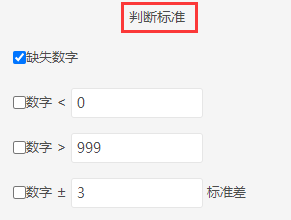
异常值:如果数据有异常值,比如本身数据全部应该大于0,但却出现小于0的数字【可使用SPSSAU通用方法里的频数分析,或者描述分析等进行检查】。可以使用SPSSAU“数据处理”模块下的异常值处理,右侧分析框可以设置“判断标准”
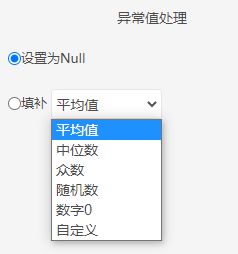
如有异常值,可以对异常值进行处理设为Null或者用平均值、中位数、众数、随机数等进行填补。
正态分布:方差分析理论上是要求数据服从正态分布的,但是理论上的正态分布很难满足,数据接近于正态分布更符合实际情况,因此接近正态分布的数据直接使用方差分析即可,也可以说方差分析对于正态性的要求是稳健的。
方差齐性:一般来讲,方差轻微不齐仅会对方差分析的结论有少许影响。如果方差不齐可以使用其他分析方法,例如:Welch anova、Brown-Forsythe anova。
3.数据格式
方差分析是研究不同组别的差异,比如不同学历时满意度的差异。因此数据格式中一定需要有组别X(比如学历)和分析项Y(比如满意度)。
有时候只有分析项(比如3个分析项),但是现在希望此3个分析项的差异,那么就需要对数据进行改造,自己加入一列‘组别’,然后把数据重叠起来得到分析项Y,类似如下图:
二、SPSSAU操作
1.上传数据
登录账号后进入SPSSAU页面,点击右上角“上传数据”,将处理好的数据进行“点击上传文件”上传即可。
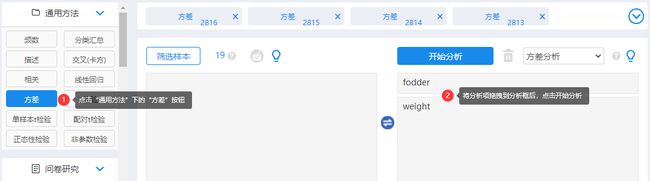
2.拖拽分析项
在“通用方法”模块中选择“方差”方法,将X定类变量放于上方分析框内,Y定量变量放于下方分析框内,点击“开始分析”即可。
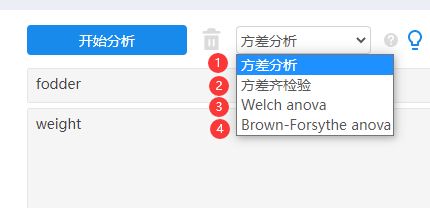
3.选择参数
方差分析方法中有以下4个方法供研究者选择,分别是方差分析、方差齐检验、Welch anova、Brown-Forsythe anova。
方差分析:分析定类数据与定量数据之间的关系情况。
方差齐检验:用于分析不同定类数据组别,对定量数据时的波动情况是否一致。
Welch anova:采用Welch分布的统计量进行的各组均值是否相等的检验
Brown-Forsythe anova:采用Brown-Forsythe分布的统计量进行的各组均值是否相等的检验。
补充说明:如果数据不满足方差齐性也可以使用Welch anova以及Brown-Forsythe anova。
三、SPSSAU分析
1.方差分析结果对比
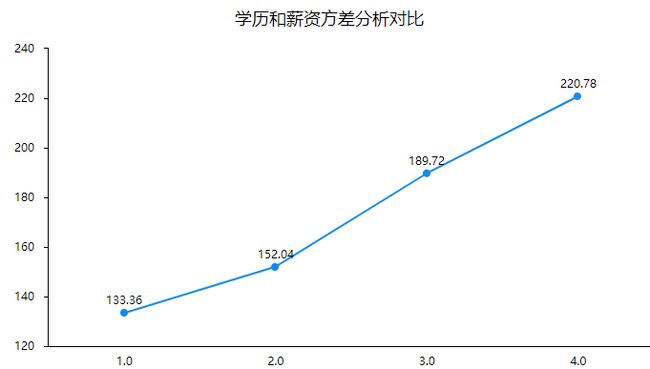
案例背景:分析不同学历之间的工作人员薪资是否有差异。其中1.0代表高中毕业,2.0代表专科,3.0代表本科学历,4.0代表研究生学历(数据只适用于此案例分析)。
学历对于薪资呈现出0.05水平显著性(p=0.000<0.05)同时也可以使用折线图进行直观展示。总结可知:不同学历样本对于薪资全部均呈现出显著性差异。
2.方差分析图对比
上述折线图展示的是学历和薪资方差分析对比,从图中可以看出不同学历样本对于薪资均有着差异性。
3.效应量指标
补充说明:除此之外SPSSAU还提供了方差分析中间过程值表以及方差分析结果的普通格式以及简化纵向格式,如下:
(1)方差分析中间过程值:
(2)方差分析结果(普通格式)
(3)方差分析结果(简化纵向格式)
四、其他说明
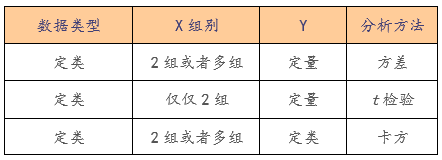
Q1.几种差异性分析
如果X和Y均为定类数据,想对比差异性,此时需要使用卡方分析。如果X为定类,Y为定量;且X分为两组,比如男和女;此时也可使用t 检验进行差异对比(当然也可使用方差分析)。总结如下表:
Q2. 方差分析中间过程值,组间平方和、组内平方和、自由度、均方等问题?
方差分析用于研究差异,差异共由两部分组成,分别是组间平方和,组内平方和;同时对应着自由度值等;计算分别如下:
- 组间自由度df 1=组别数量 – 1;
- 组内自由度df 2 = 样本量 – 组别数量;
- 组间均方 = 组间平方和 / 组间自由度df1;
- 组内均方 = 组内平方和 / 组内自由度df2;
- F 值 = 组间均方 / 组内均方;
- p 值是结合F 值,df 1和df 2计算得到。
五、总结
理论上讲,方差分析前需要满足方差齐,如果方差齐则使用方差分析,如果方差不齐则使用非参数检验。理论和实践相比,永远有gap,现实研究中,最常见的依然是方差分析(而不是非参数检验),原因在于非参数检验的检验效能相对于方差分析会低一些。在方差分析时SPSSAU会自动处理方差齐性问题。
以上就是单因素方差分析步骤的全过程!更多干货登录SPSSAU官网了解更多,进行查看。