[蓝桥杯]2020年第十一届省赛真题C/C++ B组(七月)
文章目录
-
- 试题A: 跑步训练
- 试题B: 纪念日
- 试题C: 合并检测
- 试题D: REPEAT 程序
- 试题E: 矩阵
- 试题F: 整除序列
- 试题G: 解码
- 试题H: 走方格
- 试题I:整数拼接
- 试题 J: 网络分析
试题A: 跑步训练
【问题描述】
小明要做一个跑步训练。
初始时,小明充满体力,体力值计为10000。如果小明跑步,每分钟损耗600 的体力。如果小明休息,每分钟增加300 的体力。体力的损耗和增加都是均匀变化的。
小明打算跑一分钟、休息一分钟、再跑一分钟、再休息一分钟……如此循环。如果某个时刻小明的体力到达0,他就停止锻炼。
请问小明在多久后停止锻炼。为了使答案为整数,请以秒为单位输出答案。
答案中只填写数,不填写单位。
解:以秒为单位输出答案!把每分钟减少或增加的都换成秒为单位的进行计算即可。
#include答案:3880
试题B: 纪念日
【问题描述】
2020 年7 月1 日是中国共产党成立99 周年纪念日。
中国共产党成立于1921 年7 月23 日。
请问从1921 年7 月23 日中午12 时到2020 年7 月1 日中午12 时一共包含多少分钟?
#include答案:52038720
试题C: 合并检测
【问题描述】
新冠疫情由新冠病毒引起,最近在A 国蔓延,为了尽快控制疫情,A 国准
备给大量民众进病毒核酸检测。
然而,由于检测的试剂盒紧缺。
为了解决这一困难,科学家想了一个办法:合并检测。即将从多个人(k个)采集的标本放到同一个试剂盒中进行检测。
如果结果为阴性,则说明这k个人都是阴性,用一个试剂盒完成了k 个人的检测。
如果结果为阳性,则说明至少有一个人为阳性,需要将这k 个人的样本全部重新独立检测(从理论上看,如果检测前k - 1 个人都是阴性可以推断出第k 个人是阳性,但是在实际操作中不会利用此推断,而是将k 个人独立检测),加上最开始的合并检测,一共使用了k + 1 个试剂盒完成了k 个人的检测。
A 国估计被测的民众的感染率大概是1%,呈均匀分布。
请问k 取多少能最节省试剂盒?
思路:
这道题我们先要假设检测的总人数为m,当然你也可以假定一个确定的数字,比如100,1000等等,然后我们根据提意可以得出,检测时先是以k人为单位集体检测,那么我们可以得出首先就需要m/k个试剂盒,并且这个结果是向下取整的,之后这群人中有0.01m个人是阳性的,而且感染是均匀分布的,所以就需要额外的0.01mk个试剂盒(这里就是说把阳性的感染者分成0.01m份,每一份一个人,插入到单位集体中,剩余的其他集体就全部是正常的,所以那0.01m个集体每个人就需要独立的试剂检验,就额外需要0.01m*k份试剂),如果m/k有余的情况,额外的试剂盒还需要加1,所以整个需要的试剂盒就是两者相加。
————————————————
原文链接:https://blog.csdn.net/gwk1234567/article/details/107191352
#include答案:10
试题D: REPEAT 程序
【问题描述】
附件prog.txt 中是一个用某种语言写的程序。
其中REPEAT k 表示一个次数为k 的循环。循环控制的范围由缩进表达,
从次行开始连续的缩进比该行多的(前面的空白更长的)为循环包含的内容。
例如如下片段:
REPEAT 2:
A = A + 4
REPEAT 5:
REPEAT 6:
A = A + 5
A = A + 7
A = A + 8
A = A + 9
该片段中从A = A + 4 所在的行到A = A + 8 所在的行都在第一行的循环两次中。
REPEAT 6: 所在的行到A = A + 7 所在的行都在REPEAT 5: 循环中。
A = A + 5 实际总共的循环次数是2×5×6 = 60 次。
请问该程序执行完毕之后,A 的值是多少?
#include试题E: 矩阵
【问题描述】
把1 ~ 2020 放在2 ×1010 的矩阵里。要求同一行中右边的比左边大,同一列中下边的比上边的大。一共有多少种方案?
答案很大,你只需要给出方案数除以2020 的余数即可。
动态规划:
f[i][j]
集合:所有第一行有 i 个数字,第二行有 j 个数字的方案的集合
属性:数量
决策:
将当前数放在第一行:f[i][j] += f[i - 1][j]
将当前数放在第二行:f[i][j] += f[i][j - 1]
#include试题F: 整除序列
【问题描述】
有一个序列,序列的第一个数是n,后面的每个数是前一个数整除2,请输
出这个序列中值为正数的项。
【输入格式】
输入一行包含一个整数n。
【输出格式】
输出一行,包含多个整数,相邻的整数之间用一个空格分隔,表示答案。
【样例输入】
20
【样例输出】
20 10 5 2 1
【评测用例规模与约定】
对于80% 的评测用例,1 <= n <= 1E9。
对于所有评测用例,1 <= n <= 1E18。
#include试题G: 解码
【问题描述】
小明有一串很长的英文字母,可能包1。
在这串字母中,有很多连续的是重复的。小明想了一个办法将这串字母表达得更短:将连续的几个相同字母写成字母+ 出现次数的形式。
例如,连续的5 个a,即aaaaa,小明可以简写成a5(也可能简写成a4a、aa3a 等)。
对于这个例子:HHHellllloo,小明可以简写成H3el5o2。为了方便表达,小明不会将连续的超过9 个相同的字符写成简写的形式。
现在给出简写后的字符串,请帮助小明还原成原来的串。
【输入格式】
输入一行包含一个字符串。
【输出格式】
输出一个字符串,表示还原后的串。
【样例输入】
H3el5o2
【样例输出】
HHHellllloo
【评测用例规模与约定】
对于所有评测用例,字符串由大小写英文字母和数字组成,长度不超过100。
请注意原来的串长度可能超过100。
#include试题H: 走方格
【问题描述】
在平面上有一些二维的点阵。
这些点的编号就像二维数组的编号一样,从上到下依次为第1 至第n 行,从左到右依次为第1 至第m 列,每一个点可以用行号和列号来表示。
现在有个人站在第1 行第1 列,要走到第n 行第m 列。只能向右或者向下走。
注意,如果行号和列数都是偶数,不能走入这一格中。
问有多少种方案。
【输入格式】
输入一行包含两个整数n, m。
【输出格式】
输出一个整数,表示答案。
【样例输入】
3 4
【样例输出】
2
【样例输入】
6 6
【样例输出】
0
【评测用例规模与约定】
对于所有评测用例,1 <= n <= 30, 1 <= m <= 30。
#include试题I:整数拼接
【题目描述】
给定一个长度为 n 的数组 A1,A2,⋅⋅⋅,An。
你可以从中选出两个数 Ai 和 Aj(i 不等于 j),然后将 Ai 和 Aj 一前一后拼成一个新的整数。
例如 12 和 345 可以拼成 12345 或 34512。
注意交换 Ai 和 Aj 的顺序总是被视为 2 种拼法,即便是 Ai=Aj 时。
请你计算有多少种拼法满足拼出的整数是 K 的倍数。
【输入格式】
第一行包含 2 个整数 n 和 K。
第二行包含 n 个整数 A1,A2,⋅⋅⋅,An。
【输出格式】
一个整数代表答案。
【数据范围】
1≤n≤105,
1≤K≤105,
1≤Ai≤109
【输入样例】
4 2
1 2 3 4
【输出样例】
6
#include试题 J: 网络分析
题目
【问题描述】
小明正在做一个网络实验。他设置了 n 台电脑,称为节点,用于收发和存储数据。初始时,所有节点都是独立的,不存在任何连接。小明可以通过网线将两个节点连接起来,连接后两个节点就可以互相通信了。两个节点如果存在网线连接,称为相邻。小明有时会测试当时的网络,他会在某个节点发送一条信息,信息会发送到每个相邻的节点,之后这些节点又会转发到自己相邻的节点,直到所有直接或间接相邻的节点都收到了信息。所有发送和接收的节点都会将信息存储下来。一条信息只存储一次。给出小明连接和测试的过程,请计算出每个节点存储信息的大小。
【输入格式】
输入的第一行包含两个整数 n, m,分别表示节点数量和操作数量。节点从1 至 n 编号。接下来 m 行,每行三个整数,表示一个操作。如果操作为 1 a b,表示将节点 a 和节点 b 通过网线连接起来。当 a = b时,表示连接了一个自环,对网络没有实质影响。如果操作为 2 p t,表示在节点 p 上发送一条大小为 t 的信息。
【输出格式】
输出一行,包含 n 个整数,相邻整数之间用一个空格分割,依次表示进行
完上述操作后节点 1 至节点 n 上存储信息的大小。
【样例输入】
4 8
1 1 2
2 1 10
2 3 5
1 4 1
2 2 2
1 1 2
1 2 4
2 2 1
【样例输出】
13 13 5 3
#include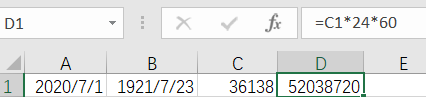
![[蓝桥杯]2020年第十一届省赛真题C/C++ B组(七月)_第1张图片](http://img.e-com-net.com/image/info8/ddbd2c1bddbe47958c1c438f97752b4f.jpg)