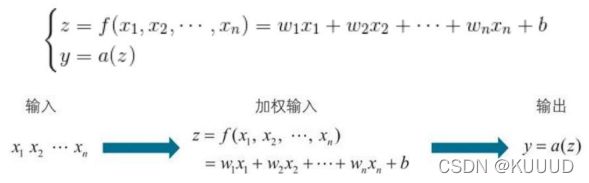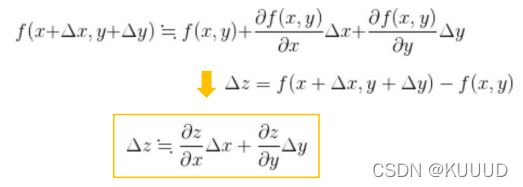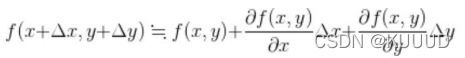掌握神经网络的法宝（一）

目录

系列文章目录

前言

 一、误差反向传播法所需的链式法则

二、梯度下降法的含义与公式（附代码）

三、最优化问题和回归分析（附代码）

总结

---

系列文章目录

第一章：会思考的机器你造嘛——AI技术

​第二章：深度学习敲门砖——神经网络 ​

第三章：掌握神经网络的法宝（一）

---

前言

        通过上一章的介绍，相信大家对于神经网络的框架模式有了一定的了解，而这一章我准备来给大家介绍一下掌握神经网络所需的数学基础。神经网络用到的算法就是向量乘法，并且广泛采用符号函数及其各种逼近。并行、容错、可以硬件实现以及自我学习特性，是神经网络的几个基本优点，也是神经网络计算方法与传统方法的区别所在。

---

 一、误差反向传播法所需的链式法则

1.1神经网络和复合函数

        已知函数y = f(u)， 当u = g(x)时，y作为x的函数库也表示为形如y = f(g(x))的嵌套结构（u和x都表示多变量）。这时，嵌套结构的函数f(g(x))称为f(u)和g(x)的复合函数。

        就如我们上一章所讲到的神经单元的激活函数：y = a(w1x1+w2x2+···+wnxn+b),其中w1,w2···,wn作为各输入的权重，b为神经单元的偏置，n为输入的个数。这个输出函数是如下x1,x2,···,xn的一次函数f 和激活函数a 的复合函数：

1.2 单变量函数的链式法则

        1）已知单变量函数y = f(u)，当u表示单变量函数u = g(x)，复合函数f(g(x))的导函数可以如下简单地求出来：

        2）单变量函数的近似法则：

1.3 多变量函数的链式法则 

        1）变量z为u，v的函数，如果u，v分别为x，y的函数，则z为x，y的函数，此时下式（多变量的链式法则）成立：

        2）多变量函数的近似法则

1.4 近似法则的总结和扩展

        近似法则的向量表示：

---

二、梯度下降法的含义与公式（附代码）

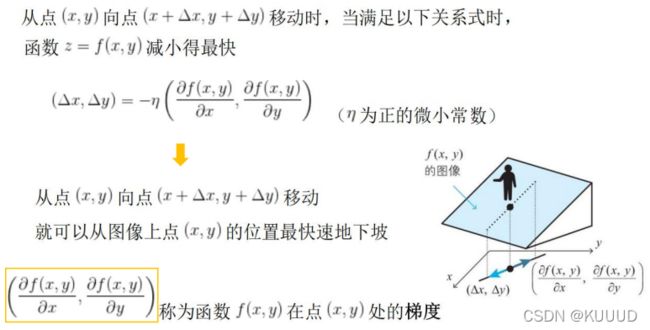
2.1 梯度下降法的思路

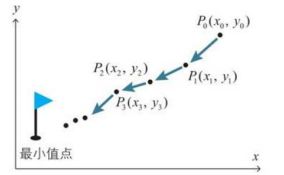
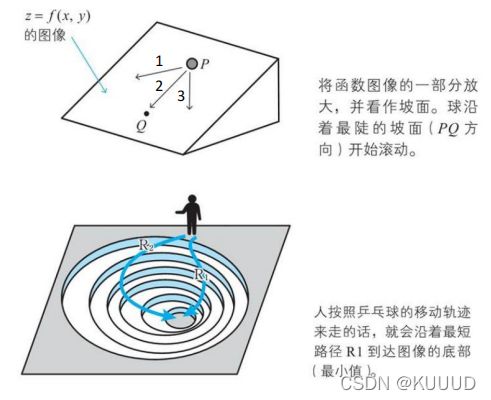
        梯度下降法不直接求解上式的方程，而是通过慢慢地移动图像上的点进行摸索，从而找出函数的最小值：

 下面给大家一个例子让大家好理解一下：

2.2 近似公式和内积的关系

        套用多变量函数的公式：

        可以递推为以下模式：

2.3 向量内积的回顾

2.4 二变量函数的梯度下降法的基本式 

2.5 将梯度下降法推广到三个变量之上的情况

2.6 学习率的含义以及梯度下降法的要点

1）所谓梯度下降法，就是分别求损失函数对各个参数的偏导数，然后乘以一个系数η，把它作为参数的更新量。这个参数η，就称为学习率。

        学习率的选择非常重要，η在梯度下降法中也叫作步长，通过控制η来控制每一步的距离：    

• 如果η 过小，计算较慢，需要迭代多次；
• 如果η 过大，参数就可能在迭代的过程中“越过”最低点，来回震荡，甚至无法收敛；

2）梯度下降法的要点：

• 不同的起始点，可能导致最后得到的局部最小值点不同。
• 每次迭代的时候，我们需要同时更新，直至所要的式子收敛，这就是梯度下降法的核心。

2.7 梯度下降法python举例 

from random import random

def gradient_decent(fn, partial_derivatives, n_variables, lr=0.1, max_iter=10000, tolerance = -5):
    theta = [random() for _ in range(n_variables)]
    y_cur = fn(*theta)
    for i in range(max_iter):
        #calculate gradient ofcurrent theta
        gradient = [f(*theta) for f in partial_derivatives]
        #updata the theta bythe gradient
        for j in range(n_variables):
            theta[j] -= gradient[j]*lr
        #cheak if converged or not
        y_cur, y_pre = fn(*theta), y_cur
        if abs(y_pre-y_cur) < tolerance:
            break
    return theta, y_cur

def f(x, y):
    return (x+y-3)**2 + (x+2*y-5)**2+2
def df_dx(x, y):
    return 2*(x+y-3) + 2*(x+2*y-5)
def df_dy(x, y):
    return 2*(x+y-3) + 4*(x+2*y-5)

if __name__ == '__main__':
    print("Solve the mininum value of quadratic function:")
    n_variables = 2
    theta, f_theta = gradient_decent(f, [df_dx, df_dy], n_variables)
    tehta = [round(x, 3) for x in theta]
    print("The solution is: theta %s, f(theta) %.2f.\n" % (theta, f_theta))

运行结果：

三、最优化问题和回归分析（附代码）

3.1 最优化问题

        在为了分析数据而建立数学模型时，通常模型是由参数确定的。在数学世界中，最优化问题就是如何确定这些参数的。

        而且从数学上来说，确定神经网络的参数是一个最优化问题，具体就是对神经网络的参数（即权重和偏置）进行拟合，使得神经网络的输出与实际数据相吻合。

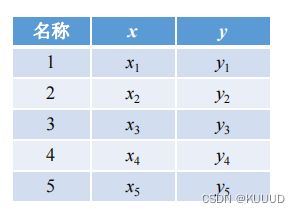
3.2 回归分析

        由多个变量组成的数据中，着眼于其中一个特定的变量，用其余的变量来届时这个特定的变量，这样的方法称为回归分析。

3.3 代价函数

• 在最优化方面，误差总和可以称为“误差函数”、“损失函数”、“代价函数”等；
• 除了平方误差的总和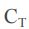之外，代价函数还存在其他多种形式；
• 利用平方误差的总和进行最优化的方法称为最小二乘法。

3.4  最小二乘法的python举例

import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
import scipy.optimize as opt
from scipy import sparse
import numpy as np

#拟合函数
def func(a, x):
    k, b = a
    return k*x+b

def dist(a, x, y):
    return func(a, x) - y

font = FontProperties()

plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['font.sans-serif'] = 'Droid Sans Fallback'
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False

plt.figure()
plt.title(u'女生的身高体重数据')
plt.xlabel(u'体重/kg')
plt.ylabel(u'身高/cm')
plt.axis([40, 80, 140, 200])
plt.grid(True)
x = np.array([48.0, 57.0, 50.0, 54.0, 64.0, 61.0, 43.0, 59.0])
y = np.array([165.0, 165.0, 157.0, 170.0, 175.0, 165.0, 155.0, 170.0])
plt.plot(x, y, 'k.')
param = [0, 0]
var = opt.leastsq(dist, param, args = (x, y))
k, b = var[0]
print(k, b)
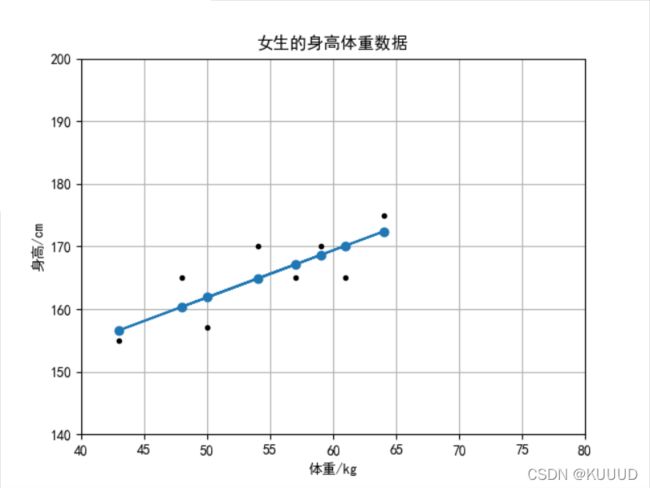
plt.plot(x, k*x+b, 'o-')
plt.show()

 拟合出来的结果：k = 0.7514124562779751; b = 124.29802113285037;

 

3.5 模型参数的个数

• 回归方程是根据大量的条件所得到的折中结果；

• 要确定模型，就必须准备好规模大于参数个数的数据；

---

总结

        以上就是今天要讲的内容，本文介绍了神经网络所需的数学基础，误差反向传播法所需的链式法则、梯度下降法的含义与公式以及最优化问题和回归分析的相关知识。

        欢迎大家留言一起讨论问题~~~