李宏毅2021春机器学习课程笔记——Introduction of Machine/Deep Learning
本文作为自己学习李宏毅老师2021春机器学习课程所做笔记,记录自己身为入门阶段小白的学习理解,如果错漏、建议,还请各位博友不吝指教,感谢!!
一、Machine Learning概念理解

Machine Learning主要的任务是寻找一个合适的Function来完成我们的工作(非常不严谨的简单理解),如上图中的Image Recognition,就是要寻找一个合适的 f f f,实现通过对输入的图片进行各种转换识别出图片中的事物是一只猫的功能。
二、Different types of Functions
- Regression: The function outputs a scales(连续的数值).
例如:预测PM2.5
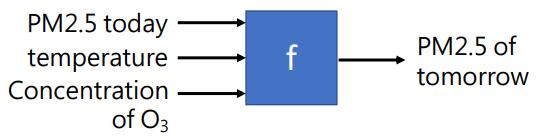
输入:今天的PM2.5数值、温度、 O 3 O_3 O3的浓度
Function: f f f实现对PM2.5数值的预测功能
输出:明天的PM2.5数值 - Classification:Given options(classes), the function outputs the correct one.
例如:垃圾邮件分类

输入:邮件内容
Function:事先给出类别(是垃圾邮件,不是垃圾邮件), f f f实现根据输入的邮件内容,对该邮件进行分类的功能
输出:输入邮件的类别 - Structured Learning and more
三、How to find the function?
以预测YouTube视屏播放量为例:
1. 根据专业知识构建Model
| model | y = b + w x 1 y = b + wx_1 y=b+wx1 |
| 输入:特征(feature) x 1 x_1 x1 | 为2/25的播放量 |
| 输出: y y y | 为2/26的播放量 |
| weight w | f f f要学习的参数 |
| bias b | f f f要学习的参数 |
2. 结合训练数据定义损失函数(Loss Function)
定义损失函数的目的是使用损失函数来评价Model效果的好坏,而需要Model: y = b + w x 1 y=b+wx_1 y=b+wx1自己学习的参数是 w w w和 b b b(也就是weight和bias决定了Model的预测效果)。所以Loss Function是关于 w w w和 b b b的Function,以此来评价Model的效果。
通常来说,Loss Function的值越大(损失越大),Model效果越差;Loss Function的值越小(损失越小),Model的效果越好。常见的Loss Function有如下几种:
- mean absolute error(MAE): e = ∣ y − y ^ ∣ e = |y-\hat{y}| e=∣y−y^∣
- mean square error(MSE): e = ( y − y ^ ) 2 e = (y-\hat{y})^2 e=(y−y^)2
包括损失函数的适用性有待继续补充……
3. 优化参数
此处使用随机梯度下降算法进行优化,获得让Loss Function值最小的 w w w和 b b b。优化过程如下:
-
(随机)初始化Model的参数 w 0 w^0 w0, b 0 b^0 b0
-
计算各个参数的梯度:
∂ L ∂ w ∣ w = w 0 , b = b 0 \frac{\partial L}{\partial w}|_{w=w^0,b=b^0} ∂w∂L∣w=w0,b=b0
∂ L ∂ b ∣ w = w 0 , b = b 0 \frac{\partial L}{\partial b}|_{w=w^0,b=b^0} ∂b∂L∣w=w0,b=b0
-
分别更新参数 w w w和 b b b
w 1 ← w 0 − η ∂ L ∂ w ∣ w = w 0 , b = b 0 w^1 \leftarrow w^0 - \eta\frac{\partial L}{\partial w}|_{w=w^0, b=b^0} w1←w0−η∂w∂L∣w=w0,b=b0
b 1 ← b 0 − η ∂ L ∂ b ∣ w = w 0 , b = b 0 b^1 \leftarrow b^0 - \eta\frac{\partial L}{\partial b}|_{w=w^0, b=b^0} b1←b0−η∂b∂L∣w=w0,b=b0
其中 η \eta η为学习率,是自己手动设置的一个参数。(所有需要自己手动设置的参数都称为“超参数”)
-
直到获得 w ∗ w^* w∗和 b ∗ b^* b∗使得 w ∗ , b ∗ = a r g min w , b L w^*,b^* = arg\, \min_{w,b}L w∗,b∗=argminw,bL
四、深度学习引入
在第三部分中,所构建的模型 y = b + w x 1 y=b+wx_1 y=b+wx1,是简单的Linear model,如果遇到很复杂的情况,简单的Linear model是无法表示的,这种限制被称为Model Bias。

如上图所示,红线表示真实的数据,蓝线表示Linear Model。三条蓝线代表权重 w w w和 b b b不同的model,可以看出无论 w w w和 b b b怎样变化,Linear model都无法很好的表示红线代表的情况,这就是Model Bias。
我们可以构建更加复杂灵活的模型来解决Model Bias问题:
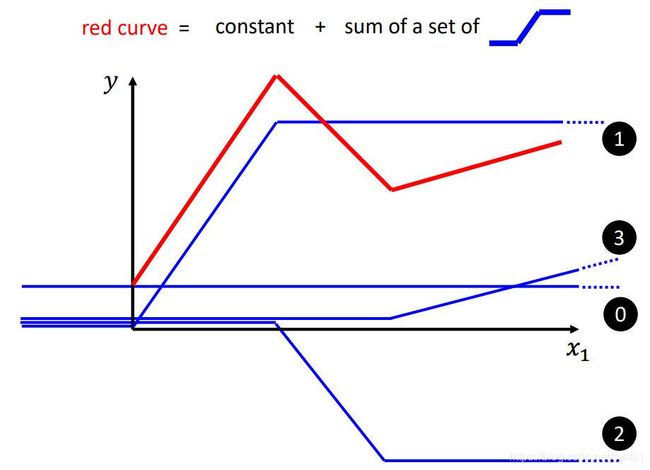
如上图所示,我们可以使用一组蓝线相加,来构建模型表示红线。从左到右:
- 第一段斜率大于0的红线,可以使用1号蓝线来表示
- 中间斜率小于0的红线,可以使用2号蓝线来表示
- 第二段斜率大于0的红线,可以使用3号蓝线来表示
- 最后将将1,2,3号蓝线相加,在加上一个表示红线与y轴交点的constant来拟合红线。即:red curve = constant + sum of a set of blue curve
通过这种方式,只要我们使用足够多的蓝线,是可以构建出一个能很好的表示出真实曲线(红色曲线)的model的。
构建模型
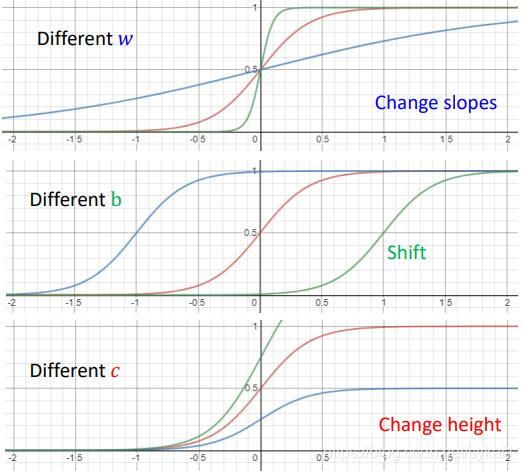
在应用过程中我们可以选择sigmoid函数来作为蓝线构建model(当然也可以选择其他的函数,此处仅作举例表示)。
Sigmoid Function:
y = c 1 1 + e − ( b + w x 1 ) = c s i g m o i d ( b + w x 1 ) \begin{aligned} y &= c\frac{1}{1+e^-(b+wx_1)} \\ &= c sigmoid(b+wx_1) \end{aligned} y=c1+e−(b+wx1)1=csigmoid(b+wx1)
函数图像如下所示:
如下图所示,使用sigmoid函数,按照上边的步骤来表示真实情况:

当只有一个特征 x 1 x_1 x1时,可以得到model:
y = b + ∑ i c i s i g m o i d ( b i + w i x 1 ) y = b + \sum_{i}c_isigmoid(b_i+w_ix_1) y=b+i∑cisigmoid(bi+wix1)
当有多个特征 x j x_j xj时,可以得到model:
y = b + ∑ i c i s i g m o i d ( b i + ∑ j w i j x j ) y = b + \sum_{i}c_isigmoid(b_i+\sum_{j}w_{ij}x_j) y=b+i∑cisigmoid(bi+j∑wijxj)
为了有直观的理解,假设i:1,2,3; j:1,2,3,并画出图来,如下所示:
- b i + ∑ j w i j x j b_i + \sum_{j}w_{ij}x_j bi+∑jwijxj画图表示如下:
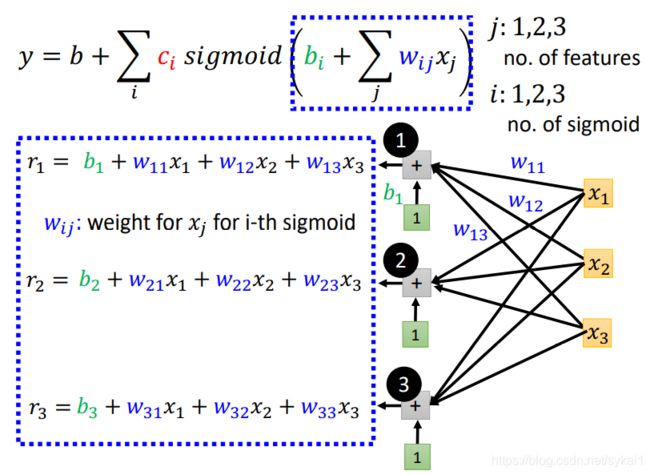
使用矩阵表示作进一步简化:

- s i g m o i d ( b i + ∑ j w i j x j ) sigmoid(b_i+\sum_{j}w_{ij}x_j) sigmoid(bi+∑jwijxj)画图表示如下:

- b + ∑ i c i s i g m o i d ( b i + ∑ j w i j x j ) b+\sum_{i}c_isigmoid(b_i+\sum_{j}w_{ij}x_j) b+∑icisigmoid(bi+∑jwijxj)画图表示如下:
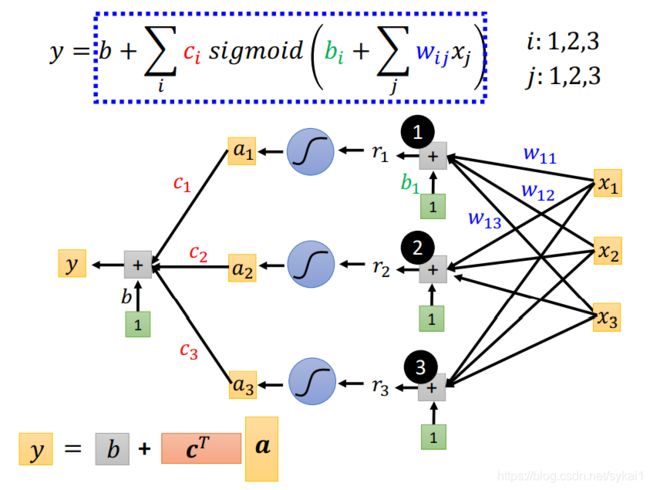
到此为止就构建了一个简单的神经网络。
定义Loss Function
在第三步中介绍到,完成model的构建的下一步是定义Loss Function。Loss Function是关于model中未知参数的Function,在这里的未知的参数有 W , b , b , c T W,b,\mathsf{b},c^{T} W,b,b,cT。

如上图所示,我们将这些参数合并成一个 θ \theta θ向量,定义损失函数 L ( θ ) L(\theta) L(θ)如下:
L ( θ ) = 1 N ∑ n e n = 1 N ∑ n ( y ^ − y ) = 1 N ∑ n ( y ^ − ( b ′ + c T σ ( b + W x ) ) ) \begin{aligned} L(\theta) &= \frac{1}{N}\sum_{n}e_n \\ &=\frac{1}{N}\sum_{n}(\hat{y}-y) \\ &=\frac{1}{N}\sum_{n}(\hat{y}-(b^{'}+c^T\sigma(b+Wx))) \end{aligned} L(θ)=N1n∑en=N1n∑(y^−y)=N1n∑(y^−(b′+cTσ(b+Wx)))
优化参数
在深度学习中,往往将训练数据集随机划分为N个batch,每完成一个batch的计算,便更新一次参数 θ \theta θ,一轮(epoch)完成对所有N个batch的计算。

五、总结
- 机器学习粗浅理解:寻找一个 f f f,通过输入训练数据 x x x,来训练 f f f中的未知参数,使得 L ( θ ) L(\theta) L(θ)最小,来完成我们的工作。
- 对于机器学习任务的分类有如下几个:
- Classification(分类任务)
- Regression(回归任务)
- Structured Learning(结构学习)
……
- 构建模型的步骤:
- 根据专业知识构建model。
- 结合数据定义损失函数 L ( θ ) L(\theta) L(θ)
- 优化参数 θ \theta θ直到获得 θ ∗ = a r g m i n θ L ( θ ) \theta^* = arg min_{\theta}L(\theta) θ∗=argminθL(θ)
- 一些需要理解的概念
- 超参数(hyperparameter):模型中需要自己手动设置的参数。
- Model Bias:指模型不能很好的表示真实情况的限制。
- batch & epoch
- sigmoid function: y = c 1 1 + e − ( b + w x ) y=c\frac{1}{1+e^{-(b+wx)}} y=c1+e−(b+wx)1,relu function: y = c m a x ( 0 , b + w x ) y=c max(0,b+wx) y=cmax(0,b+wx)