元学习方向 optimization based meta learning 之 MAML论文详细解读

元学习系列文章

1. optimization based meta-learning
   1. 《Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks》 论文翻译笔记
   2. 元学习方向 optimization based meta learning 之 MAML论文详细解读：本篇博客
   3. MAML 源代码解释说明 (一)
   4. MAML 源代码解释说明 (二)
   5. 元学习之《On First-Order Meta-Learning Algorithms》论文详细解读
   6. 元学习之《OPTIMIZATION AS A MODEL FOR FEW-SHOT LEARNING》论文详细解读
2. metric based meta-learning: 待更新…
3. model based meta-learning: 待更新…

目前 meta-learning 的研究一共有三个方向：

1. optimization based
2. metric based
3. model based

本篇要讲的论文是第一个方向，optimization based 中的开篇之作，《Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks》 简称 MAML

引言

上一篇博客是对这篇论文的纯翻译，这次来讲解下这篇论文是怎么做 meta-learning 的，这篇论文是 2017 年发表在 ICML 会议的，算是 optimization based 这个方向的开篇之作，后续的一些文章都有借鉴此论文的 idea。而且这篇论文的思想很简单，但是看明白后会惊讶于作者的思想是如此神奇，简单之中蕴含着大道理。

相关概念

meta learning

meta learning 俗称元学习，目标是 learn to learn，即学会如何学习。听起来有点绕，大白话解释就是通过之前任务的学习使得模型具备一些先验知识或学习技巧，从而在面对新任务的学习时，不至于一无所知。这更接近于人的学习过程，我们人在过去的经历中，会不断地积累学习经验，使自己的知识积累变得越来越丰富，所以在面对新问题的时候，并不是一无所知的，可以自动借鉴之前相似问题的经验来解决新问题。所以元学习也被称为是机器实现通用人工智能的关键技术。

meta-learning 学习的对象是 Tasks，而不是 Samples 样本点，因为 meta-learning 最终要解决的问题是在新的 task 上可以更好的学习，所以要迁移之前 task 上的学习经验。那么在训练阶段，输入的就是不同的 tasks，如下图所示，所有的 task 都是五分类任务，每个 task 仍然有训练集和测试集，训练集是 5 类不同的图片，该 task 的测试集是这 5 类中没有出现过的样本。不同的 task 对应的 5 个类别是不一样的，那么在若干个这样的 task 上训练之后，需要在一个新的任务上进行 meta 的测试/推理，测试任务是从未见过的 5 个类别的样本，让模型在这些样本上进行微调的训练，只不过这时候的模型在训练时就已经具备了之前学习到的 “经验”，从而可以快速适应测试任务。

transfer learning

transfer learning 迁移学习，同样也是迁移之前学习到的 “经验”，在新的数据上进行微调，比如用在 ImageNet 大数据集上预训练的 VGG 等模型，在自己的图片数据集上微调 VGG 进行特征提取，不过这里和 meta-learning 有本质的区别，稍后会详细说明。

multi-task learning

multi-task learning 是多任务学习，多个任务一起进行训练，以达到相互辅助训练的作用，这里的多任务可以是同一数据多个目标任务，也可以是多个数据同一个目标任务，如在人脸识别数据集上，既进行人脸识别任务，又要预测出该人脸的性别和年龄等。

few shot learning

few shot learning 少样本学习，是指一份数据中可用来训练的样本很少，比如只有 10 条或者 5 条样本，那么这时候用常规的训练方式，是学不出什么的，因为可用信息太少了，那么自然就会想到用 meta-learning 的方式来训练，借助之前任务的先验经验来学习少样本的任务。few shot learning 可以说是 meta learning 在监督学习中的一个典型应用，而 meta-learning 个人觉得是一个思想框架，可以用在少样本数据上也可以用在多样本数据上，只不过在 few-shot 的场景下，更能发挥出它的威力。比如一个10条样本的分类数据，用普通的训练方式，可能只取得 10% 的准确率，但用 meta-learning 的方式训练可以取得 70% 的准确率。 样本数量比较多的时候，用普通的训练方式就可以取得不错的效果，比如准确率 95%，用 meta-learning 的方式可能取得 97% 的准确率，但预训练过程就比较麻烦了。

few shot learning 中还有两个比较特殊的场景，就是 one shot 和 zero shot，即只有1个样本，甚至是零训练样本的场景，不过不在这次的讨论范围之内，如果大家比较感兴趣可以自行查找这方面的论文，few shot learning 目前也是学术上的研究热点。

optimization based meta-learning

文章开头提到 meta-learning 的研究共有三个方向，第一个方向就是 optimization based meta-learning，而 MAML 是这个方向的开山之作，所以要想知道 MAML 是怎么做的，首先要知道这个方向是如何实现 metalearning 的。

思考一下，我们平时普通 learn 的模式是怎样训练模型的？以 DNN 网络模型为例，首先是搭建一个网络模型，接着对模型中每层的参数进行初始化，然后不断的进行“前向计算 loss -> 反向传播更新参数”的过程，直到 loss 收敛。这个过程中，模型初始时对当前数据是一无所知的，所以要通过随机初始化的方式对参数进行赋值，尽管用多种初始化方式，但总归都是随机的。那么有没有方法可以让模型从一个给定的位置开始训练呢，并且这个初始位置给的好的话，比如就在全局最优解附近，可能只需要迭代几次模型就收敛了。答案是肯定的，这个方向的 metaleaning 就是来做这个事情的。简单总结下就是 optimization based meta-learning 是通过之前大量的相似任务的学习，给网络模型学习到一组不错的/有潜力的/比较万金油的参数，使用这组参数作为初始值，在特定任务上进行训练，只需要微调几次就可以在当前的新任务上收敛了，这句话有几个值得注意的地方或者使用要求：

1. 相似任务：并不是随便找一个数据就可以拿来进行训练。
2. 共用一个网络模型：我们的最终目的是使用 DNN 模型在任务 A 上进行训练，为了避免随机初始化的方式，故而采用 metalearning 方式，对这个 DNN 模型先进行预训练，这个预训练的过程就是 meta 训练，其结果是得到一组不错的 DNN 参数，然后在任务A上进行微调。所以从始至终，就只有一个相同的 DNN 模型。
3. 特定任务：这个特定任务是我们实际关心的任务，也是 meta 的推理任务，所以要和 meta 训练阶段的大量任务具有一定的相似性，如果差异性太大，那么 meta 学到的这组参数可能不起作用甚至还不如随机初始化的参数。

乍一看是不是觉得和迁移学习有点像，最终形式都是从一组已知参数开始微调，但是这两个方式是有本质的区别的，这个后面还会再讲到。

一个形象化例子

在开始讲论文之前，先来看一个形象化的例子，这个例子是楼主骑车的时候无意中想到的，和论文的思想很像。这个例子就是老师教学生学习的过程，场景设定是有一个刚开始时对世界一无所知的学生，这个学生希望通过不断的学习，具备一定的学习技巧或经验，从而可以在新的没有见过的科目上，只需要简单的学习几天，就可以在该科目上考出好成绩。为了达到这个目的，该学生请了一个老师，老师为了训练学生的学习能力，让这个学生同时学习不同的科目，比如语文、数学、英语等，然后每个科目都学习七天，七天之后进行各科的考试，老师会计算出该学生的平均考试成绩，并根据这次的平均成绩，对该学生的学习做出相应的指导，比如调整学习路线或者告诉他一些学习技巧等；然后让这个学生再次学习七天并考试一次，老师还是根据平均成绩进行指导，如此不断地执行这个过程，直到老师觉得该学生的考试成绩达标了，比如最近几次的平均成绩都可以到 90 分以上，就停止对这个学生的训练，并认为此时的学生已经具备了很好的学习能力。那么如何检验该学生的学习能力呢？方式就是找一个未曾学过的科目，比如操作系统，让这个学生从零开始学起，七天之后来考试一次，看他在操作系统这门课上的考试成绩如何，如果成绩很好，说明该学生已经具备了很强的学习能力，当然不一定是学习七天就考试，也可以学习一个月或者更久再进行考试。

这个例子中有两个需要思考的问题：

1. 老师训练期间，如何衡量学生当前学的好不好？
2. 老师训练期间，如何衡量学生学习能力强不强？

很明显，学的好不好就是通过当前科目上的考试成绩来判断，学习能力强不强，则是通过学习时间来判断，比如学习七天考到90分和学习一天就考到90分，是两种不同的学习能力。

MAML

论文标题

重头戏来了，先来解读下论文标题：Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks，这个标题中透漏出三个信息：

1. 模型无关：模型无关不是说任意模型都行，这个范围太广了，是指任意的可以通过梯度下降进行优化训练的模型，这个模型一般都是网络模型，也可以是支持随机梯度下降的机器学习模型。
2. 快速适应：意思是模型经过较少的迭代次数就可以在当前任务上收敛
3. 多场景：论文的方法可以适用到分类、回归、强化学习等场景

算法流程

下图是论文中的伪算法，这里以监督学习中少样本分类场景为例，整体思想都是一样的。

先来解释下这个伪算法：

• 第一个 Require 很关键，也往往容易忽略，就是要求所有的任务都服从一个分布 P(T)，每个任务是从这个分布中采样得到的。这就说明了不能随意拿一个 Task 放到 MAML 框架里，必须满足某种相似性。
• 第二个 Require，这两个是模型超参数，我们的设置是，有一个用于多分类的网络模型 DNN，现在要通过元学习的方式得到网络模型的一组初始参数，为了得到这组参数，MAML 设计了两层训练，一个是 Task 内部的训练更新，更新的学习率是 α，一个是外部的网络模型的训练更新，更新的学习率是 β。可以把内部任务的训练，想象成前面例子中学生在每个科目上的学习过程，而外部的更新，则是老师调整学生学习方向的过程。

1. 训练前首要先随机初始化网络模型所有参数 $\theta$
2. 设置一个外层训练结束条件，例如迭代 10000 步等
3. 外层训练就是 Meta 训练过程，上面讲过 Meta 训练的对象是 task，所以 meta 每一次的迭代都要从任务分布 p(T) 中随机抽取一个 batch 的 tasks
4. 针对 3 中的每个 task，执行下面的过程：
5. 在一个具体的任务 Ti 中随机抽取包含 K 个数据点的训练样本集 D
6. 使用交叉熵损失函数或者均方差损失函数，在 D 上计算出损失函数 $L_{t_i}$和损失函数对 θ 的梯度
7. 使用 6 计算出的梯度，在该任务上使用一次梯度下降更新模型参数 θ：${\theta }_i^{\prime }=\theta -\alpha ⊽$
8. 从该任务 Ti 中抽样出一个测试集 D’，用于 meta 的参数更新
9. 每个 task 都执行 6,7,8 三步，直到这一个 batch 的 task 都执行完
10. 这一步就是 meta 的更新过程， 虽然 7 也有更新模型参数，但是那是任务内的局部更新，并没有改变外面网络模型的参数，这一步就是要改变网络模型的参数了，仍然是使用梯度下降法进行更新，只不过更新用到的梯度是每个任务 Ti 在各自的测试集 D’ 上计算出的batch 个梯度的平均梯度，更新的步长是 β。可以把这一步的更新，想象成上面例子中老师根据学生的平均考试成绩来调整其学习方向的过程，考试题目自然是各科上没见过的题目，这也就是第 8 步抽取测试集 D’ 的作用，然后每个任务用自己更新过的模型参数 ${\theta }_i^{\prime }$ 在 $D^{\prime }$ 上进行前向计算得到一个 loss，用这个 loss 再对 ${\theta }_i^{\prime }$ 进行求导得到测试集 $D^{\prime }$ 上的梯度，这个梯度就相当于是该任务上的考试成绩

上面的过程中有一个问题需要事先说明：可以看到每个任务内部只更新了一次参数，也就是 6,7 两步只做了一次梯度更新，但其实也可以进行多次的梯度更新，就是把 6,7 两步重复执行几次。那作者这里为什么只写一次呢？这就是作者高明的地方了，那就是做了一个最大化假设。我们的最终目的是希望 MAML 训练出的参数，在新的任务上进行少量几次的微调就可以收敛，那最好的结果就是只更新一次就收敛了，所以在 MAML 训练过程中，作者就特意设计每个任务内部只更新一次参数，以此来训练这个模型 “更新一次就可以最大化性能”的能力。类比到上面讲的例子，那就是老师希望该学生具备强大的学习能力，在新的没有见过的科目上只学习一天就可以考出好成绩，为了训练该学生的这个能力，就让他在训练的每个科目上都学习一天然后考试一次，老师根据平均考试成绩调整学生的学习方向，不断地重复这个过程，直到平均考试成绩可以到 90 分以上就结束训练，此时老师就认为这个学生具备了“在新科目上学习一天就能考出好成绩”的能力。

基于上面的分析，楼主自己画了一个流程图来表示通用 MAML 的训练更新过程：

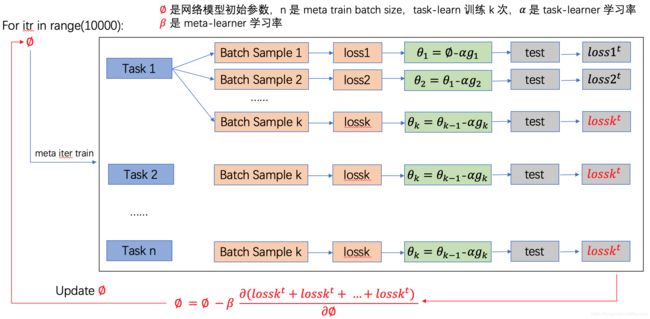
这个图中是以 task 内部更新 k 次参数为例的，k=1 的时候就和 MAML 一模一样了。

Warning of Math

下面到了一个容易犯困的环节，伟大的思想背后自然要有坚实的数学理论支撑，MAML 的数学过程就是其训练更新的过程，理解了数学过程才能更好的理解 MAML 的思想。不过在论文中，并没有过多的的数学过程介绍，可能是作者觉得太简单了吧，下面的数学过程也是楼主参考一些资料总结出的。

上图是 MAML 训练时模型参数的更新过程，其中 $\varphi$ 是网络模型的初始参数，也就是伪算法中的 1 那一步，${\hat{\theta }}^{\prime }$ 是任务内部在 $\varphi$上更新一次后的参数，也就是伪算法的第 7 步，$L(\varphi )$是所有 task 在各自测试集 $D^{\prime }$ 上的 loss 和，用 $L(\varphi )$对模型参数$\varphi$进行求导得出梯度，来进行meta的参数更新，也就是真正更新网络模型的参数。图中右边的过程就是把 meta 梯度下降更新的数学过程展开，其中最关键的一步是蓝色弯箭头标出的那个变换，就是第二个等号到第三个等号的那一步，其它步骤还都比较好理解，下面来详细看下关键这步的变换，其中主要是 $l({\theta }^{\prime })$对 $\varphi$求导不好求，如果这个可以算出来，剩下的步骤就好说了。

上图就是计算 $l({\theta }^{\prime })$对 $\varphi$求导的过程，因为${\theta }^{\prime }$是由$\varphi$经过一次梯度下降更新得到的, $\varphi$其实是一组参数向量，代表网络模型的各个参数，所以可以将求导展开成向量形式，向量每个元素是 $l({\theta }^{\prime })$对 ${\varphi }_i$的求导，也就是上图中的红框1，那如何计算$l({\theta }^{\prime })$对 ${\varphi }_i$的求导呢？我们知道${\theta }^{\prime }$是由 $\varphi$经过梯度下降公式得到的，那么 ${\varphi }_i$和${\theta }^{\prime }$的关系就是下面这样：

也就是 ${\varphi }_i$和每个 ${\theta }_j$都是有关系的，${\hat{\theta }}^{\prime }$又是由多个 ${\theta }_j$组成的，所以 $l(\theta )$对${\varphi }_i$的求导就是对上面的链路求导的和，每个路径的求导则是$l(\theta )$对${\theta }_j$求导结果和${\theta }_j$$对{\varphi }_i$的求导结果相乘，也就是上图中红框2所在的公式，其中的关键是红框2的位置，也就是 ${\theta }_j$$对{\varphi }_i$的求导，${\theta }_j$$是{\varphi }_j$经过梯度下降公式变过来的，也就是图中的红色5标记的地方， 所以${\theta }_j$$对{\varphi }_i$的求导就有两种情况，i=j 和 i!=j, i=j时，计算结果就是红框4所处的公式，i!=j时就是红框3的公式，可以看到这两个公式中都出现了二阶的偏导，二阶偏导求起来比较麻烦会影响到计算速度，所以作者使用了一阶近似的方法 first-order approximation，也就是把公式中的二阶偏导近似为0，这样近似后就简单很多，即${\theta }_j$$对{\varphi }_i$的求导在i=j时约等于1，在 i!=j 时约等于0。然后顺着图中的蓝色箭头一步步带入，最后就会得到$l(\hat{\theta })$对$\varphi$的求导近似等于$l(\hat{\theta })$对$\hat{\theta }$的求导，再回到更新 meta 参数的公式来看就简单了：

上图红框标出的公式就是 meta 更新参数时实际做的事情，这个式子可以这样看 $((\varphi -\beta \ast g_1)-\beta \ast g_2)-\beta \ast g_3-....$，这是什么意思呢？$g_i$是第 i 个任务在其测试集上计算出的梯度方向，从几何上看，这个式子的更新过程是这样的：

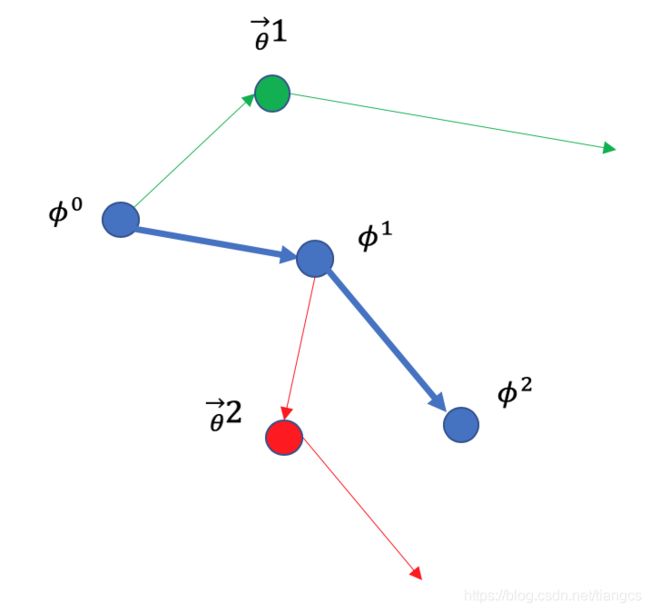
蓝色点表示网络模型真正的参数，绿色第一个箭头表示在其训练集 D 上计算的梯度，绿色第二个箭头表示在其测试集 $D^{\prime }$上计算出的梯度，蓝色箭头表示 meta 模型网络模型参数的方向，可以看到它就是在每个任务的测试集的梯度方向上不断的去做更新。从这个过程中可以看出来，MAML 真正更新网络模型参数时，关心的是测试集上的梯度，而不是每个任务上训练集的梯度，也就是说，它更新的每一步的目标，都是使得更新后的参数能在以后的测试集上表现的更好，正是因为这样，才能说明 meta 停止更新时的参数具有很好的潜力/学习能力，这个能力使得这组参数在之后新的任务上微调几次就可以在该任务上取得很好的性能，当然理想情况还是微调一次就能取得不错的成绩，如果一次微调更新效果不好，那还可以再继续多次的微调更新。这也与我们最初希望的目标，即能在新任务上快速适应相吻合，即使该任务只有少量的训练样本，比如10条或者5条，甚至是1条样本，也能快速的学习到一些有效特征。

first-order approximation 疑问

在看上面的公式的时候，楼主有一个疑问，就是红框3和红框4标注的位置，作者把这个式子近似等于0，并称之为 first-order approximation一阶近似。这个二阶偏导式子是 $\hat{\theta }$ 由 $\varphi$经过一次梯度下降更新推导过来的，如果 $\hat{\theta }$是经过两次或者多次梯度下降更新得到，那么这个式子会不会出现三阶甚至更高阶偏导，如果是的话那还能用近似的方式吗？

带着这个疑问，搜了搜作者 GitHub 的 issue，还真搜到了有人问类似的问题，

作者解答说，即使进行多次梯度下降更新，这里也只会出现二阶偏导。只恨自己数学太渣，理解不了，哪位数学大佬可以推导下的，麻烦私信我下，哈哈，在此先行谢过。

和迁移学习的区别

前面讲过，元学习和迁移学习有相似的地方，形式上都是在之前的任务上进行预训练，然后获得一组参数，然后用这组参数在新的任务继续微调，但它们是有本质的区别的。想想迁移学习的预训练是怎么训练的，比如在 ImageNet 大数据集上预训练的 RestNet、VGG 这些网络模型，它们在训练的时候是用在 ImageNet 训练集上的 loss 算出来的梯度来更新模型参数的，以训练集上的 loss 为准，关心的是当前模型参数在训练集上的性能如何。而元学习 MAML 在训练期间是用测试集上的 loss 算出的梯度来更新模型参数的，以测试集上的 loss 为准，不关心在当前训练集上的性能，而是关心这组参数在之后的测试集上的性能如何，也就是这组参数的潜力。换句话说，在 MAML 这篇论文中，是看这组参数在更新一次后的模型参数在测试集上能够表现多好，而不是训练期间能够多好，这种潜力也与元学习的大目标相符，即 Learn to learn 学会如何学习从而具备某种学习能力或学习技巧，可以在新的任务上快速学习。类比到上面老师和学生的例子，也很好理解，老师每次都是以学生的平均考试成绩为方向进行调整，这个考试成绩自然是每门功课上没有见过的题目，只有这样才能训练出该学生的学习能力。

从几何上来看，迁移学习预训练模型的参数更新过程是这样的：

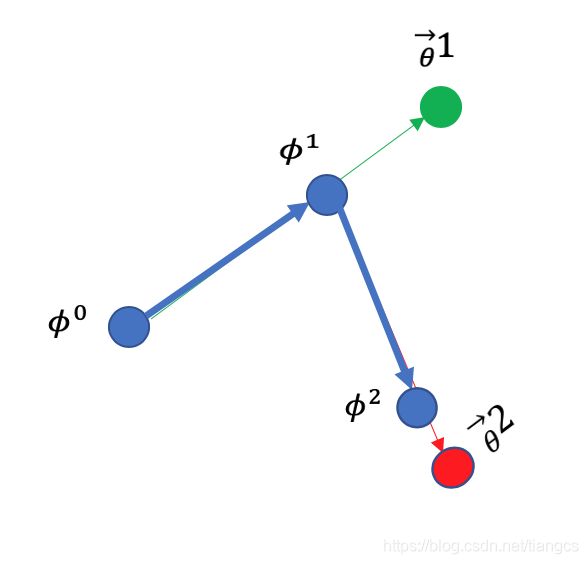
这就能看出和 MAML 不一样的地方了，迁移学习的预训练每次更新参数时，都是在当前任务上训练集的梯度方向上进行更新。

论文实验

上面详细讲了论文的思想及数学过程，下面来看下论文中的一些实验及结论。论文中的所有实验都是少样本学习的场景，因为少样本学习是元学习一个典型的应用场景，元学习在少样本上也更能发挥出它的威力。

回归问题

论文中关于回归问题的例子是，拟合正弦函数曲线，所有任务的分布p(T)就是正弦函数分布 y=a*sin(x+b)，不同的任务只需要抽样不同的 a和b 即可，按照上面讲的 MAML 训练过程，在若干个不同 a和b 的正弦函数上进行预训练，然后用预训练出的网络模型在新的正弦函数样本上进行测试，这个新的正弦函数是训练期间没有见过的一组a和b，只给出少量的训练样本，如5个或10个。论文中对比了 MAML 模型和迁移学习预训练模型，在这个新的正弦函数上的预测性能，注意不管是哪种模型在这个新的任务上都还是要进行训练的，只不过这个训练是在之前参数的基础上微调，这个新任务对于 meta 来说就是推理任务，而在任务内部还是需要微调更新的。下图就是 MAML 模型和预训练模型在新的正弦函数上训练之后，在其测试集上的表现。

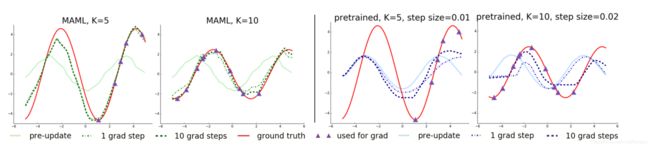
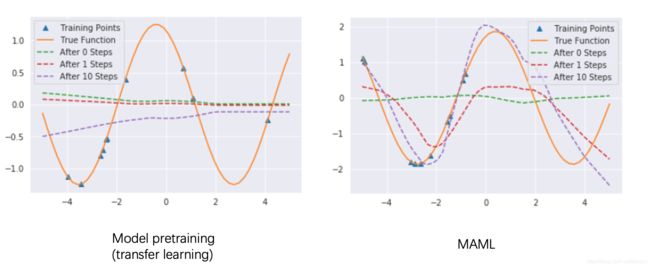
左边两个图是 MAML 模型的结果，左边第一个图是用 MAML 的思路训练出的模型，在新正弦函数的 5 个样本上微调之后，进行预测的结果。可以看到新的正弦函数，在训练时只给了分布在右半部分的 5 个点，其中红色线是真实分布，浅绿色线是不进行微调直接用预训练参数进行预测的结果，可以看出来预训练参数跑出的结果已经有了初步的形状。深绿色线是微调一次参数后进行预测的结果，此时预测出的曲线已经基本拟合真实的正弦函数了，在包含训练样本的右半侧可以完全拟合，在左半边的曲线，模型虽然没有见过这部分的样本但也可以学习出它的周期性质，在形状上基本拟合。左边第二个图不同的是，给出了新的正弦函数的10个训练样本，可以看到 MAML 在进行一次微调后，基本就可以拟合全部曲线了，在进行十次微调后，拟合程度更进一步。

右边两个图是同样的设置下，迁移学习预训练模型的表现，浅蓝色曲线是直接进行预测的结果，可以看到和真实分布相差甚远，尤其是波峰的位置，完全没对上，在微调1次和10次之后，相比于不微调，有一点进步，但和真实分布相比，依然相差较大。并且模型发生了过拟合现象，如果样本点只在右半部分，那模型在右半部分的拟合上表现还行，在另一半的位置上表现更差。如果迁移学习预训练的任务足够多的话，它训练出的模型对应的曲线应该是一条接近水平的直线，因为每个任务都以训练集上的 loss 为主，这么多任务的 loss 加起来更新参数时，梯度应该接近于0。从几何上理解就是，很多个正弦函数叠加在一起，其趋势就是一个水平线，同一个点，可能是波峰也可能是波谷，中间水平线的位置才能让所有任务上的 loss 最小，这就是迁移学习预训练和元学习的质的差别。

上面的图可能不是很明显，有第三方的作者复现了这个回归实验，并且重新绘制了这部分的图，如下所示，这个图看起来更明显些。

论文中也对微调次数进行了实验，结果如下图：

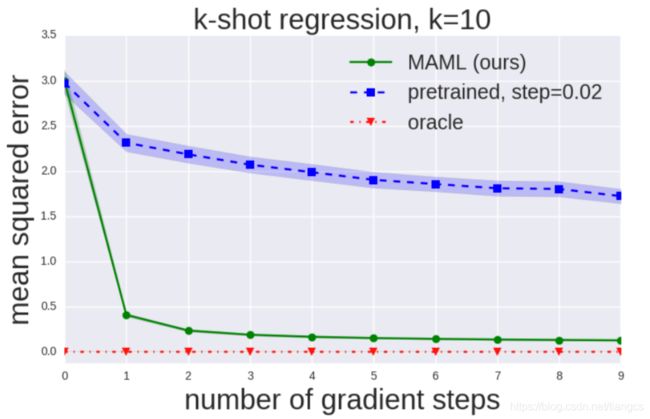
红色线是 oracle 设置组的结果，oracle 就是在训练时加入了该任务真实的a和b作为特征，相当于提前知道了真实分布，所以在这个设置下训练的模型，在新任务上的 mse loss 基本为 0 ，绿色线是 MAML 的模型，横轴是微调次数，可以看到微调一次的模型，就可以得到很低的 mse 误差，而随着微调次数增加，性能也逐渐提升，不过由微调1次变为2次，提升还比较明显，后面的提升就不明显了，尤其是在5次微调之后，基本就没有提升了。蓝色线是迁移学习的预训练模型，可以看到不管是微调几次，其 mse 值都很大，与 MAML 的模型相比，更是相差甚远。

分类问题

分类问题场景是两个少样本学习中常见的基准数据集：MiniImagenet 和 Omniglot，下图是在 Omniglot 数据集上的结果：

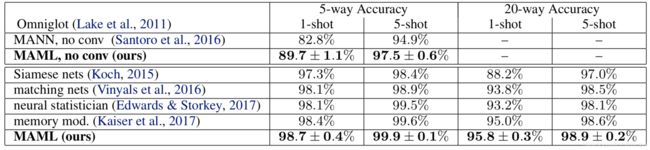
其中 5-way 是表示5分类，1-shot 表示训练时每个类别下只有一个样本，5-shot就是每个类别下只有5个样本，可以看到不管在哪个设置下，MAML 模型的表现都是最好的。

下图是在 MiniImagenet 数据集上的结果：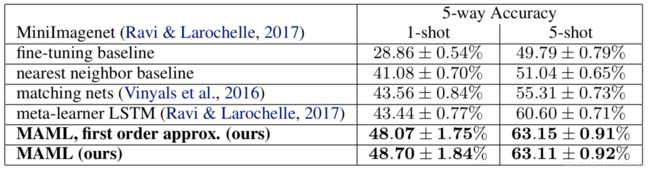
在这个数据上，作者还对比了使用一阶微分近似和不使用的结果，还记得一阶微分近似是啥吗？不记得的话，请往上翻看数学公式部分，可以看到使用了一阶微分近似，在效果上相差不大，但是作者证明在速度上可以提高 33% 左右，这可是一个性价比很高的改进。

参考资料

1. MAML 论文
2. MAML github
3. https://github.com/AdrienLE/ANIML/blob/master/ANIML.ipynb
4. B站杨弘毅 meta-learning 部分视频： https://www.bilibili.com/video/BV1Gb411n7dE?p=32
5. https://cs330.stanford.edu/