机器学习算法----决策树与随机森林 (信息熵、信息增益率、剪枝、OOB) (学习笔记)
文章目录
- 决策树
-
- 熵、信息熵、信息增益:
- 剪枝
- 随机森林
-
- OOB (袋外错误率)
- 学习参考
前两天整理的笔记:
- 支持向量机 SVM
- 各种聚类算法
今天整理一下决策树和随机森林。
决策树
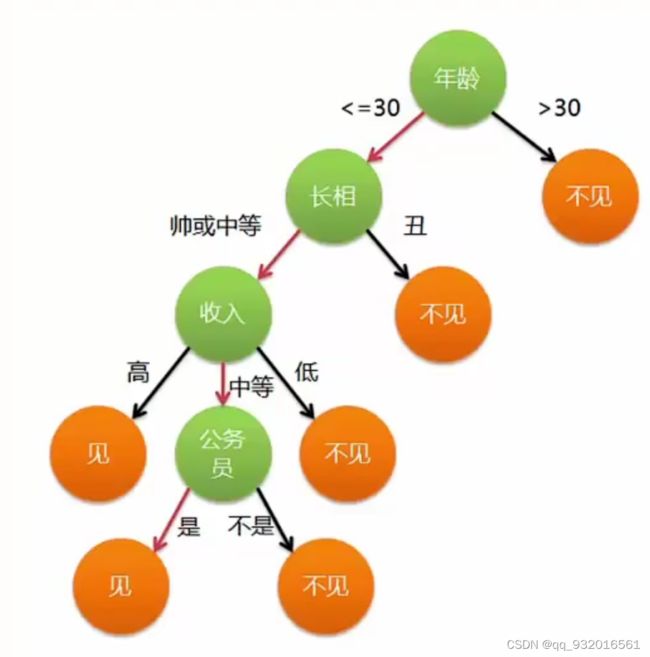
决策树顾名思义,一张图解释一下:
假设要见相亲对象,看这张图,这就是决策树的大概过程,每一个非叶子节点都是条件,叶子节点是结果,分支就是条件。
熵、信息熵、信息增益:
这俩东西的原理和计算方法后面再说了,一句话理解:
可以理解为混乱程度(分类效果不好)。
比如分类结果A里面啥都有,则他的混乱程度较大,所以熵值就大。
构造决策树的基本思想:随着深度的增加,节点的熵迅速的降低。熵降低的越快越好,希望得到一颗高度尽量矮的决策树。
说一下熵(信息熵)的计算方法,公式:
Gini系数计算公式:
对于一开始给的那张图,为什么第一个根节点是年龄呢?实例中用谁当根节点是怎么确定的?
用一个例子来说:
假如有如下数据,每一列数据:天气 ,温度,湿度,风。最后一列play就是代表这样的天气是否出去玩,相当于lable。
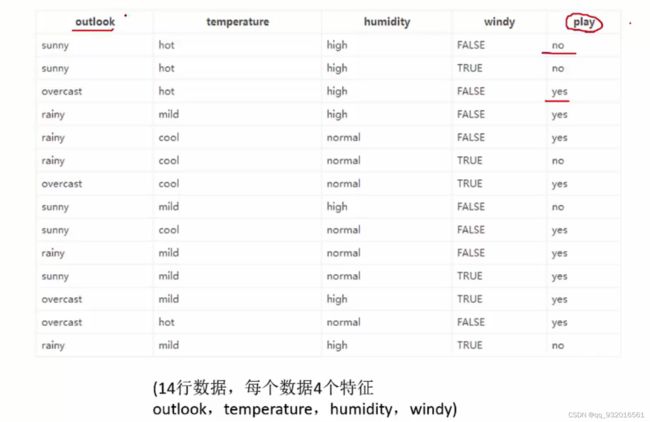
这其中结果列 play(lable),一共有5个no,9个yes。所以出去玩的概率 9/14, 不出去玩的概率5/14。
我们的数据中有很多特征,比如天气 ,温度,湿度,风。用上面计算的方法分别计算出来这四个特征的熵。
比如:outlook分别取sunny、overcast、rainy概率分别是5/14、4/14、5/14,所以:
![]()
可以看到,如果让outlook当根节点的话,熵变成0.693,比刚才的0.940低了0.247.熵变低,说明结果混乱程度变低,纯度变高,分类效果变好。
这里有个概念:
信息增益(gain) = 0.940-0.693 = 0.247
同样计算出其他的特征的信息增益,gain(temperature) = 0.029 ,gain(humidity) = 0.152 ,gain(windy) = 0.048.
gain(outlook)最大,则说明使用outlook当根节点在第初始的时候使得系统的熵下降的最快,所以决策树选择outlook当根节点。
几种构建决策树的算法。
- ID3:信息增益
- C4.5: 信息增益率 (ID3扩展算法)
- CART:Gini系数
- 评价函数,类似于损失函数。
信息增益率在信息增益的基础上增加了惩罚项,惩罚项是特征的固有值。
信息增益率=信息增益/自身的熵值。
剪枝
为了得到尽可能矮的树,引入剪枝操作:
- 预剪枝:在构建决策树的过程中,提前停止。(边造边剪)
- 后剪枝:决策树建立好后才开始剪枝。 (造完再剪)
在后剪枝的时候,引入一个损失函数来判断那些需要剪枝,
损失评价函数:
随机森林
随机森林就是通过集成学习的Bagging思想将多棵树集成的一种算法。
随机森林 = N个变异决策树
这里的是变异决策树,不同于上面的决策树,这里的变异决策树不再使用全部特征和全部样本,而是随机使用部分特征和样本(有放回的随机采样bootstrap sample),这里其实很好想,一般的数据都是有很多噪点的,每次使用随机的部分特征和样本构建决策树时,会有一部分树选择的特征或样本里没有噪点,这样就能得到比较好的结果。
OOB (袋外错误率)
如何随机 是随机森林的一个主要问题。
要解决这个问题主要依据计算袋外错误率OOB error(out-of-bag error)。
在构建每棵树时,我们对训练集使用了不同的bootstrap sample(随机且有放回地抽取)。所以对于每棵树而言(假设对于第k棵树),大约有1/3的训练实例没有参与第k棵树的生成,它们称为第k棵树的oob样本。而这样的采样特点就允许我们进行oob估计,它的计算方式如下:
- 对每个样本,计算它作为oob样本的树对它的分类情况(约1/3的树);
- 然后以简单多数投票作为该样本的分类结果;
- 最后用误分个数占样本总数的比率作为随机森林的oob误分率。
学习参考
决策树:https://blog.csdn.net/weixin_39913422/article/details/111664969
信息熵:https://blog.csdn.net/qq_35509823/article/details/104705345
袋外错误率:https://zhuanlan.zhihu.com/p/406627649
视频教程:https://www.bilibili.com/video/BV19R4y1F7af?p=8&spm_id_from=333.337.top_right_bar_window_history.content.click

