李宏毅机器学习课程笔记-1|CSDN创作打卡
李宏毅机器学习课程笔记
文章目录
- 李宏毅机器学习课程笔记
- 前言
- 一、机器学习是什么?
- 二、如何找到这个方程
-
- 1.写出一个,带有未知参数的函式
- 2.定义一个损失函数
- 3.寻找最好的参数
- 4.如何做的更好一些
- 总结
前言
李宏毅2021春机器学习课程笔记
第1篇
一、机器学习是什么?
机器学习概括来说可以用一句话来描述机器学习这件事,机器学习就是让机器具备找一个方程的能力。

二、如何找到这个方程
机器学习找这个函式的过程,分成三个步骤
- 写出一个,带有未知参数方程
- 定义一个东西叫做Loss
- 解一个最佳化
我们用Youtube频道,点阅人数预测这件事情,来跟大家说明这三个步骤,是怎么运作的
1.写出一个,带有未知参数的函式
简单来说就是 我们先猜测一下,我们打算找的这个函式,它的数学式到底长什么样子。比如对于Youtube频道点阅人数的预测,猜测一个简单的一次函数:
y=w*x+b
y是我们要预测的东西
x是输入
w、b都是未知的参数
2.定义一个损失函数
对于我们预测的方程以及其参数,我们需要一个方程来说明这个方程是否符合我们的预期。简单来说,对于上面的y=wx+b,我们就可以用预测的Y和真实的Y做差然后取绝对值来表示二者之间的差距,就是loss的值,也就是这个参数的好坏。
3.寻找最好的参数
那我们如何寻找一个最小的值来让这个loss最小呢?
如果我们只关注其中的一个参数变量,其余的都不动。那这个问题就是找一个函数的最小值的问题,当一阶导数为0时,我们可以找到极值点。在我们没有一个具体的函数时,我们可以先定义一个初始点,然后求该点的微分,也就是该点对应的斜率,然后根据这个斜率来判定接下来是向什么方向走才能接近图像的下方,重复这个步骤直到微分为0.显然,对于一个函数来说极值点可能不止一个,那这个方法可能只能得到一个local minima,并非全局最优解。
但对于这个问题老师的原话是:事实上,假设你有做过深度学习相关的事情,假设你有自己训练network,自己做过Gradient Descent 经验的话,其实local minima是一个假问题,我们在做Gradient Descent 的时候,真正面对的难题不是local minima,到底是什麼,这个 我们之后会再讲到,在这边你就先接受,先相信多数人的讲法说,Gradient Descent,有local minima的问题,在这个图上在这个例子裡面,显然有local minima的问题,但之后会再告诉你说,Gradient Descent真正的痛点,到底是什麼。

4.如何做的更好一些
以上的预测都是我们用已经有的真实数据做预测,那实际上的预测结果怎么样呢?

观察这个结果,我们可以发现预测的结果几乎就是前一天的数据。事实上,在训练资料上的loss是0.45k,实际预测是是0.58k的误差。另外,我们可以注意到这个数据似乎是有规律的,它会周期性地上升下降,那如果我们将这个周期考虑进去,比如用七点的值做预测那结果或许会更好。
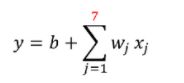
然后我们获得了更低的loss,是0.38k,在真实的预测时也有比较好,是0.49k。
总结
我们研究的很多模型都是线性系统。
线性系统有个定义,个人简单理解就是:
1.
就是k倍的输入,其输出也要是k倍。
2.
不同的输入之间满足叠加原理。
满足以上两个条件的系统就是线性系统
比如y=kx,积分,微分,矩阵的转置等
而y=x^2就不是。
常见的电路里,电阻,电感,电容也都是线性系统,由他们组成的电路也是线性系统。